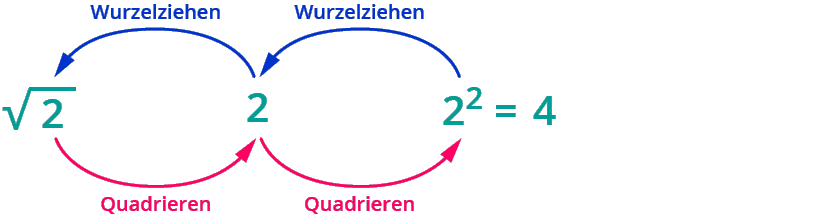
Potenzgesetze / Wurzelgesetze
Rechenregeln für Potenzen
Erinnerst du dich noch an die Potenzgesetze?
1. Potenzgesetz
$$a^m*a^n=a^(m+n)$$
$$a^m/a^n=a^(m-n)$$ mit $$a !=0$$
2. Potenzgesetz
$$a^n*b^n=(a*b)^n$$
$$a^n/b^n=(a/b)^n$$ mit $$b !=0$$
3. Potenzgesetz: Potenzen potenzieren
$$(a^n)^m=a^(n*m)$$
Bisher hast du für $$m$$ und $$n$$ ganze Zahlen eingesetzt.
Die Potenzgesetze gelten aber auch für Brüche im Exponenten! Mathematisch genau: wenn die Exponenten rationale Zahlen sind.
Die Gesetze gelten, wenn $$m, n in QQ$$.
Die Potenzgesetze gelten nicht nur für Exponenten aus den ganzen Zahlen $$ZZ$$, sondern für Exponenten aus den rationalen Zahlen $$QQ$$.
Ganze Zahlen $$ZZ$$ sind $$ZZ={…-3;-2;-1;0;1;2;3;…}$$
Die rationalen Zahlen $$QQ$$ sind positive und negative Brüche:
$$QQ={p/q | p, q in ZZ; q !=0}$$
Beispiele
1. Potenzgesetz
Vereinfache. Rechne so viel wie möglich ohne Taschenrechner.
$$2^(1/3)*2^(2/3)=2^(1/3+2/3)=2^1=2$$
$$144^(-3/2)*144^2=144^(-3/2+4/2)=144^(1/2)=sqrt144=12$$
$$(x^(11/4))/(x^(3/4))=x^(11/4-3/4)=x^(8/4)=x^2$$
2. Potenzgesetz
$$4^(1/2)*16^(1/2)=(4*16)^(1/2)=64^(1/2)=8$$
$$(32^(3/4))/(2^(3/4))=(32/2)^(3/4)=16^(3/4)=8$$
3. Potenzgesetz: Potenzen potenzieren
$$(3^(1/2))^4=3^(1/2*4)=3^2=9$$
$$(49^(1/6))^(-3)=49^(1/6*(-3))=49^(-3/6)=49^(-1/2)=1/(49^(1/2))=1/sqrt49=1/7$$
Und wie sieht’s mit Wurzeln aus? Kannst du die Gesetze auf $$n$$-te Wurzeln übertragen?
Für das 1. Potenzgesetz gibt es keine Entsprechung bei den Wurzeln, aber für die anderen zwei!
Zur Erinnerung:
1. Potenzgesetz:
$$a^m*a^n=a^(m+n)$$
$$a^m/a^n=a^(m-n)$$ mit $$a !=0$$2. Potenzgesetz
$$a^n*b^n=(a*b)^n$$
$$a^n/b^n=(a/b)^n$$ mit $$b !=0$$3. Potenzgesetz: Potenzen potenzieren
$$(a^n)^m=a^(n*m)$$
Die $$n$$-te Wurzel aus einem Produkt
Versuche, mithilfe der Potenzgesetze Wurzelterme umzuformen.
Beispiel:
$$sqrt(4)*sqrt(9) stackrel(?)=sqrt(4*9)$$
Los geht’s mit $$sqrt(4)*sqrt(9) $$
Umwandeln in Potenzen:
$$sqrt(4)*sqrt(9)=4^(1/2)*9^(1/2)$$
Anwenden des 1. Potenzgesetzes:
$$4^(1/2)*9^(1/2)=(4*9)^(1/2)$$
Umwandeln in eine Wurzel:
$$(4*9)^(1/2)=sqrt(4*9)$$
In Kurzform:
$$sqrt(4)*sqrt(9)=4^(1/2)*9^(1/2)=(4*9)^(1/2)=sqrt(4*9)$$
Das wolltest du zeigen.
Diese Rechnung kannst du für alle möglichen Zahlen, also auch allgemein für Radikanden $$a$$ und $$b$$ und Exponenten $$n$$ durchführen. (Die Radikanden dürfen natürlich nicht negativ sein.)
Willst du n-te Wurzeln multiplizieren, multipliziere die Radikanden. Die Wurzel bleibt gleich.
$$root n(a)*root n(b)=root n(a*b)$$ für jede natürliche Zahl $$n$$,
$$a,$$ $$b ge0$$
Zur Erinnerung:
2. Potenzgesetz
$$a^n*b^n=(a*b)^n$$
$$a^n/b^n=(a/b)^n$$ mit $$b !=0$$$$root n(x)=x^(1/n)$$
Zur Kontrolle:
$$sqrt(4)*sqrt(9)=2*3=6$$
$$sqrt(4*9)=sqrt(36)=6$$

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Und die Division?
Wie mit Produkten kannst du dir auch die Regel zur Wurzel aus Quotienten überlegen.
Beispiel 1:
$$root 4 (16)/root 4 (81)=16^(1/4)/81^(1/4)=(16/81)^(1/4)=root 4 (16/81)$$
Beispiel 2:
Andersum ist es manchmal praktisch zum Rechnen: $$root 4 (16/81)=root 4 (16)/root 4 (81)=2/3$$
Willst du n-te Wurzeln dividieren, dividiere die Radikanden. Die Wurzel bleibt gleich.
$$root n (a)/root n (b)=root n (a/b)$$ für jede natürliche Zahl $$n$$,
$$a ge0$$ und $$b >0$$
Zur Erinnerung:
2. Potenzgesetz
$$a^n*b^n=(a*b)^n$$
$$a^n/b^n=(a/b)^n$$ mit $$b !=0$$$$root n(x)=x^(1/n)$$
Die Wurzel in der Wurzel
Untersuche die letzte Rechenregel: Was passiert, wenn du die Wurzel aus einer Wurzel ziehst?
Beispiel:
$$root 2(root 5 (59049))=(59049^(1/5))^(1/2)=59049^(1/10) = root 10 (59049)$$
Also: $$root 2(root 5 (59049)) = root (2*5) (59049)$$
Und allgemein:
Willst du eine Wurzel aus einer Wurzel ziehen, multipliziere die Wurzelexponenten.
$$root m(root n (a))=root (m*n) (a)$$ für natürliche Zahlen $$n$$ und $$m$$
$$a>=0$$
Zur Erinnerung:
Potenzen potenzieren:
$$(a^n)^m=a^(n*m)$$$$root n(x)=x^(1/n)$$
Beispiele
$$root 4 (162)*root 4 (8)=root 4 (162*8)=root 4 (1296)=6$$
$$(root 6(5))/(root 3 (5))=root6 5 *1/(root3 5)=5^(1/6)*5^(-1/3)=5^(1/6-1/3)=5^(-1/6)=1/root6 5$$
$$root 12(64)=root(3*4) (64)=root 4(root 3 (64))=root 4 (4)=root (2*2) (4)=sqrt(sqrt4)=sqrt2$$
Nicht durcheinanderkommen: $$sqrt( )$$ ist die 2. Wurzel, nicht etwa die 1. :-)
Die Wurzelgesetze
- $$root n(a)*root n(b)=root n(a*b)$$
$$n in NN,$$ $$a,$$ $$b ge0$$ - $$root n (a)/root n (b)=root n (a/b)$$
$$n in NN$$, $$a ge0$$ und $$b >0$$ - $$root m(root n (a))=root (m*n) (a)$$
$$m,n in NN,$$ $$a>=0$$

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen