Potenzgleichungen lösen
Bevor es losgeht
Für Potenzgleichungen solltest du gut mit Potenzen und Wurzeln umgehen können. Hier kommen die wichtigsten Dinge in der Übersicht, dann kannst du Potenzgleichungen auch gut lösen.
Was ist eine Potenz?
Multiplizierst du eine Zahl mehrfach mit sich selbst, kannst du das Produkt als Potenz schreiben.
$$5*5*5*5=5^4$$
└──┬───┘
$$4$$-mal der Faktor $$5$$
Exponent oder Hochzahl
$$uarr$$
$$5^4=625$$
$$darr$$ $$darr$$
Basis Potenzwert
Als Basis kannst du auch Bruch- und Dezimalzahlen sowie reelle Zahlen verwenden:
$$cdot$$ $$(2/5)^2=(2/5)*(2/5)=4/25$$
$$cdot$$ $$(-0,3)^3=(-0,3)*(-0,3)*(-0,3)=-0,027$$.
Der Exponent (Anzahl der Faktoren) ist eine natürliche Zahl.
Die Potenz $$a^n$$ der reellen Zahl $$a$$ und der natürlichen Zahl $$n$$ ist das Produkt $$a*a*…*a$$ aus $$n$$ Faktoren. Die Berechnung der $$n$$-ten Potenz einer Zahl $$a$$ heißt Potenzieren.
Mit Potenzen kannst du rechnen! Potenzen mit gleicher Basis kannst du multiplizieren, indem du die Exponenten addierst. Beispiel: $$10^3*10^2=10^(3+2)=10^5$$
Was ist eine Wurzel?
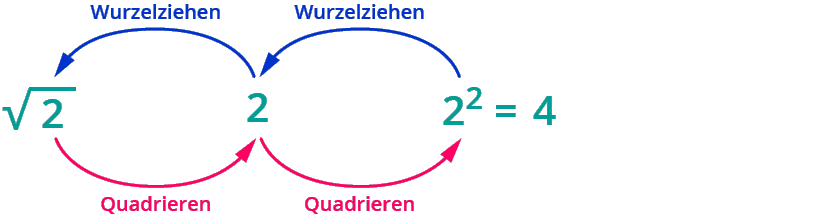
Das Wurzelziehen ist die Umkehrung vom Potenzieren.
Welche Zahl „hoch 4“ ergibt 625? Dazu brauchst du die Wurzel:
- $$root 4 (625)=5$$, denn $$5^4=625$$
- $$root 3 (8)=2$$, denn $$2^3=8$$
Das Wurzelziehen ist die Umkehrung zum Potenzieren.
Begriffe:
Wurzelexponent
$$uarr$$
$$root 3 (8)=2$$ $$rarr$$ Wurzelwert
$$darr$$
Radikand
Die $$n$$-te Wurzel $$root n (b)$$ der positiven reellen Zahl $$b$$ und der natürlichen Zahl $$n$$ ist die positive Zahl $$a$$, für die gilt $$a^n=b$$. Die Berechnung der $$n$$-ten Wurzel einer Zahl $$a$$ heißt Radizieren und ist die Umkehroperation zum Potenzieren.
1. Der Wurzelwert ist immer positiv. Es ist zwar auch $$(-5)^4=625$$ und es könnte $$ root 4 (625) =-5$$ sein. Aber das Wurzelziehen muss eindeutig sein, sonst gäbe es „sinnlose“ Rechnungen wie z.B.
$$root 4 (625) + root 4 (625) = 5 + (-5)=0$$.
Also $$root 4 (625)!=-5$$!2. Der Radikand ist immer positiv (oder $$0$$) Es ist zwar $$(-2)^3=-8$$ und es könnte $$root 3 (-8)=-2$$ sein. Aber: Wurzeln kannst du auch als Potenzen mit Brüchen als Exponenten betrachten, z. B. $$root 3 (8)=8^(1/3)$$ Somit wäre die widersprüchliche Rechnung möglich: $$-2=root 3 (-8)=(-8)^(1/3) =(-8)^(2/6)$$ $$=(-8)^(2*1/6)=root 6 ((-8)^2)=root 6 (64)=2$$ mit $$-2!=2$$.
Also: Keine negativen Radikanden!
Potenzgleichungen
Jetzt bist du fit, um Gleichungen mit Potenzen zu lösen.
Gleichungen der Form $$x^n=b$$ mit natürlichen Zahlen $$n, n >=1,$$ und reellen Zahlen $$b$$ heißen Potenzgleichungen.
Alle reellen Zahlen $$x$$, die die Gleichung erfüllen, sind Lösungen der Potenzgleichung.
Beispiel: $$x^3=27$$
Die Lösung ist $$x=3$$, da $$3^3=27$$.
Oder mit Umformung geschrieben:
$$x^3=27$$ | $$root 3 ( )$$
$$x=root 3 (27)=3$$
$$x=3$$
Potenzgleichungen haben die Form $$x^n=b$$ mit $$n in NN$$ und $$n>=1$$. Alle reellen Zahlen $$a$$ mit $$a^n=b$$ sind Lösungen der Potenzgleichung.
In Potenzgleichungen der Form $$x^n=b$$ musst du zu gegebenem natürlichen Exponenten $$n$$ und zu reellem Potenzwert $$b$$ die Basis einer Potenz bestimmen.
Für $$n=2$$ erhältst du einfache quadratische Gleichungen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Potenzgleichungen $$x^n=b$$ lösen
Für $$x^n=0$$ ist das schnell gemacht. Dann gibt es nur die Lösung $$x=0$$ für alle $$n$$, denn $$0^n=0$$ für alle natürlichen Zahlen $$n$$.
Für $$b!=0$$ unterscheidest du zwischen Potenzgleichungen mit geraden und mit ungeraden Exponenten.
Potenzgleichungen mit geraden Exponenten
Die Potenzgleichung $$x^n=b$$ mit geradem $$n$$ hat nur dann eine Lösung, wenn $$b>=0$$, z. B. $$x^2!=-4$$ für alle $$x$$.
Beispiel 1 Gleichung: $$x^4=81$$ Radizieren auf beiden Seiten: $$root 4 (x^4)=root 4 (81) rArr x=3$$ Lösungen: $$x_1=3$$ und $$x_2=-3$$, denn $$3^4=(-3)^4=81$$
Beispiel 2 Gleichung: $$x^4=56$$ Radizieren auf beiden Seiten: $$root 4 (x^4)=root 4 (56) rArr x=root 4 (56)$$ Lösungen: $$x_1=root 4 (56) approx 2,74$$ und $$x_2=-root 4 (56) approx -2,74$$
Potenzgleichungen $$x^n=b$$ mit geraden natürlichen Zahlen $$n$$ haben für $$b in RR$$ und $$b<0$$: keine Lösung, $$b=0$$: eine Lösung $$x=0$$,
$$b>0$$: zwei Lösungen $$x_1=root n (b)$$ und $$x_2=-root n (b)$$.
Potenzen mit geraden Exponenten sind immer positiv.
Für alle $$n in NN$$ ist $$0^n=0$$.
Der Wert einer Wurzel $$root n (a)$$ ist immer positiv.
Potenzgleichungen mit ungeraden Exponenten
Die Potenzgleichung $$x^n=b$$ mit ungeradem $$n$$ hat für alle reellen Zahlen $$b$$ eine und nur eine Lösung.
1. Fall: $$b>0$$Beispiel $$x^3=125$$ | $$root 3( ) $$ $$rArr$$ $$x= root 3 (125)=5$$
Lösung: $$x=5$$, denn $$5^3=125$$
2. Fall: $$b<0$$Beispiel $$x^3=-64$$ Hilfsschritt: Gleichung mit positivem $$b$$ lösen:
$$x^3=64$$ | $$root 3 ( )$$ $$rArr$$ $$x= root 3 (64)=4$$
Lösung ursprüngliche Gleichung: $$x=$$ $$-$$ $$4$$, denn $$(-4)^3=(-4)*(-4)*(-4)=-64$$.
Potenzgleichungen $$x^n=b$$ mit ungeraden natürlichen Zahlen $$n$$ haben für alle $$b in RR$$ eine Lösung und die Lösung für $$b<0$$: $$x=-root n (-b)$$, $$b=0$$: $$x=0$$,
$$b>0$$: $$x=root n (b)$$.
Für $$b<0$$ (2. Fall) kannst du nicht einfach auf beiden Seiten die $$n$$-te Wurzel ziehen, da die Wurzel nur aus nicht-negativen Zahlen gezogen werden kann. Die Wurzel $$root n (b)$$ ist für $$b<0$$ nicht definiert.
„Erweiterte“ Potenzgleichungen
Manche Gleichungen kannst du durch äquivalente Umformungen in die Form $$x^n=b$$ überführen.
Beispiel $$2x^3-4=-10$$
1. Äquivalente Umformung
$$2x^3-4=-10$$ $$|+4$$
$$2x^3=-6$$ $$|:2$$
$$x^3=-3$$
2. Lösen der Potenzgleichung mit $$b<0$$ Hilfsschritt: Gleichung mit positivem $$b$$ lösen:
$$x^3=3$$ | $$root 3( )$$
$$rArr x=root 3 (3) $$
Lösung ursprüngliche Gleichung:
$$x=-root 3 (3) approx -1,44$$
Bringe „erweiterte“ Potenzgleichungen immer erst in die Form $$x^n=b$$ und löse sie dann.
Bei äquivalenter Umformung einer Gleichung ändern sich die Lösungen der Gleichung nicht.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Potenzgleichungen grafisch lösen
Zum grafischen Lösen von Potenzgleichungen der Form
$$x^n=b (b in RR$$ und $$n in NN)$$
bringst du den Graphen einer Potenzfunktion ($$f(x)=x^n$$) und einer linearen Funktionen ($$g(x)=b$$) zum Schnitt.
1. Potenzgleichungen mit geraden Exponenten Potenzgleichung: $$x^2=6,25$$ Lineare Funktion: $$g(x)=6,25$$ Potenzfunktion: $$f(x)=x^2$$
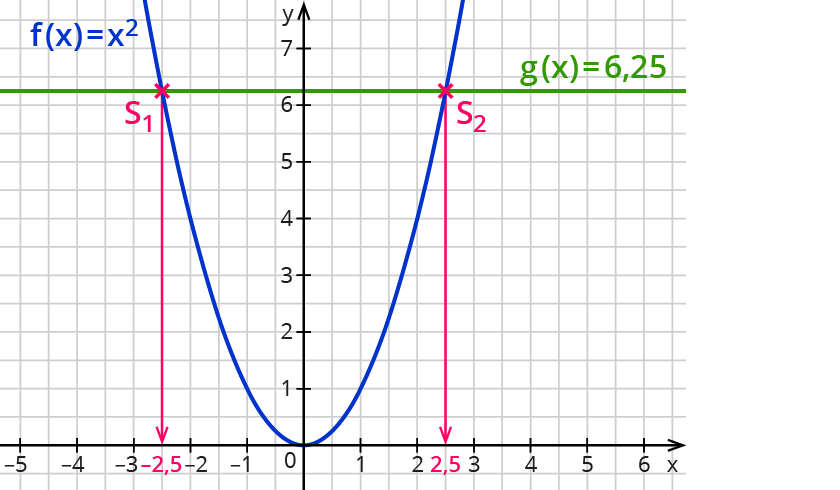
Schnittpunkte der Graphen: $$S_1(-2,5|6,25)$$ und $$S_2(2,5|6,25)$$. Lösungen der Potenzgleichung: $$x_1=-2,5$$ und $$x_2=2,5$$
2. Potenzgleichungen mit ungeraden Exponenten Potenzgleichung: $$x^3=-8$$ Lineare Funktion: $$g(x)=-8$$ Potenzfunktion: $$f(x)=x^3$$
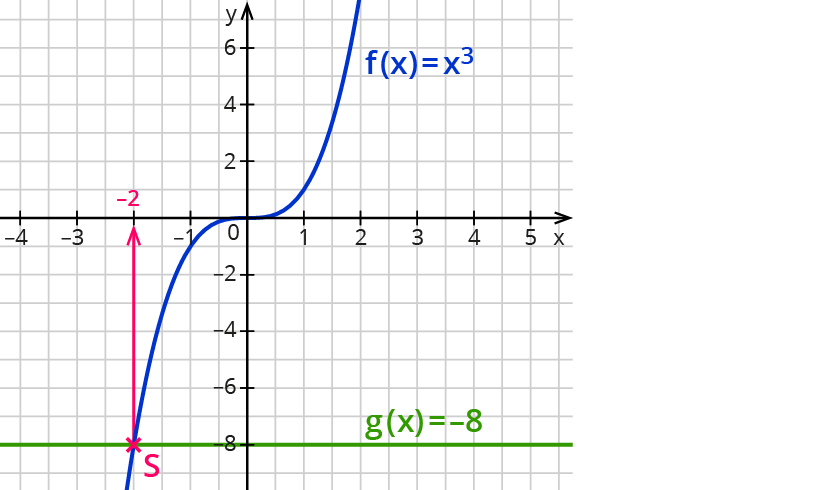
Schnittpunkt der Graphen: $$S(−2|8)$$ Lösung der Potenzgleichung: $$x=−2$$
Potenzgleichungen der Form $$x^n=a$$ kannst du grafisch lösen, indem du die Graphen der Potenzfunktion $$f(x)=x^n$$ und der linearen Funktion $$g(x)=b$$ schneidest. Die $$x$$-Koordinaten der Schnittpunkte sind die Lösungen der Potenzgleichung.
Der Graph der linearen Funktion $$g(x)=b$$ ist eine Gerade parallel zur $$x$$-Achse.
Und jetzt allgemein
Grafisch kannst du schön sehen, wie viele Lösungen Potenzgleichungen $$x^n=b$$ mit geradem und ungeradem Exponenten $$n$$ haben.
1. Potenzgleichungen mit geraden Exponenten
$$f(x)=x^n$$ mit $$n$$ gerade
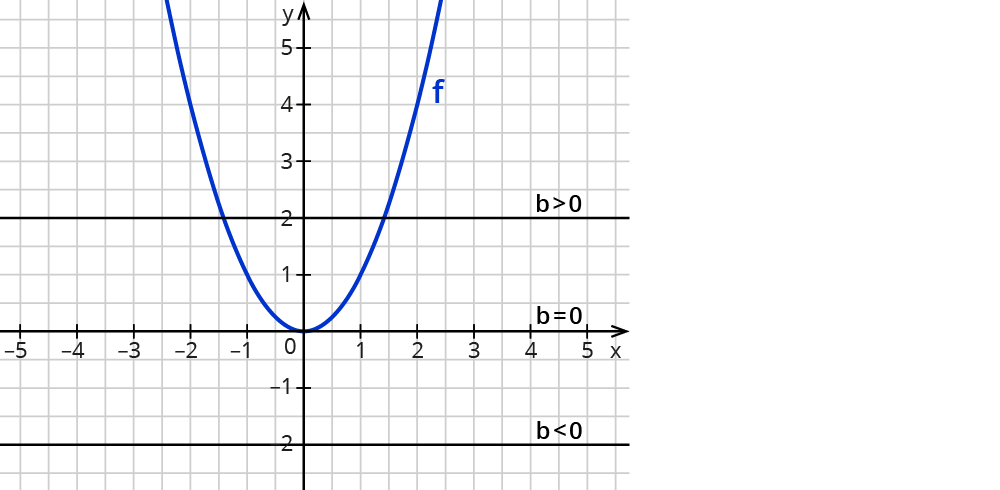
Es gibt entweder keine, einen oder 2 Schnittpunkte. Also keine, eine oder 2 Lösungen der Potenzgleichung.
2. Potenzgleichungen mit ungeraden Exponenten
$$f(x)=x^n$$ mit $$n$$ ungerade

Es gibt immer einen Schnittpunkt der Potenzfunktion mit der Geraden. Also immer eine Lösung der Potenzgleichung.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen