Tangens: Dreiecke berechnen
Berechnungen in beliebigen Dreiecken
Bis jetzt hast du mit Sinus, Kosinus und Tangens nur in rechtwinkligen Dreiecken gerechnet. Diese Beziehungen kannst du auch nur in rechtwinkligen Dreiecken anwenden. Wie kannst du aber in beliebigen Dreiecken ohne rechten Winkel rechnen? Ganz einfach: Erzeuge dir einen rechten Winkel! So geht’s:
Zerlegen
Zerlege dein Dreieck in 2 rechtwinklige Dreiecke. Das geht, indem du die Höhe einzeichnest. Dann kennst du in den Teildreiecken eine Seite und den spitzen Winkel.
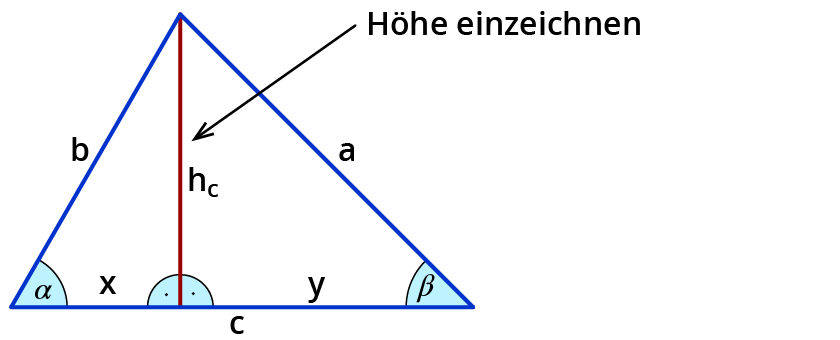
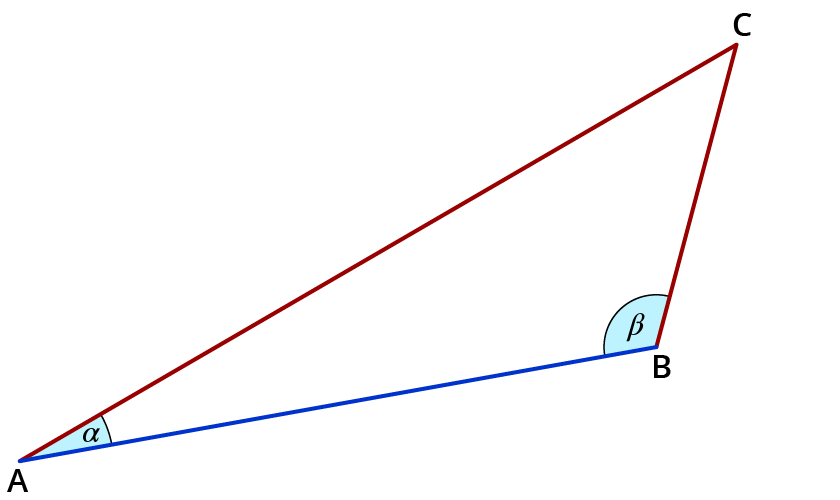
Zerlege das Dreieck, wenn es 3 spitze Winkel hat.
Spitzer Winkel:
$$alpha$$ liegt zwischen $$0^°$$ und $$90^°$$. $$0^° < alpha <90^°$$
Beispielaufgabe Zerlegen
Gegeben ist ein Dreieck mit $$a = 6$$ $$cm$$, $$α = 40^°$$, $$β = 60^°$$. Berechne die Seite $$c$$.
Lösung:
Zeichne die Höhe ein. Die Seite $$c$$ wird so in die Abschnitte $$x$$ und $$y$$ geteilt. $$c=x+y$$.
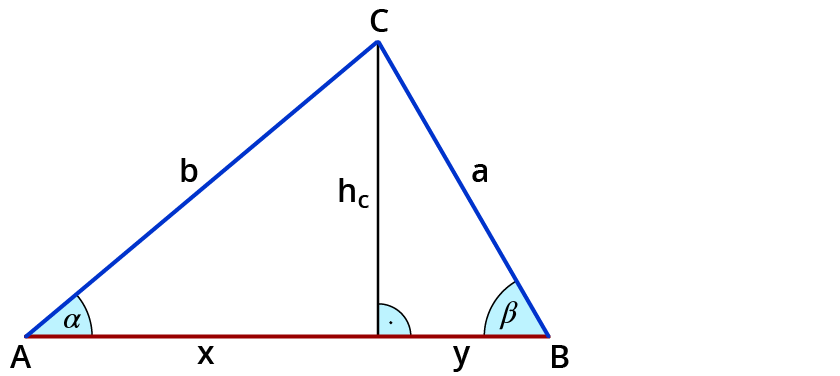
Seite $$y$$:
$$cos beta = y/a$$ $$|*a$$
$$a * cos beta = y$$
$$6 * cos 60^° = y$$
$$3$$ $$cm$$ $$=y$$
Höhe $$h_c$$:
$$sin beta = h_c / a$$ $$|*a$$
$$a * sin beta = h_c$$
$$6 * sin 60^° = h_c$$
$$5,20$$ $$cm$$ $$=h_c$$
Seite $$x$$:
$$tan alpha = h_c /x$$ $$|*x$$
$$x * tan alpha = h_c$$ $$|: tan alpha$$
$$x = h_c / tan alpha$$
$$x = 5,20/tan 40^°$$
$$x = 6,20$$ $$cm$$
Seite $$c$$:
$$c = x+y$$
$$c = 6,20 + 3$$
$$c = 9,20$$ $$cm$$
Fertig! Die Seite $$c$$ ist $$9,20$$ $$cm$$ lang.
Strategie:
Zerlegen in 2 rechtwinklige Dreiecke
Rechne mit gerundeten Zwischenergebnissen weiter.
Ergänzen
Du kannst ein Dreieck auch zu einem rechtwinkligen Dreieck ergänzen. Wenn du die Höhe einzeichnest, liegt sie außerhalb des Dreiecks.
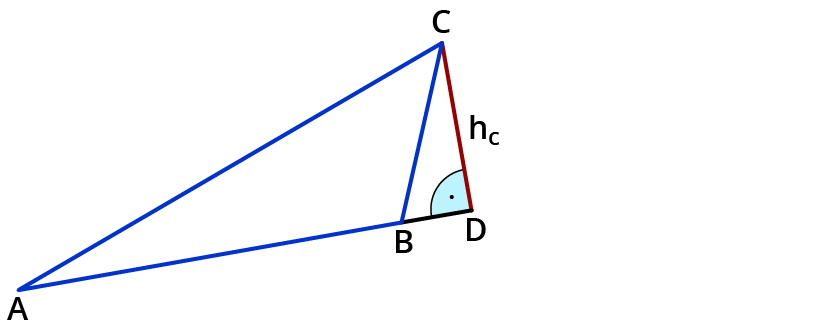
Stumpfwinklige Dreiecke kannst du zu einem rechtwinkligen Dreieck ergänzen oder zerlegen.
Stumpfer Winkel:
$$alpha$$ liegt zwischen $$90^°$$ und $$180^°$$. $$90^° < alpha <180^°$$

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beispielaufgabe Ergänzen
In diesem Dreieck beträgt der Winkel $$α = 20^°$$ und der Winkel $$β= 115^°$$. Die Höhe $$h_c$$ ist $$20$$ $$cm$$ lang.
Berechne die Seite $$b$$ und die Seite $$a$$.
Lösung:
Zeichne die Höhe ein und ergänze zum rechtwinkligen Dreieck.
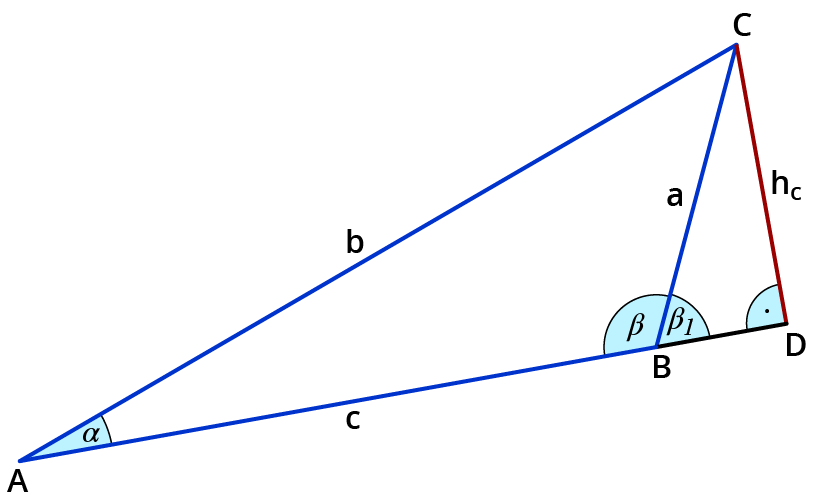
Seite $$b$$:
$$sin alpha= h_c / b$$ $$|*b$$
$$b * sin alpha = h_c$$ $$|:sin alpha$$
$$b = h_c/ sin alpha$$
$$b = 20/ sin 20^°$$
$$b = 58,48$$ $$cm$$
Seite $$a$$:
Zuerst berechnest du den Winkel $$beta_1$$:
$$beta_1 = 180^°-beta$$
$$beta_1=180^°-115^°$$
$$beta_1=65^°$$
Jetzt kannst du $$a$$ berechnen:
$$sin beta_1 = h_c / a$$ $$|*a$$
$$a * sin beta_1 = h_c$$ $$|: sin beta_1$$
$$a = h_c / sin beta_1$$
$$a = 20 / sin 65^°$$
$$a = 22,07$$ $$cm$$
Strategie:
Zerlegen in 2 rechtwinklige Dreiecke
$$beta$$ und $$beta_1$$ sind Nebenwinkel. Nebenwinkel sind zusammen $$180^°$$ groß.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen