Umkehrfunktionen untersuchen
Was ist eine Umkehrfunktion?
Ein Liter Kraftstoff der Marke Super-Extra-Mega-Power kostet 2 €.
Familie Sparsam berechnet die Kosten und erstellt eine Tabelle für die ZuordnungBenzin in $$l$$ $$rarr$$ Kosten in €:
| Benzin in $$l$$ | 0 | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|
| Kosten in € | 0 | 20 | 40 | 60 | 80 | 100 |
Zu dieser Zuordnung gehört die Funktionsgleichung y = f(x) = 2x.
Aus dieser Tabelle kannst du einer bestimmen Menge Benzin eindeutig die Kosten ablesen.
Umgekehrt geht’s auch: Du kannst einer Rechnung in € eindeutig die getankte Menge Benzin in $$l$$ zuordnen!
Eine Zuordnung mit dieser Eigenschaft wird als eindeutig umkehrbar bezeichnet.
Die entsprechende Funktion heißt dann Umkehrfunktion $$f^-1$$.
Die Funktionen $$f$$ und $$f^-1$$ heißen auch zueinander invers.
Die Graphen von $$f$$ und $$f^-1$$
Das Beispiel mit der Zuordnung Benzin in $$l$$ $$rarr$$ Kosten in €
führte auf die Funktionsgleichung y = f(x) = 2x und die Wertetabelle:
| Benzin in $$l$$ | 0 | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|
| Kosten in € | 0 | 20 | 40 | 60 | 80 | 100 |
Es handelt sich um eine lineare Funktion. Der Graph sieht so aus:

Aus der Wertetabelle und dem Graphen folgt, dass z.B. 20 l Benzin 40 € kosten.
Umgekehrt folgt eine Umrechnungstabelle von Kosten in € in Benzin in $$l$$ durch Vertauschen von Eingangs- und Ausgangsgröße der Zuordnung:
| Kosten in € | 0 | 20 | 40 | 60 | 80 | 100 |
|---|---|---|---|---|---|---|
| Benzin in $$l$$ | 0 | 10 | 20 | 30 | 40 | 50 |
Werden x- und y-Werte vertauscht, gehen die Punkte (10|20) bzw. (20|40) in die Punkte (20|10) bzw. (40|20) über.
Im Koordinatensystem ergibt das auch wieder eine Gerade. Sie geht durch Spiegelung des Graphen von f an der Winkelhalbierenden des 1. Quadranten hervor. Die Spiegelachse kannst du auch als Funktion angeben: f(x)=x.
Diese umgekehrte Zuordnung von $$f(x) = 2x$$ ist die Umkehrfunktion $$f^-1(x) = frac{1}{2}x$$.
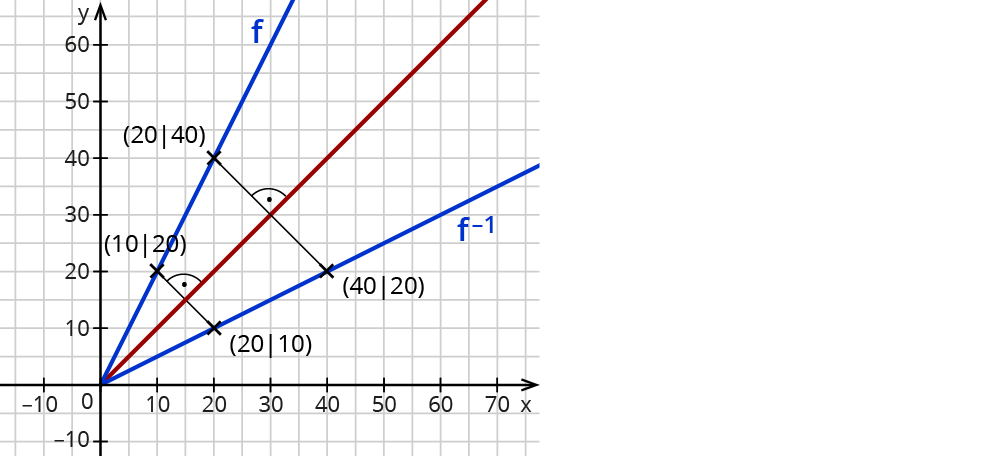
Den Graphen von $$f^(-1)$$ erhältst du, wenn du $$f$$ an dem Graphen von $$y=f(x)=x$$ spiegelst.
Gibt es zu jeder Funktion eine Umkehrfunktion?
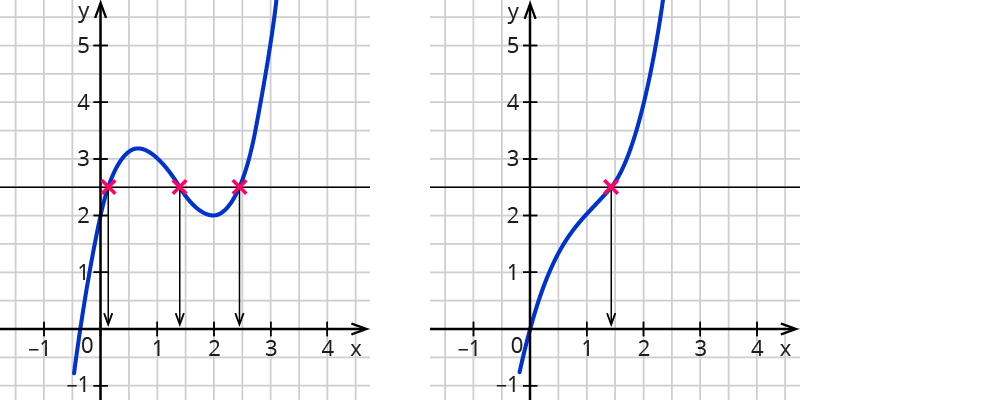
Linke Abbildung: Einer Zahl auf der y-Achse sind in diesem Beispiel drei Zahlen auf der x-Achse zugeordnet.
| x | 0 | 0,15 | 1 | 1,40 | 2 | 2,45 | 3 |
|---|---|---|---|---|---|---|---|
| y | 2 | 2,5 | 3 | 2,5 | 2 | 2,5 | 5 |
Diese Funktion ist nicht umkehrbar.
Rechte Abbildung: Jeder Zahl auf der y-Achse ist genau eine Zahl auf der x-Achse zugeordnet.
| x | 0 | 1 | 1,42 | 2 |
|---|---|---|---|---|
| y | 0 | 2 | 2,5 | 4 |
Diese Funktion ist umkehrbar.
Eine Funktion ist genau dann eindeutig umkehrbar, wenn jede Horizontale den Graphen einer Funktion nur in einem Punkt schneidet (Horizontalen-Test).

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Rechnerische Bestimmung von $$f^-1$$
Beispiel: $$y=f(x)=2x$$
1. Schritt: Auflösen von y = f(x) nach x:
$$2x = y = f(x) | : 2$$
$$ x = \frac{y}{2}$$
2. Schritt: Vertauschen der Variablen:
$$ y = \frac{x}{2}$$
3. Schritt: Notieren der Umkehrfunktion:
$$ f^-1(x) = \frac{x}{2}$$
Die hier angegebene Schrittfolge gilt allgemein für umkehrbare Funktionen.
Untersuchen von $$y = f(x) = 0,5x - 0,5$$
Bilden der Umkehrfunktion
1. Schritt: Auflösen von y = f(x) nach x:
$$0,5x-0,5 = y = f(x) | + 0,5$$
$$ 0,5x = y+0,5 | *2$$
$$ x = 2y+1$$
2. Schritt: Vertauschung der Variablen:
$$ y = 2x+1$$
3. Schritt: Notieren der Umkehrfunktion:
$$ f^-1(x) = 2x+1$$
Graphen von $$f(x)$$ und $$f^-1(x)$$
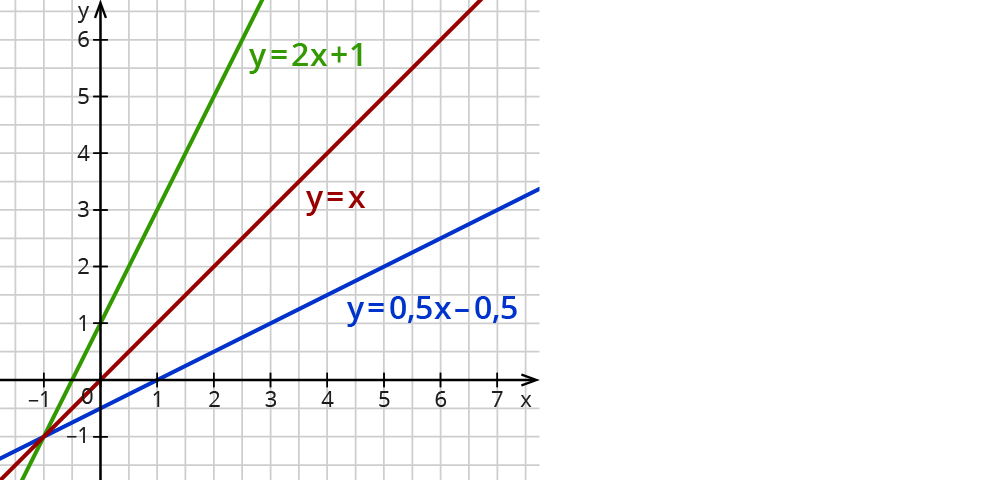
Untersuchen von $$y = f(x) = 0,5x - 0,5$$
Funktionswerte von $$f$$ und $$f^-1$$
Die Wertetabellen von $$f(x)=0,5x-0,5$$ und $$f^-1(x)=2x+1$$ lauten:
| x | $$f(x)$$ |
|---|---|
| x | $$f^-1(x)$$ |
|---|---|
Aus den Wertetabellen kannst du ablesen: für $$x = 5$$ folgt $$f(5) = 2$$.
Damit folgt: $$f^-1(2) = 5$$ sowie durch schrittweises Einsetzen:
$$f(f^-1(2)) = 2$$ und $$f^-1(f(5)) = 5$$.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Eigenschaften von Funktion $$f$$ und Umkehrfunktion $$f^-1$$
Eine Zuordnung, bei der jedem Wert x aus dem Definitionsbereich D genau ein Wert y aus dem Wertebereich W zugeordnet wird, ist eine Funktion.
Soll umgekehrt jedem y-Wert der zugehörige x-Wert zugeordnet werden, muss die Umkehrfunktion gebildet werden.
- Eine Funktion $$f$$, die eine Umkehrfunktion $$f^-1$$ besitzt, ist eine umkehrbare Funktion.
- Eine umkehrbare Funktion ist eine eindeutige Funktion.
- Die Funktionen $$f$$ und $$f^-1$$ werden auch als zueinander invers bezeichnet.
- Die Wertetabelle von $$f^-1$$ folgt aus der von $$f$$ durch Vertauschung von Eingangs- und Ausgangsgröße.
- Wenn für eine Funktion $$f$$ die Umkehrfunktion $$f^-1$$ existiert, gilt $$f(f^-1(x)) = f^-1(f(x)) = x$$.
- Der Graph von $$f^-1$$ folgt aus dem von $$f$$ durch Spiegelung an der Geraden y = x.
- Wird der Graph einer Funktion $$f$$ von jeder Horizontalen nur in einem Punkt geschnitten, so besitzt $$f$$ eine Umkehrfunktion $$f^-1$$.
- Die Funktionsgleichung von $$f^-1$$ folgt aus der von $$f$$ durch Vertauschung von x und y in f(x) und Auflösung der entstehenden Gleichung nach y.
| $$f$$ | $$f^-1$$ | |
|---|---|---|
| Funktionsgleichung | y = f(x) | x = $$f^-1$$(y) |
| Definitionsbereich D | x-Werte | y-Werte |
| Wertebereich W | y-Werte | x-Werte |
| Wertepaare | ( x | y ) | ( y | x ) |
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen