Kurven in Parameterdarstellung
Parameterdarstellung von Kurven
In Mathe hast du schon ganz viele Punkte in der Form P(x|y) aufgeschrieben. Mit den Koordinaten x und y gibst du an, wo sich ein Objekt in der Ebene (nicht im Raum) befindet.
Stell dir ein Schiff vor, das innerhalb bestimmter Zeiten seinen Ort verändert.
Mathematisch: Das Schiff ändert seine Koordinaten x und y in Abhängigkeit der Zeit t. x und y sind also Funktionen der Zeit:
x = x(t) und y = y(t).
Mit diesen Funktionen kannst du zu jedem Zeitpunkt die Lage des Schiffs berechnen.
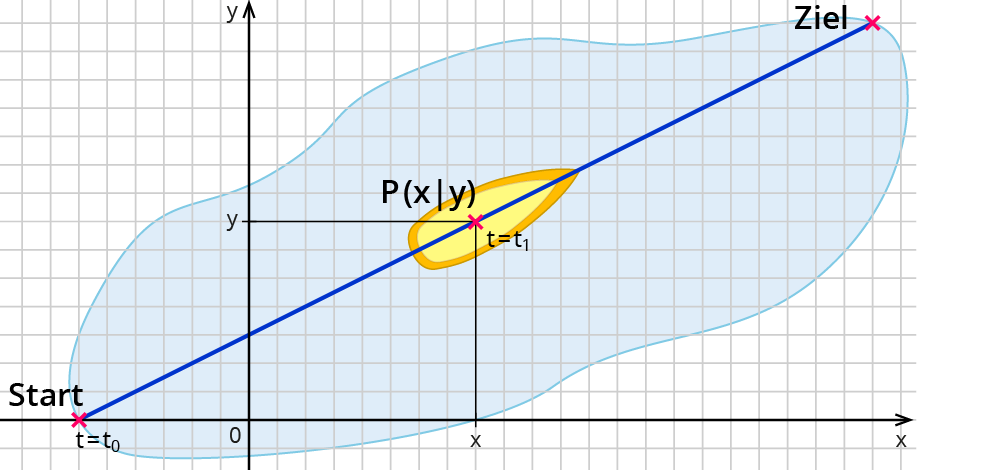
t0 und t1 sind Werte von t, z.B. 0 Stunden und 2 Stunden.
Solche Bewegungsvorgänge werden oft mit Parametergleichungen
x = x(t) und y = y(t) mit t als Parameter beschrieben.
Der Parameter t ist meistens eine reelle Zahl. Aber je nach Anwendung kann er eingeschränkt sein. Wenn t die Zeit ist, sind negative Zeiten (t<0) ja nicht sinnvoll.
Hier lernst du geradlinige und parabelförmige Bewegungen kennen.
Parameterdarstellung von Geraden
Beispiel 1
Gegeben sind folgende Parametergleichungen:
x(t) = t - 2 und y(t) = 2t - 3.
Daraus kannst du eine Wertetabelle erstellen:
| t | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| x(t) | -3 | -2 | -1 | 0 | 1 |
| y(t) | -5 | -3 | -1 | 1 | 3 |
Zeichne den Graphen:

Die Wertepaare (x|y) liegen auf einer Geraden mit der Steigung m = 2 und dem Achsenabschnitt n = 1. Die Geradengleichung lautet y = 2x + 1.
Die Geradengleichung kannst du auch aus den Parametergleichungen bestimmen.
- Löse x(t) nach t auf.
x(t) = t - 2 $$rArr$$ t = x + 2 - Setze in y(t) den Term für t ein.
t = x + 2 in y = 2t - 3 $$rArr$$ y = 2(x+ 2) - 3 - Vereinfache die Geradengleichung.
y = 2(x+ 2) - 3 = 2x + 1
Parameterform von Geraden
Beispiel 1
Gegeben sind folgende Parametergleichungen:
x(t) = -3t + 5 und y(t) = 4t + 3.
Erstelle eine Wertetabelle:
| t | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| x(t) | 5 | 2 | -1 | -4 |
| y(t) | 3 | 7 | 11 | 15 |
Zeichne den Graphen:

Bei dieser Geraden kannst du nicht mehr bequem die Geradengleichung ablesen.
- Löse x(t) nach t auf.
$$x(t) = -3 t +5$$ $$rArr$$ $$t=-x/3+5/3$$ - Setze in y(t) den Term für t ein.
$$t=-x/3+5/3$$ in $$y(t) = 4t + 3$$ $$rArr$$ $$y = 4(-x/3+5/3) + 3$$ - Vereinfache die Geradengleichung.
$$y = -4/3x+29/3$$
Die Wertepaare (x|y) liegen also auf einer Geraden mit der
Steigung $$m = - frac{4}{3}$$ und dem Achsenabschnitt $$n = frac{29}{3}$$.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Gerade und Kreis
Ein Objekt bewegt sich mit konstanter Geschwindigkeit so, dass ein Ort
(x|y) durch folgende Parametergleichungen beschrieben wird:
$$x(t) = t - 1$$ und $$y(t) = t + 1$$.
Zu welcher Zeit t und an welchen Orten (x|y) kreuzt das Objekt den Kreis, der durch die Gleichung $$(x - 1)^2 + (y - 2)^2 = 5$$ beschrieben wird?
Lösung:
Wertetabelle für die Parametergleichungen:
| t | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| x(t) | -1 | 0 | 1 | 2 |
| y(t) | 1 | 2 | 3 | 4 |
Wertetabelle für den Kreis mit dem Mittelpunkt bei (1|2):
| x | -1 | 0 | 2 | 3 |
|---|---|---|---|---|
| $$y_1$$ | 1 | 0 | 0 | 1 |
| $$y_2$$ | 3 | 4 | 4 | 3 |
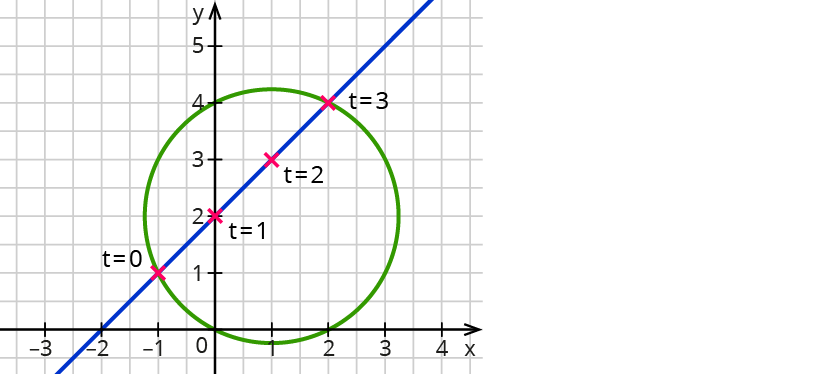
Zu den Zeiten $$t_1 = 0$$ und $$t_2 = 3$$ kreuzt das Objekt in den Punkten
(-1|1) und (2|4) den Kreis.
Viele dieser Aufgaben lassen sich leicht mit Programmen wie Geogebra oder einem grafikfähigen Taschenrechner (GTR) lösen.
Parameterform von Parabeln
Die Parameterform gibt es nicht nur für Geraden, sondern auch für Parabeln. Parabeln brauchst du für kompliziertere Bewegungen wie den waagerechten Wurf.
Die Bahnkurve für den waagerechten Wurf
Beim waagerechten Wurf wird ein Objekt mit einer bestimmten Geschwindigkeit horizontal in x-Richtung abgeworfen. Wegen der Erdanziehung überlagert sich die Bewegung mit dem freien Fall in y-Richtung nach unten. Physiker nennen das „Prinzip von der ungestörten Überlagerung von Bewegung“.
Beispiel:
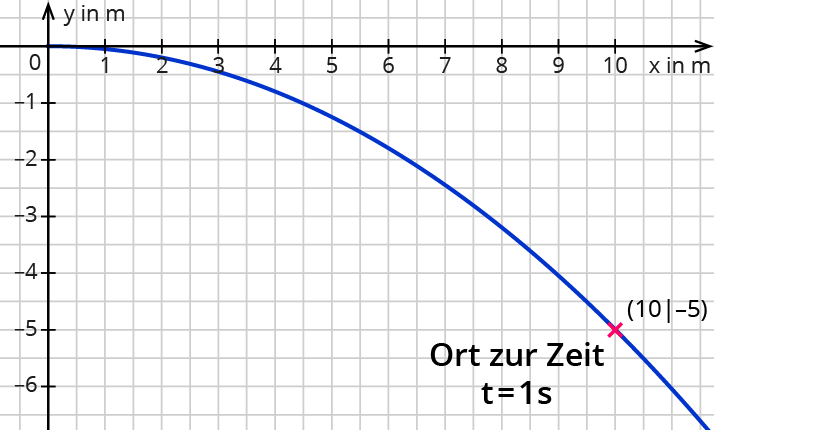
Ein Objekt wird waagerecht mit $$v = 10 m/s$$ geworfen. Für die Erdbeschleunigung $$g$$ gilt: $$g approx 10 m/s^2$$.
Daraus folgt:
- Parametergleichung für den Wurf in x-Richtung: $$x(t) = 10 t$$
- Parametergleichung für Erdanziehung in y-Richtung:
Aus der Physik ist das Zeit-Weg-Gesetz für den freien Fall bekannt: $$s(t) = -frac{g}{2}t^2$$ . Werden für $$g approx 10$$ sowie $$s$$ durch $$y$$ ersetzt, so folgt (wir notieren ohne Einheiten)
$$y(t) = -5 t^2$$ mit $$tge0$$.
Wenn du $$x(t)$$ nach $$t$$ umstellst und in $$y(t)$$ einsetzt, bekommst du als Bahnkurve eine Parabel. Das ist die Wurfparabel: $$y = -1/20 x^2$$.
Parameterform von Parabeln
Beispiel 2
Gegeben sind folgende Parametergleichungen:
$$x(t) = t + 1$$ und $$y(t) = t^2$$. Erstelle eine Wertetabelle:
| t | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| x(t) | -1 | 0 | 1 | 2 | 3 |
| y(t) | 4 | 1 | 0 | 1 | 4 |
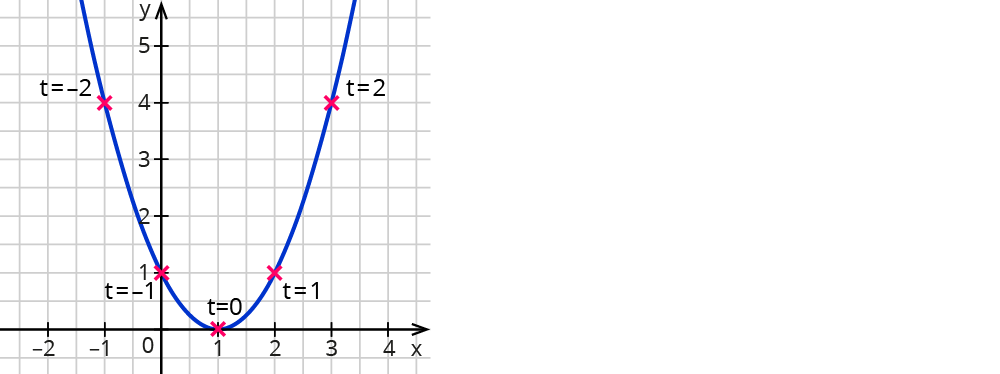
Die Wertepaare (x|y) liegen auf einer Parabel.
Bestimme die Parabelgleichung:
- Löse x(t) nach t auf.
x(t) = t + 1 $$rArr$$ t = x - 1 - Setze in y(t) den Term für t ein.
t = x - 1in y = t² $$rArr$$ y = (x - 1)² - Vereinfache die Parabelgleichung.
y = (x - 1)² = x² - 2x + 1

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen