Parameter quadratischer Funktionen untersuchen 2
Verschieben nach oben und unten
Beim Untersuchen von Parabeln gehst du immer von der Normalparabel mit den bekannten Punkten $$(0|0), (1|1), (-1|1), (2|4), (-2|4)$$ aus.

Der Einfluss des Parameters $$e$$ bei $$f(x)=x^2+e$$:
Du kannst die Normalparabel entlang der $$y$$-Achse nach oben und unten verschieben.
Das bewirkt der Parameter $$e$$ in $$f(x)=x^2+e$$.
$$f(x)=x^2=x^2+0$$
Bei der Funktionsgleichung der Normalparabel ist der Wert des Parameters $$e$$ gleich Null.
Der Einfluss des Parameters $$e$$ für $$e=+2$$
Für $$e=+2$$ lautet die Gleichung der quadratischen Funktion $$f(x)=x^2+$$$$(+2)$$$$=x^2+2$$
Mit der Wertetabelle kannst du den Einfluss des Parameters im Vergleich zur Normalparabel sehen.
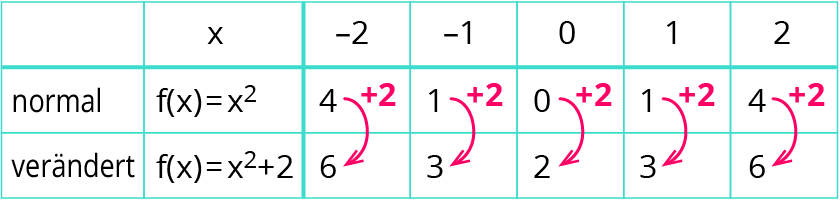
Rechenbeispiel: $$f(1)=1^2+2=1+2=3$$
Die $$y$$-Werte der Punkte der Normalparabel werden alle um den Wert $$2$$ erhöht. Die Normalparabel ist um zwei Einheiten nach oben verschoben.
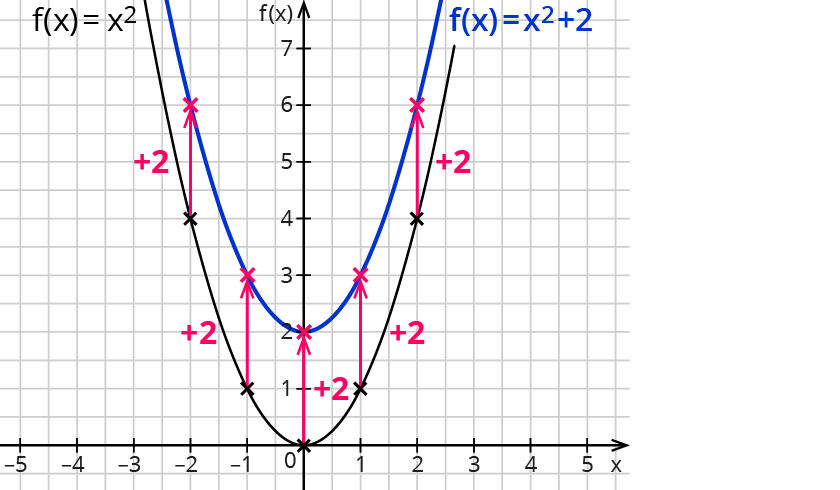
Du siehst, dass die roten Verschiebungspfeile parallel zur $$y$$-Achse verlaufen. Deshalb sprechen Mathematiker von der „Verschiebung parallel zur $$y$$-Achse“.
Der Scheitelpunkt der Parabel hat sich von $$(0|0)$$ zu $$(0|2)$$ geändert.
Er wurde um zwei Einheiten nach oben verschoben.
Der Einfluss des Parameters $$e$$ für $$e=-3$$
Für $$e=-3$$ heißt die Gleichung der quadratischen Funktion $$f(x)=x^2+$$$$(-3)$$$$=x^2-3$$
Die Wertetabelle dazu:
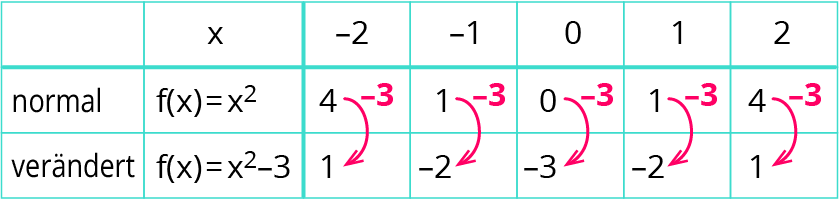
Rechenbeispiel: $$f(-1)=(-1)^2-3=1-3=-2$$
Die $$y$$-Werte der Punkte der Normalparabel werden alle um den Wert $$3$$ vermindert. Die Normalparabel verschiebt sich um drei Einheiten nach unten.
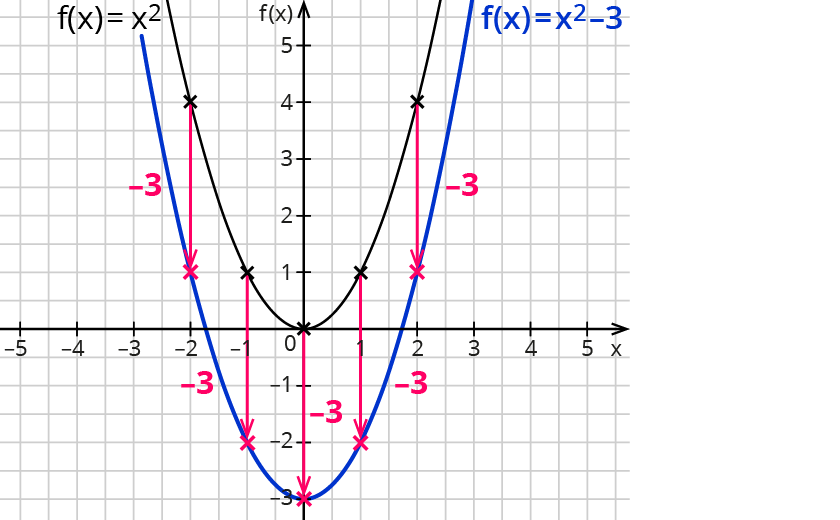
Der Scheitelpunkt der Parabel hat sich von $$(0|0)$$ zu $$(0|-3)$$ geändert.
Er wurde um drei Einheiten nach unten verschoben.
Im Überblick
Der Parameter $$e$$ bei $$f(x)=x^2+e$$ bewirkt:
- Ist $$e$$ positiv, so wird die Normalparabel um $$e$$ Einheiten nach oben verschoben.
- Ist $$e$$ negativ, so wird die Normalparabel um $$e$$ Einheiten nach unten verschoben.
Der Scheitelpunkt liegt bei $$S(0|e)$$.
Probiere es hier einmal selber aus: verändere e und beobachte, was passiert.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen