Strecken und Stauchen der Normalparabel

Den Verlauf des Graphen der Normalparabel kennst du schon:

Am besten ist, du hast die wichtigsten Punkte des Graphen im Kopf: $$(0|0) , (1|1) , (-1|1) , (2|4) , (-2|4)$$.

Der Parameter $$a$$ in $$f(x)=a*x^2$$

Manchmal brauchst du aber auseinandergebogene oder zusammengebogene Parabeln. Dann brauchst du den Parameter $$a$$ in der Funktionsgleichung.

In der Sprache der Mathematik heißt es:

• Auseinanderbiegen = Stauchen
  
• Zusammenbiegen = Strecken

Was bewirkt der Parameter $$a$$ für $$a=2$$?

Für $$a=2$$ heißt die Funktionsgleichung der quadratischen Funktion $$f(x)=$$$$2$$$$*x^2$$.

Mit einer Wertetabelle siehst du, wie sich der Graph von $$f(x)=$$$$2$$$$*x^2$$ im Vergleich zur Normalparabel ändert.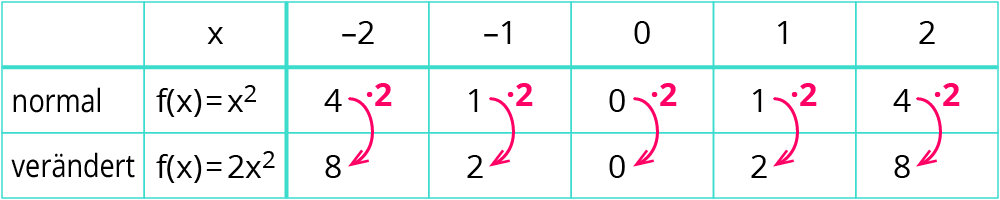

Rechenbeispiel: $$f(-1)=2*(-1)^2=2*1=2$$

Der Faktor $$2$$ bewirkt, dass die $$y$$-Werte der Punkte der Normalparabel verdoppelt werden. Der Graph sieht so aus: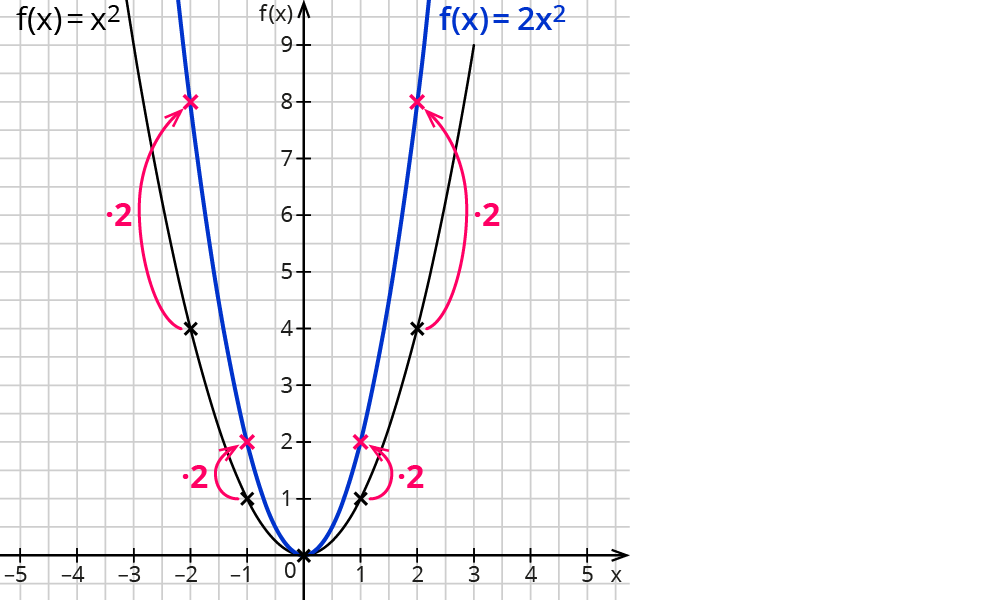

Der „veränderte“ Graph ist im Vergleich zur Normalparabel zusammen gebogen.
Zum $$x$$-Wert 1 gehört jetzt der $$y$$-Wert 2. Deshalb steigt der neue Graph schneller an.
Mathematisch heißt es: Die neue Parabel ist eine Streckung der Normalparabel um den Faktor „2“.

Was bewirkt der Parameter $$a$$ für $$a=1/2$$?

Für $$a=1/2$$ heißt die Funktionsgleichung der quadratischen Funktion $$f(x)=$$$$1/2$$$$x^2$$.
Hier sieht die Wertetabelle wir folgt aus:

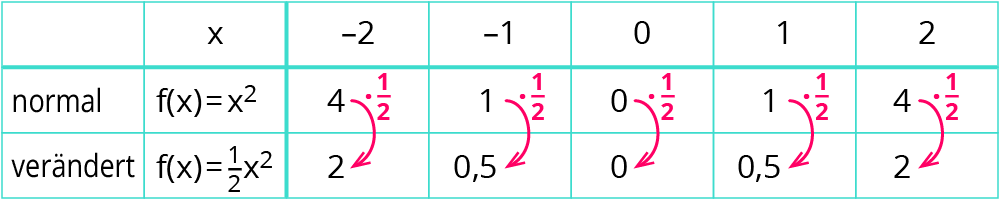
Rechenbeispiel: $$f(-2)=1/2*(-2)^2=1/2*4=2$$

Man kann erkennen, dass der Faktor $$1/2$$ die $$y$$-Werte der Punkte der Normalparabel halbiert. Der veränderte Graph sieht dann wie folgt aus:

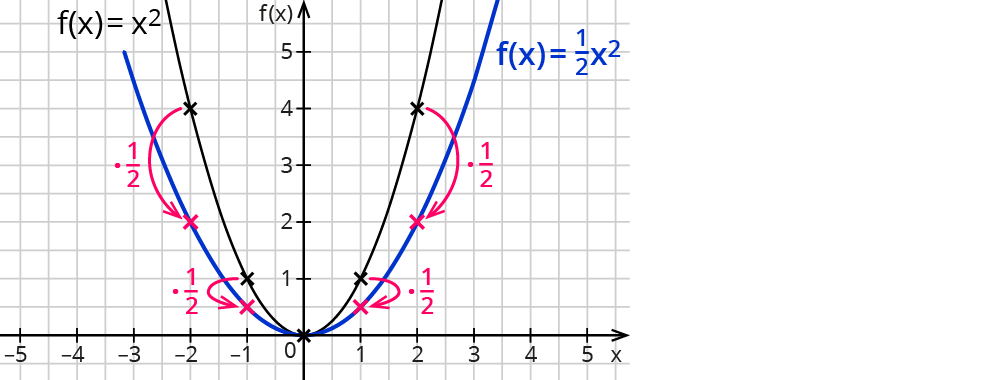
Der „veränderte“ Graph ist im Vergleich zur Normalparabel breiter geworden. Da z.B. zum $$x$$-Wert 2 jetzt der $$y$$-Wert 2 gehört (normal der $$y$$-Wert 4), steigt der neue Graph langsamer an.
Mathematisch sprechen wir von einer Stauchung der Normalparabel mit dem Faktor $$1/2$$.

Negativer Parameter $$a$$ mit $$a=-1$$

Was passiert eigentlich, wenn der Parameter $$a$$ negativ ist?
Für $$a=-1$$ heißt die Funktionsgleichung der quadratischen Funktion $$f(x)=$$$$-1$$$$*x^2=-x^2$$.

Zunächst wieder die Wertetabelle:

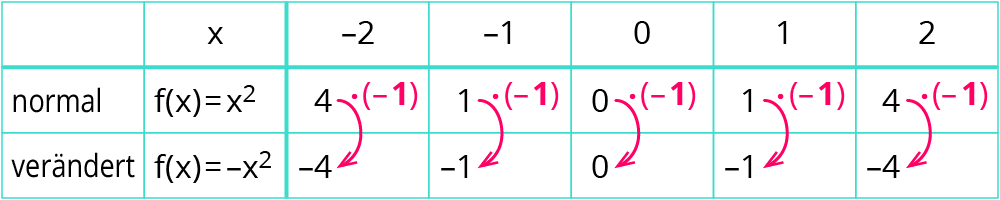
Rechenbeispiel: $$f(-2)=(-1)*(-2)^2=(-1)*4=-4$$

Der Faktor $$-1$$ bewirkt, dass die „normalen“ $$y$$-Werte negativ werden. Der veränderte Graph sieht dann wie folgt aus:

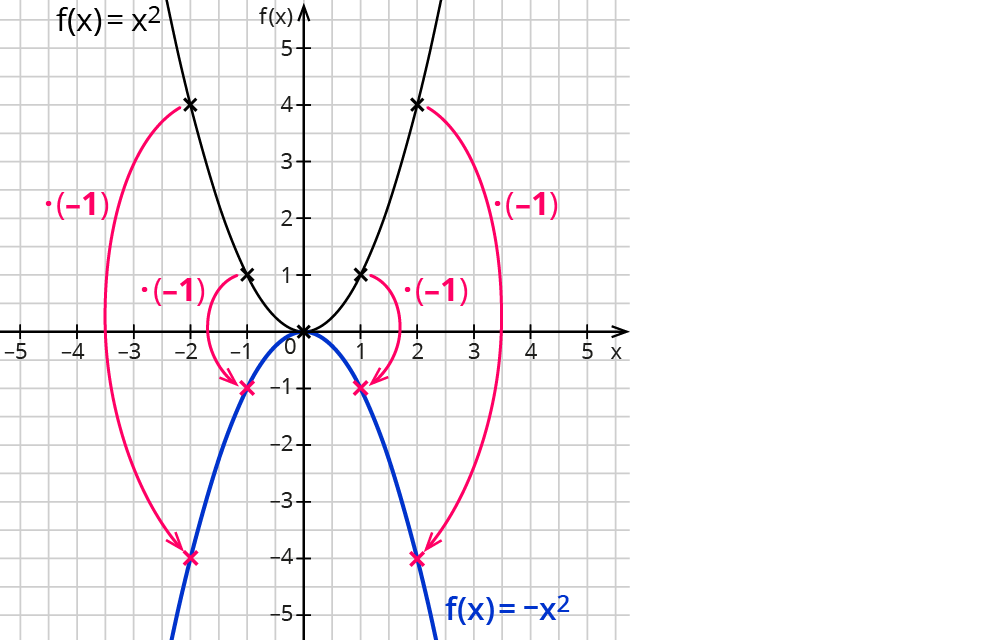
Der „veränderte“ Graph ist im Vergleich zur Normalparabel weder breiter noch schmaler geworden. Er ist nach unten geöffnet. Der Graph von $$f(x)=-x^2$$ entsteht durch die Spiegelung der Normalparabel an der $$x$$-Achse.

Noch 2 Beispiele

Schau dir die zwei Beispiele für $$a=-2$$ und $$a=-1/2$$ an. Die Funktionen heißen $$f(x)=-2*x^2$$ und $$g(x)=-1/2*x^2$$.
Die beiden Wertetabellen:

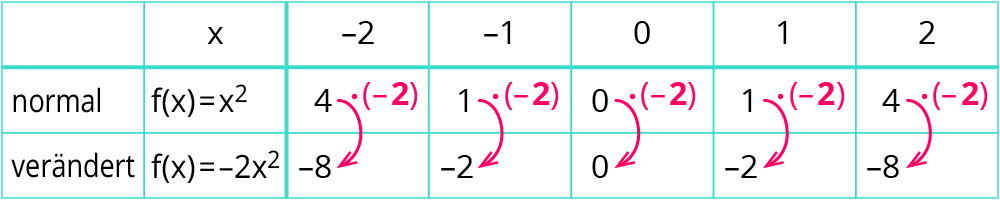
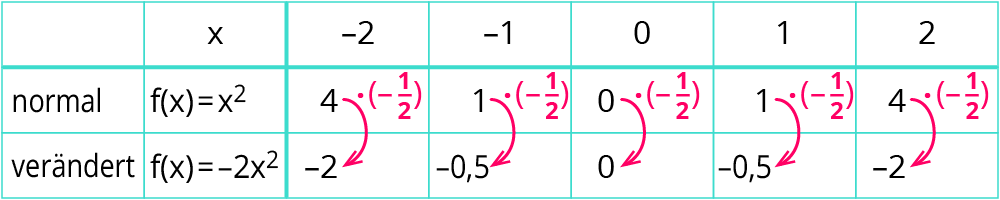
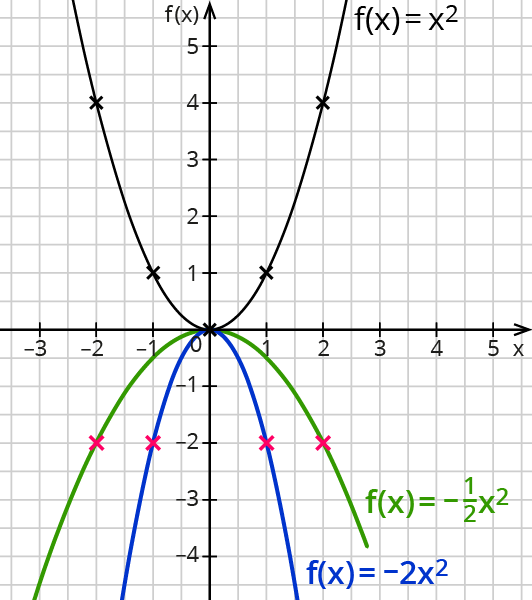
Die Graphen:

So kannst du die beiden Graphen beschreiben:

$$f(x)=-2*x^2$$

• Der Graph ist nach unten geöffent, weil der Parameter negativ ist.
• Der Graph ist gestreckt.

$$f(x)=-1/2*x^2$$

• Der Graph ist nach unten geöffnet, weil der Parameter negativ ist.
• Der Graph ist gestaucht.

Hier kannst du es auch ganz einfach selbst ausprobieren: verändere a und beobachte, was passiert.

Im Überblick

Der Parameter $$a$$ bei $$f(x)=a*x^2$$ bewirkt:

• Ist der Parameter $$a=1$$, so ist der Graph der Funktion die Normalparabel.
• Ist der Parameter $$a$$ größer als $$1$$ $$(a>1)$$ oder kleiner als $$-1$$ $$(a<-1)$$, so wird der Graph gegenüber der Normalparabel gestreckt.
• Hat der Parameter $$a$$ einen Wert zwischen $$-1$$ und $$1$$ $$(-1<a<1$$, außer $$0)$$, so wird der Graph gegenüber der Normalparabel gestaucht.
• Ist der Parameter $$a$$ negativ, so ist die Parabel nach unten geöffnet.
• Der Parameter $$a$$ darf nicht $$0$$ sein. Sonst wäre $$f(x)=0*x^2=0$$.
  
  

Veranschaulichen von „Strecken“ und „Stauchen“

Das Strecken der Normalparabel kannst du dir als als Zusammenbiegen oder Zusammendrücken der Normalparabel vorstellen.

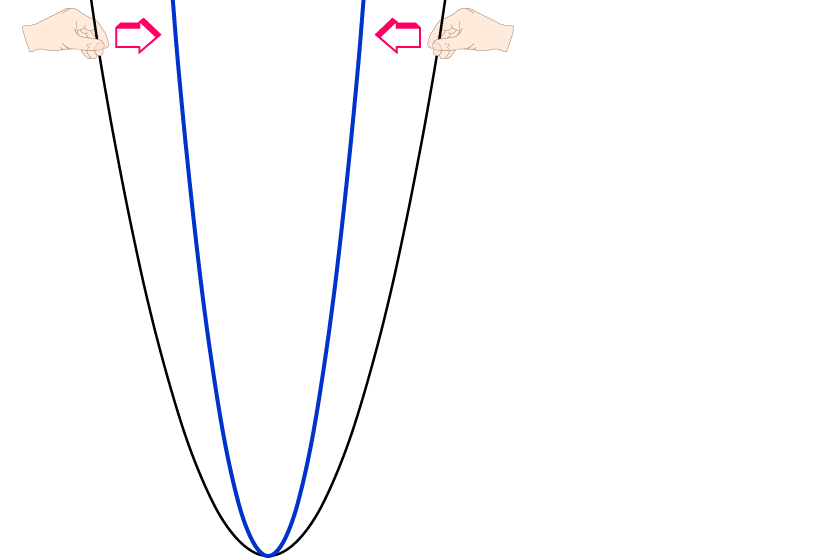
Das Stauchen der Normalparabel kannst du dir als Auseinanderbiegen oder Auseinanderziehen vorstellen.

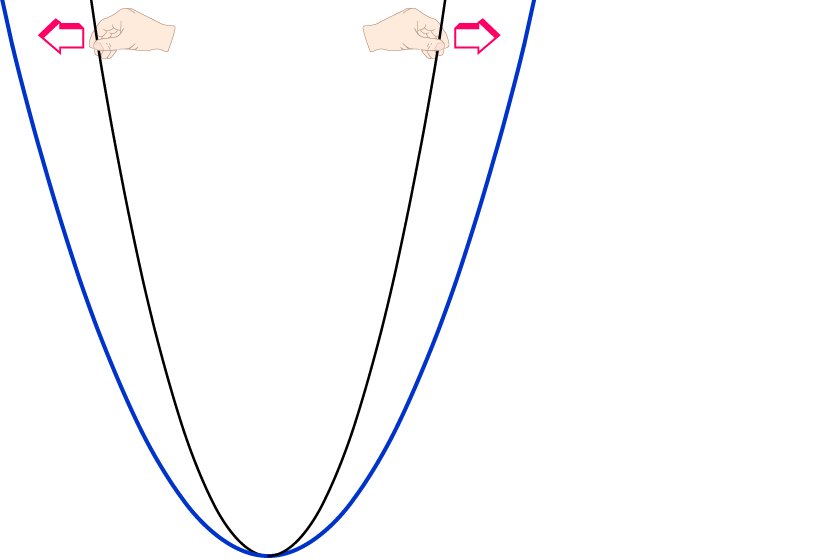
Für „faule“ Mathematiker: Die Betragsschreibweise

Du kannst sowas wie $$-1<a<1$$ für das Stauchen der Parabel noch kürzer aufschreiben.
Dazu nimmst du den Betrag: $$|a|<1$$
Gesprochen: Betrag von $$a$$ ist kleiner als $$1$$.

$$|a|<1$$ beinhaltet dieselben Zahlen wie $$-1<a<1$$

Warum?

Zwei Zahlen für $$a$$ aus $$-1<a<1$$ sind $$0,5$$ und $$-0,5$$. Es gilt: $$|-0,5|=|+0,5|=0,5$$.

Die Zahl $$+0,5$$ ist genauso weit entfernt von der Null wie $$-0,5$$. Es liegen also sowohl $$-0,5$$ und $$0,5$$ in $$|a|<1$$.