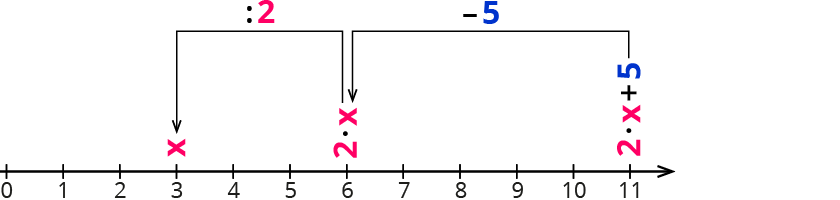
Gleichungen aufstellen
Zahlenrätsel 1
Aufgabe: Das Fünffache einer Zahl vermindert um $$6$$ entspricht dem Doppelten der Zahl vermehrt um $$9$$. Berechne die Zahl.
(1) Bestimme, wofür die Variable steht.
In der Aufgabenstellung findest du einen Hinweis, wie du die Variable festlegen musst.
Hier lautet die Aufgabenstellung: Berechne die Zahl.
$$x:$$ die gesuchte Zahl
(2) Übersetze den Text in die Sprache der Mathematik.
- das Fünffache einer Zahl: $$5x$$
- vermindert um $$6$$: $$-6$$
- entspricht: $$=$$
- das Doppelte einer Zahl: $$2x$$
- vermehrt um $$9$$: $$+9$$
(3) Stelle die Gleichung auf.
Die Gleichung lautet: $$5x-6=2x+9$$
Nun musst du die Gleichung lösen.
Antwort: Die gesuchte Zahl ist $$5$$.
(1) Bestimme als Erstes, wofür die Variable steht.
(2) Übersetze den Text in die Sprache der Mathematik.
(3) Stelle die Gleichung auf.
Meist wird die Variable mit $$x$$ bezeichnet.
Zahlenrätsel 2
Aufgabe: Die Summe dreier aufeinander folgender Zahlen ist gleich dem Vierfachen der größten der drei Zahlen vermindert um $$11$$. Bestimme die gesuchten drei Zahlen.
(1) Bestimme, wofür die Variable steht.
In der Aufgabenstellung findest du einen Hinweis, wie du die Variable festlegen musst.
Hier lautet die Aufgabenstellung: Bestimme die gesuchten drei Zahlen.
Die Variable $$x$$ kann sich aber nur auf eine Zahl beziehen. Wähle geschickt.
$$x:$$ die kleinste der gesuchten Zahlen
(2) Übersetze den Text in die Sprache der Mathematik.
- die auf $$x$$ folgende Zahl: $$x+1$$
- die auf $$x+1$$ folgende Zahl: $$x+2$$
- Summe: Addition ($$+$$)
- das Vierfache der größten Zahl: $$4(x+2)$$
- vermindert um $$11$$: $$-11$$
(3) Stelle die Gleichung auf.
Die Gleichung lautet: $$x+(x+1)+(x+2)=4(x+2)-11$$
Nun musst du die Gleichung lösen.
Antwort: Die gesuchten Zahlen sind $$6,7,8$$.
(1) Bestimme als Erstes, wofür die Variable steht.
(2) Übersetze den Text in die Sprache der Mathematik.
(3) Stelle die Gleichung auf.
Meist wird die Variable mit $$x$$ bezeichnet.
Altersrätsel
Aufgabe: Peter ist dreimal so alt wie Beate. In vier Jahren sind sie zusammen $$16$$ Jahre alt. Wie alt sind Beate und Peter heute?
(1) Bestimme, wofür die Variable steht.
In der Fragestellung findest du einen Hinweis, wie du die Variable festlegen musst.
Hier lautet die Fragestellung: Wie alt sind Beate und Peter heute?
Die Variable $$x$$ kann sich aber nur entweder auf das Alter von Beate oder das von Peter beziehen. Wähle geschickt.
$$x:$$ das Alter von Beate
(2) Übersetze den Text in die Sprache der Mathematik.
- Peter ist heute dreimal so alt wie Beate: $$3x$$
- Beates Alter in $$4$$ Jahren: $$x+4$$
- Peters Alter in $$4$$ Jahren: $$3x+4$$
- zusammen: Addition ($$+$$)
(3) Stelle die Gleichung auf.
Die Gleichung lautet: $$(x+4)+(3x+4)=16$$
Nun musst du die Gleichung lösen.
Antwort: Beate ist heute zwei Jahre und Peter sechs Jahre alt.
(1) Bestimme als Erstes, wofür die Variable steht.
(2) Übersetze den Text in die Sprache der Mathematik.
(3) Stelle die Gleichung auf.
Meist wird die Variable mit $$x$$ bezeichnet.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Geometrie
Aufgabe: Die Länge eines Rechtecks entspricht der dreifachen Breite vermindert um fünf Zentimeter. Der Umfang des Rechtecks beträgt $$22$$ $$cm$$. Berechne Länge und Breite des Rechtecks.
(1) Bestimme, wofür die Variable steht.
In der Aufgabenstellung findest du einen Hinweis, wie du die Variable festlegen musst.
Hier lautet die Aufgabenstellung: Berechne Länge und Breite des Rechtecks.
Die Variable $$x$$ kann sich aber nur entweder auf die Länge oder die Breite beziehen. Wähle geschickt.
$$x:$$ Breite des Rechtecks
(2) Übersetze den Text in die Sprache der Mathematik.
- Dreifache Breite: $$3x$$
- vermindert um $$5$$ $$cm$$: $$-5$$
- Länge des Rechtecks: $$3x-5$$
- Umfang des Rechtecks: Länge $$+$$ Breite $$+$$ Länge $$+$$ Breite
(3) Stelle die Gleichung auf.
Die Gleichung lautet: $$(3x-5)+x+(3x-5)+x=22$$
Nun musst du die Gleichung lösen.
Antwort: Die Breite des Rechtecks beträgt $$4$$ cm und die Länge $$7$$ cm.
(1) Bestimme als Erstes, wofür die Variable steht.
(2) Übersetze den Text in die Sprache der Mathematik.
(3) Stelle die Gleichung auf.
Meist wird die Variable mit $$x$$ bezeichnet.
Alltag 1
Aufgabe: Eine Kerze von $$20$$ cm Größe brennt jede Stunde um $$15$$ mm ab. Eine andere Kerze ist $$25$$ cm groß, brennt aber jede Stunde um $$20$$ mm ab. Nach wie vielen Stunden sind die Kerzen gleich groß?
(1) Bestimme, wofür die Variable steht.
In der Aufgabenstellung findest du einen Hinweis, wie du die Variable festlegen musst.
Hier lautet die Fragestellung: Nach wie vielen Stunden sind die Kerzen gleich groß?
Du musst hier auf die unterschiedlichen Einheiten achten.
$$x:$$ Brenndauer der Kerzen
(2) Übersetze den Text in die Sprache der Mathematik.
- Abbrennen von $$15$$ mm ($$1,5$$ cm) pro Stunde: $$-1,5x$$
- Erste Kerze nach $$x$$ Stunden: $$20-1,5x$$
- Abbrennen von $$20$$ mm ($$2$$ cm) pro Stunde: $$-2x$$
- Zweite Kerze nach $$x$$ Stunden: $$25-2x$$
(3) Stelle die Gleichung auf.
Die Gleichung lautet: $$20-1,5x=25-2x$$
Nun musst du die Gleichung lösen.
Antwort: Nach 10 Stunden sind die Kerzen gleich groß.
(1) Bestimme als Erstes, wofür die Variable steht.
(2) Übersetze den Text in die Sprache der Mathematik.
(3) Stelle die Gleichung auf.
Meist wird die Variable mit $$x$$ bezeichnet.
Alltag 2
Aufgabe: Du hast $$39$$ € Taschengeld gespart und gibst heute alles für insgesamt acht Comic-Hefte und CDs aus. Wie viele Comic-Hefte und wie viele CDs hast du gekauft, wenn jedes Comic-Heft $$4,50$$ € und jede CD $$5,50$$ € gekostet hat?
(1) Bestimme, wofür die Variable steht.
In der Fragestellung oder Aufgabenstellung findest du einen Hinweis, wie du die Variable festlegen musst.
Hier lautet die Fragestellung: Wie viele Comic-Hefte und wie viele CDs hast du gekauft?
Die Variable $$x$$ kann sich aber nur entweder auf die Anzahl der Comic-Hefte oder die Anzahl der CDsbeziehen.
$$x:$$ Anzahl der CDs
(2) Übersetze den Text in die Sprache der Mathematik.
- Anzahl der Comic-Hefte: $$8-x$$
- in CDs investiertes Geld: $$5,50x$$
- in Comic-Hefte investiertes Geld: $$4,50(8-x)$$
(3) Stelle die Gleichung auf.
Die Gleichung lautet: $$5,50x+4,50(8-x)=39$$
Nun musst du die Gleichung lösen.
Antwort: Du hast fünf Comic-Hefte und drei CDs gekauft.
(1) Bestimme als Erstes, wofür die Variable steht.
(2) Übersetze den Text in die Sprache der Mathematik.
(3) Stelle die Gleichung auf.
Meist wird die Variable mit $$x$$ bezeichnet.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen