Was ist eine Winkelhalbierende?

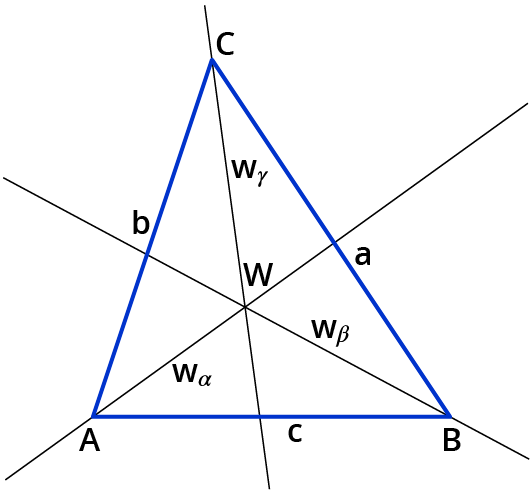
Die Winkelhalbierenden eines Dreiecks

• teilen die Winkel der Eckpunkte in zwei gleich große Teilwinkel.
• schneiden sich in einem Punkt `W`.

Der Punkt `W` ist der Mittelpunkt des Inkreises eines Dreiecks.

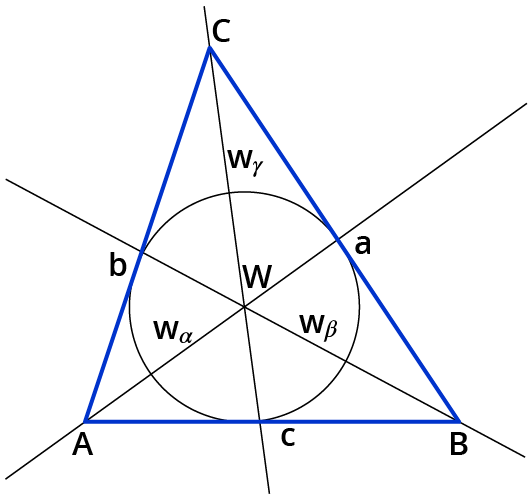
Was ist der Inkreis eines Dreiecks?

Der Inkreis eines Dreiecks berührt alle drei Seiten des Dreiecks. Das heißt, der Mittelpunkt ist von allen drei Seiten gleich weit entfernt.

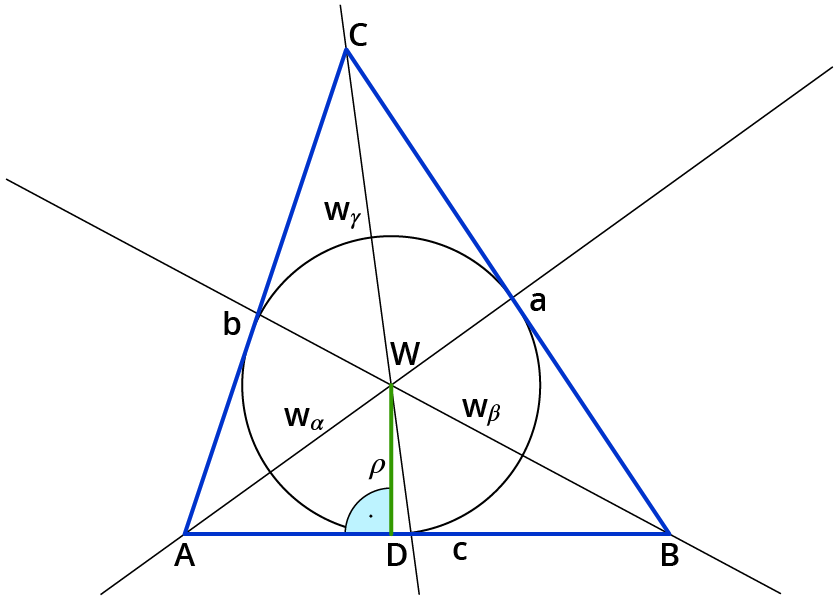
Wozu ist der Inkreis nützlich?

Lisas Mutter hat in der Wohnung einen neuen Bodenbelag aus Kork ausgelegt. Dabei sind dreieckige Reste übrig geblieben.
Lisa möchte die Reste nutzen, um unterschiedlich große kreisförmige Untersetzer für Tassen oder Töpfe herzustellen. Die Untersetzer sollen möglichst groß sein, damit nicht zu viel Material weggeworfen wird.

Für solche Aufgaben konstruierst du die Winkelhalbierenden und dann den Inkreis. Auf den folgenden Seiten siehst du, wie es geht.

So konstruierst du die erste Winkelhalbierende `w_alpha`

1. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt `A` ein.

Zeichne einen Kreisbogen um den Eckpunkt `A`, sodass er die Seiten `b` und `c` schneidet.

Du erhältst zwei Schnittpunkte `A_1` und `A_2`.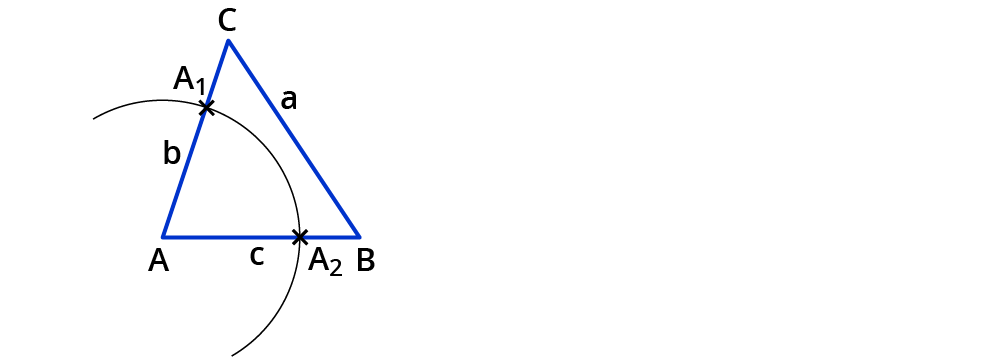

2. Schritt:
Stich mit der Zirkelspitze in `A_1` ein.

Wähle eine Zirkelspanne, die größer ist als die Hälfte der Strecke `bar(A_1A_2)`. Zeichne damit einen Kreisbogen um `A_1`.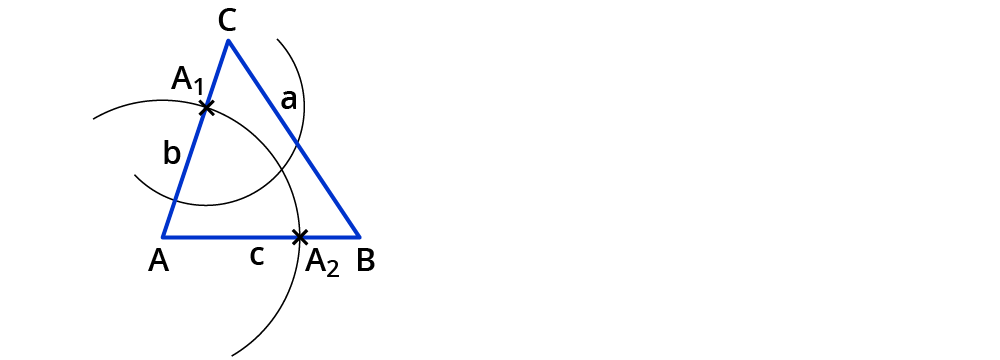



Zeichne mit derselben Zirkelspanne einen Kreisbogen um `A_2`.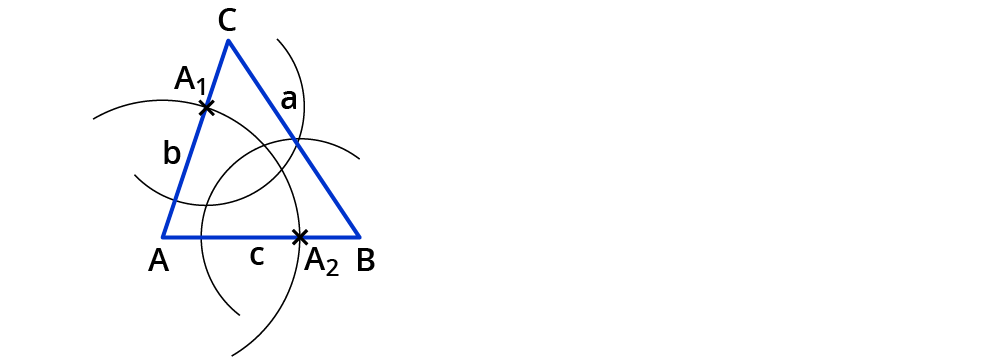

Du erhältst zwei Schnittpunkte der Kreisbögen.

Hier kannst du die Schritte noch einmal interaktiv ausführen:

Fast fertig mit `w_alpha`

3. Schritt:
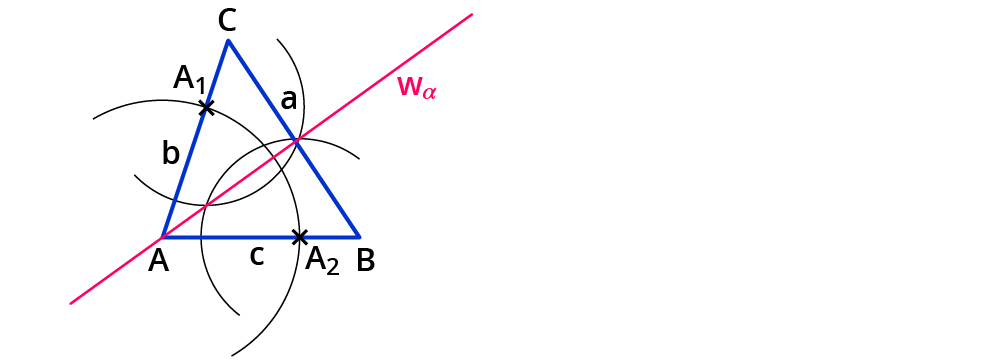
Verbinde den Schnittpunkt mit dem Eckpunkt `A` mithilfe eines Lineals.

Du hast die Winkelhalbierende des Winkels `alpha` konstruiert. Bezeichne sie mit `w_alpha`.

So konstruierst du die zweite Winkelhalbierende `w_beta`

1. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt `B` ein.

Zeichne einen Kreisbogen um den Eckpunkt `B`, sodass er die Seiten `a` und `c` schneidet.

Du erhältst zwei Schnittpunkte `B_1` und `B_2`.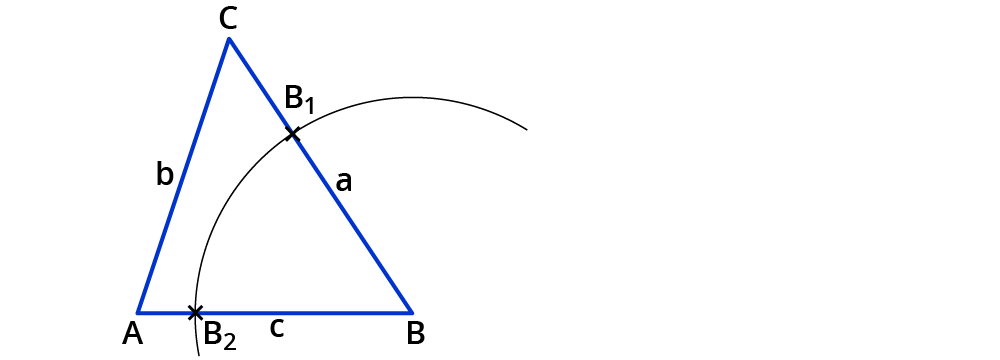



2. Schritt:
Stich mit der Zirkelspitze in `B_2` ein.

Wähle eine Zirkelspanne, die größer ist als die Hälfte der Strecke `bar(B_1B_2)`. Zeichne damit einen Kreisbogen um `B_2`.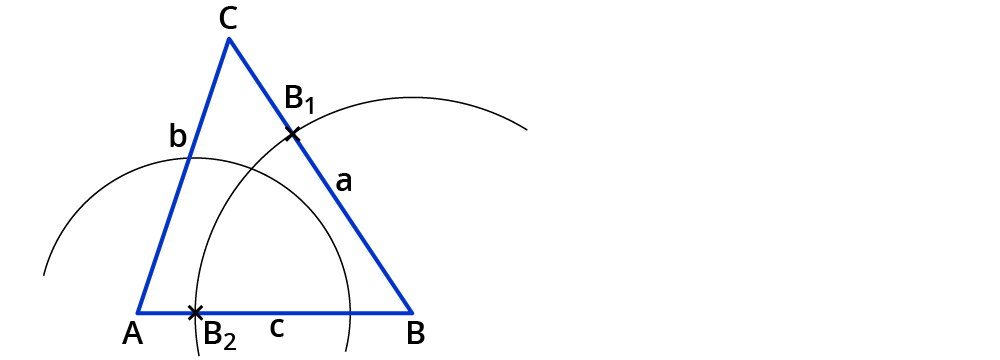



Zeichne mit derselben Zirkelspanne einen Kreisbogen um `B_1`.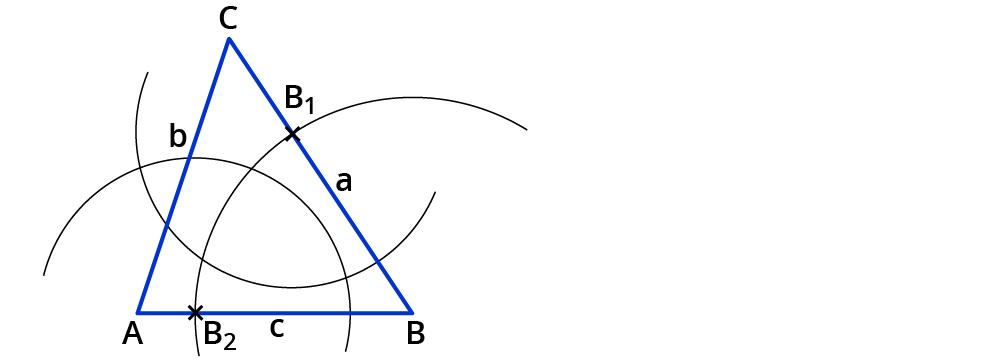



Du erhältst einen Schnittpunkt der Kreisbögen.

Fast fertig mit `w_beta`

3. Schritt:
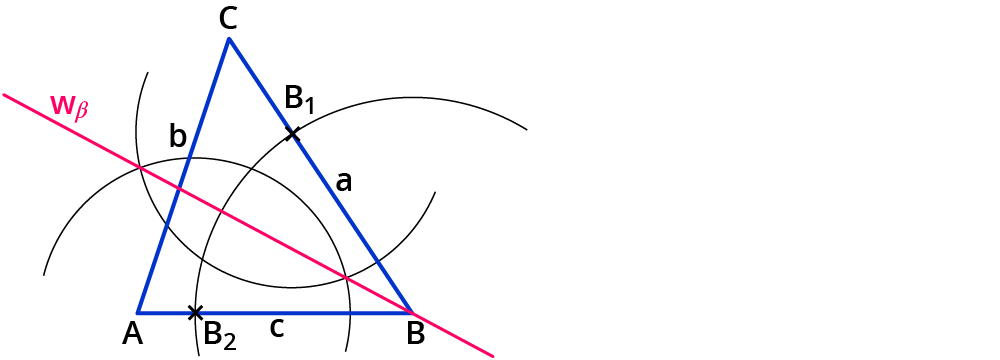
Verbinde den Schnittpunkt mit dem Eckpunkt `B` mithilfe eines Lineals.

Du hast die Winkelhalbierende des Winkels `beta` konstruiert.
Bezeichne sie mit `w_beta`.

So konstruierst du die letzte Winkelhalbierende `w_gamma`

1. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt `C` ein.

Zeichne einen Kreisbogen um den Eckpunkt `C`, sodass er die Seiten `a` und `b` schneidet.

Du erhältst zwei Schnittpunkte `C_1` und `C_2`.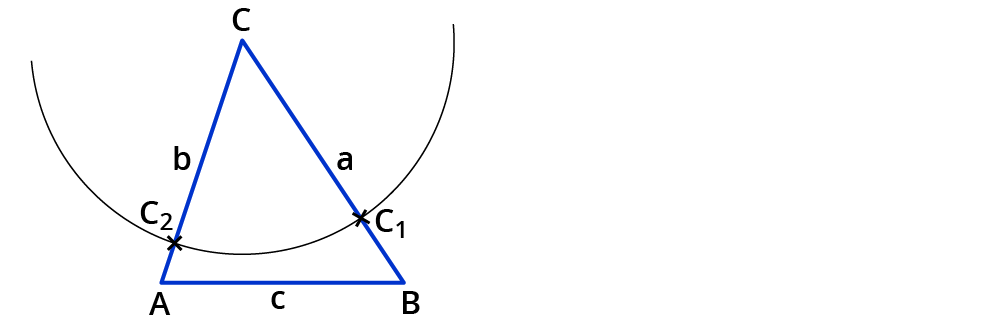

2. Schritt:
Stich mit der Zirkelspitze in `C_2` ein.

Wähle eine Zirkelspanne, die größer ist als die Hälfte der Strecke `bar(C_1C_2)`. Zeichne damit einen Kreisbogen um `C_2`.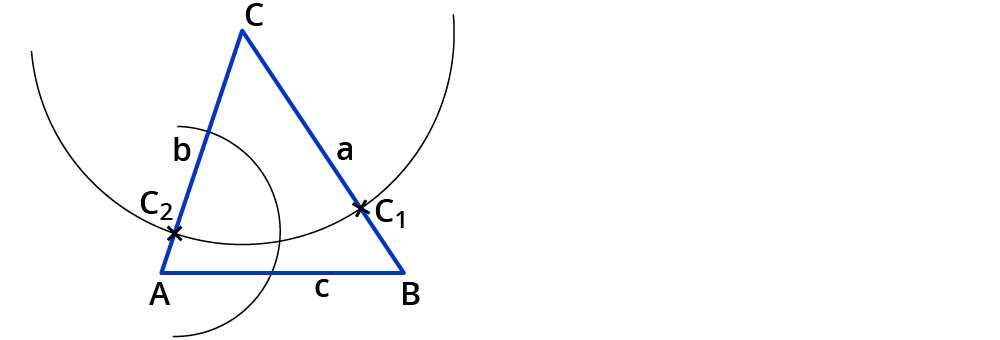



Zeichne mit derselben Zirkelspanne einen Kreisbogen um `C_1`.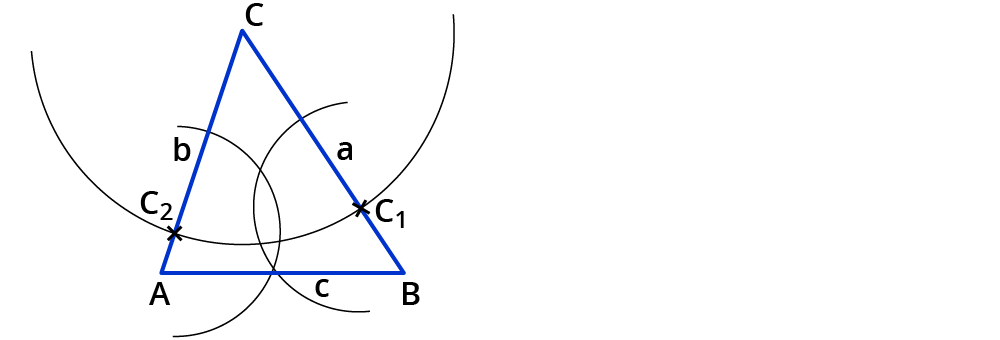



Du erhältst einen Schnittpunkt der Kreisbögen.

Endspurt

3. Schritt:
Verbinde den Schnittpunkt mit dem Eckpunkt `C` mithilfe eines Lineals.

Du hast die Winkelhalbierende des Winkels `gamma` konstruiert.
Bezeichne sie mit `w_gamma`.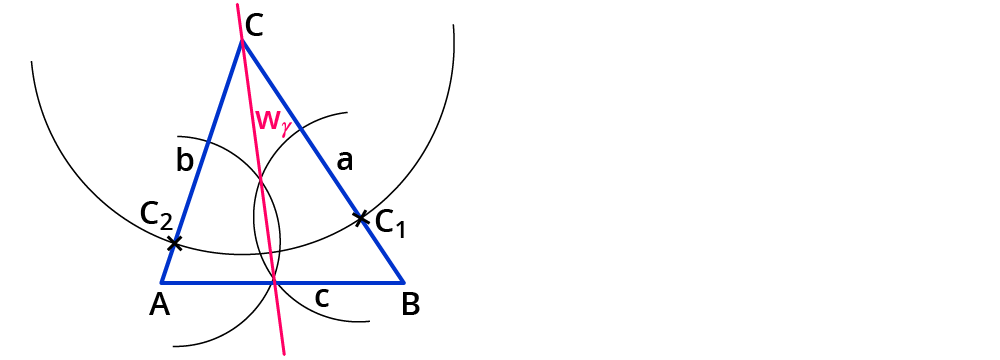

So konstruierst du den Inkreis

1. Schritt:
Wenn du alle Winkelhalbierenden des Dreiecks konstruiert hast, so erhältst du den Schnittpunkt `W`.

Dieser Punkt `W` ist gleichzeitig der Mittelpunkt des Inkreises des Dreiecks.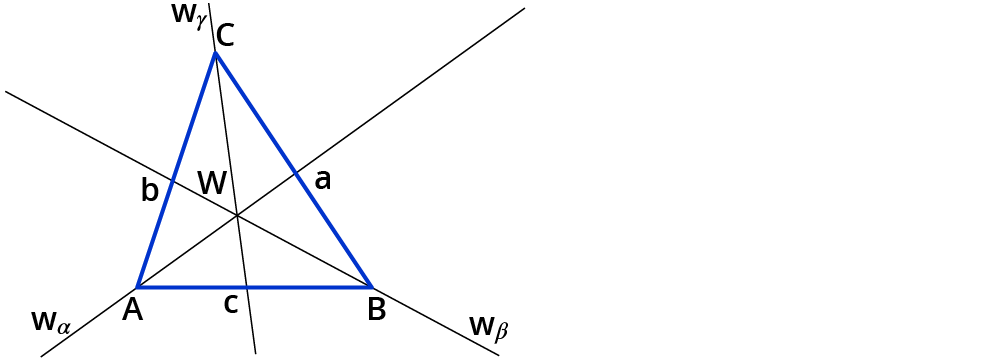



2. Schritt:
Stich mit der Zirkelspitze in den Punkt `W` ein und zeichne einen Kreisbogen, sodass dieser die Seite `a` zweimal schneidet.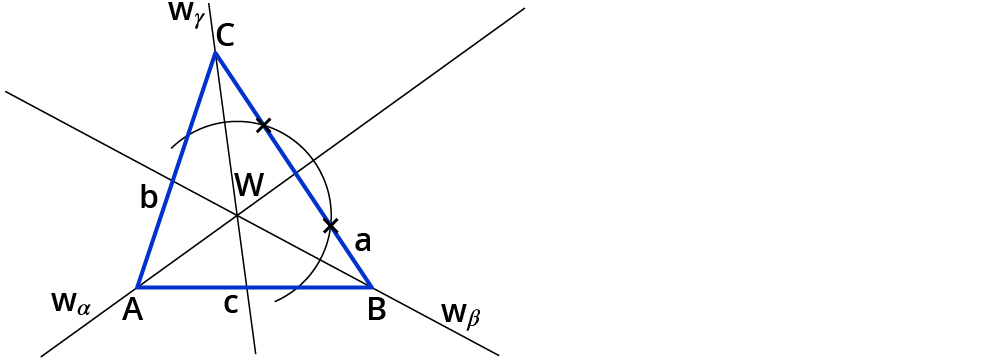



Du kannst auch die Seite `b` oder `c` wählen.

Das Ziel ist in Sicht

3. Schritt:
Stich mit der Zirkelspitze jeweils in die Schnittpunkte des Kreisbogens mit der gewählten Seite ein und zeichne je einen erneuten Kreisbogen mit dem gleichen Radius.

Du erhältst wieder zwei Schnittpunkte der Kreisbögen.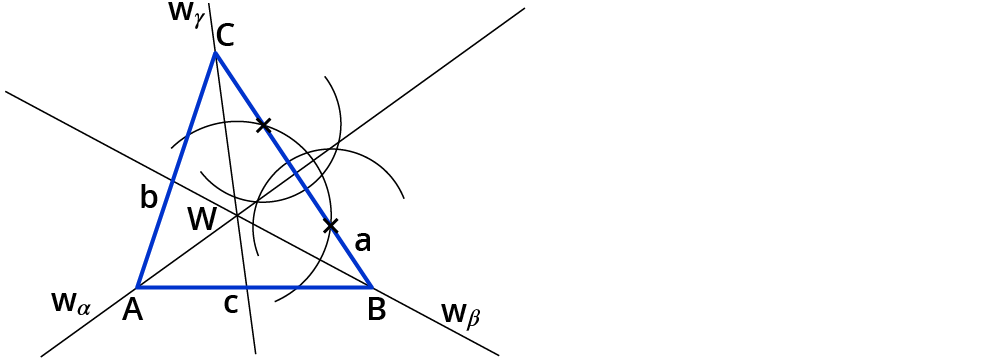

4. Schritt:
Verbinde die Schnittpunkte der Kreisbögen miteinander.

Du erhältst einen Schnittpunkt `K` mit der Seite und der entstandenen Geraden.

Den Schnittpunkt `K` verbindest du mit dem Punkt `W`.

Du hast den Radius des Inkreises konstruiert.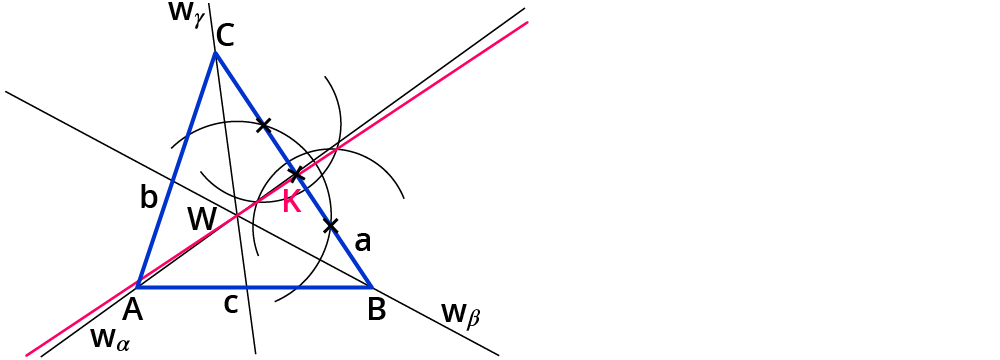

Der letzte Schritt

5. Schritt:
Stich mit der Zirkelspitze in den Punkt `W` ein.

Nimm als Zirkelspanne den Radius des Inkreises, also den Abstand zwischen dem Punkt `W` und Punkt `K`.

Zeichne um `W` herum einen vollständigen Kreis.

Wenn du richtig gezeichnet hast, berührt der Kreis jede Seite des Dreiecks.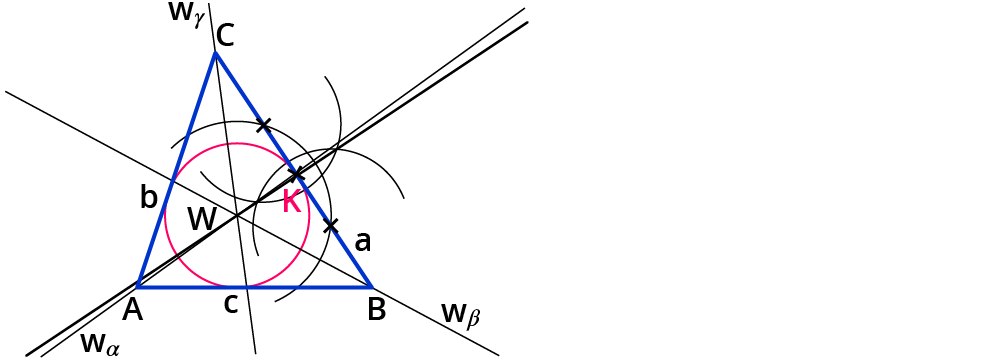



Und fertig: Du hast den Inkreis eines Dreiecks konstruiert!