Anwendungsaufgaben mit Dreiecken
Begründen mit Dreiecken
Wenn du die Eigenschaften von Dreiecken gut im Kopf hast, kannst du einen Schritt weitergehen und argumentieren und begründen.
Hier die wichtigsten Eigenschaften im Überblick:
- gleichschenklig: 2 Seiten gleich lang
- gleichseitig: 3 Seiten gleich lang, alle Winkel gleich groß
- Innenwinkelsumme: $$alpha + beta + gamma = 180^°$$
- Außenwinkelsumme: $$alpha´ + beta´ + gamma´ = 360^°$$
Beispiel:
Kann ein rechtwinkliges Dreieck 3 gleiche Seiten haben?
Antwort mit Begründung:
Die Winkel in einem gleichseitigen Dreieck sind alle gleich groß. In einem Dreieck beträgt die Innenwinkelsumme 180°. Jeder Winkel in einem gleichseitigen Dreieck ist daher 60° groß. Ein rechtwinkliges Dreieck kann also kein gleichseitiges Dreieck sein.
Für solche Aufgaben musst du gar nichts rechnen, aber viele Begriffe im Kopf haben und wissen, was sie bedeuten. Dann bist du fit fürs Argumentieren und Begründen!
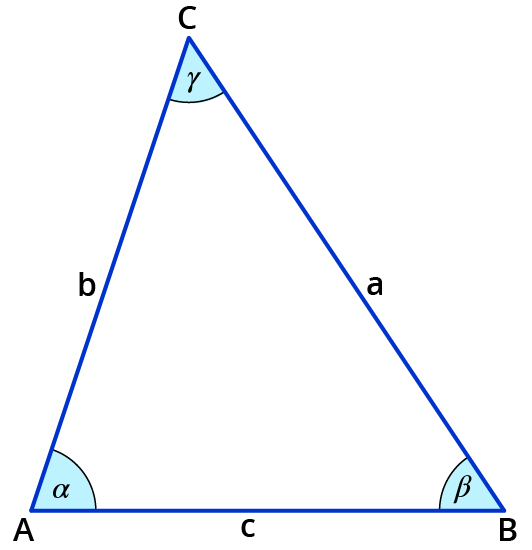
Dreiecksungleichung
Mit welchen Seitenlängen kommt überhaupt ein Dreieck zustande? Das entscheidest du mit der Dreiecksungleichung.
In einem Dreieck gilt: Addierst du die Länge von zwei Seiten eines Dreiecks, ist das Ergebnis größer als die Länge der dritten Seite.
$$a + b gt c$$ und $$a+c gt b$$ und $$b+c gta$$
Gehe so vor:
- Schritt: Prüfe mit Seitenlängen, ob die 3 Ungleichungen gelten.
- Schritt: Wenn ja, ergeben die Seitenlängen ein Dreieck. Wenn nein, gibt es das Dreieck nicht.
Der Alltag lässt nicht auf sich warten
Für Situationen aus dem Alltag benötigst du dein Wissen über die besonderen Linien im Dreieck. Meistens sind 3 Punkte gegeben (3 Bäume, 3 Städte) und du suchst einen bestimmten Punkt, der in Beziehung zu den 3 gegebenen Punkten steht.
Das sind alle besonderen Linien im Überblick:
- Der Schnittpunkt der 3 Mittelsenkrechten ist der Mittelpunkt des Umkreises.
- Der Schnittpunkt der 3 Winkelhalbierenden ist der Mittelpunkt des Inkreises.
- Der Schnittpunkt der 3 Seitenhalbierenden ist der Schwerpunkt des Dreiecks.
- (Der Schnittpunkt der 3 Höhen hat keine besonderen Eigenschaften.)
Umkreis: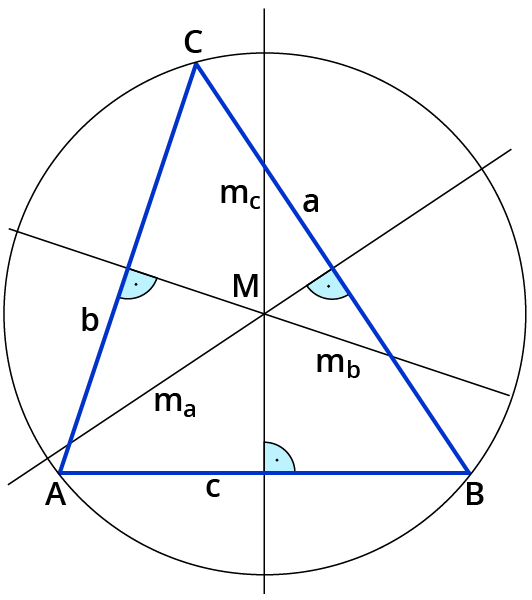
Inkreis: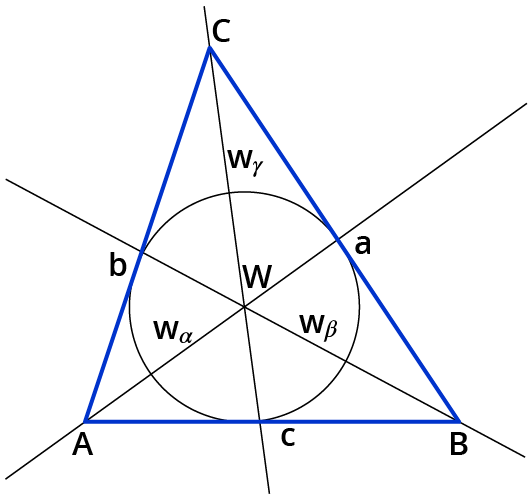

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



