Im echten Leben…

Im Alltag gibt es viele Situationen, in denen Maler, Gärtner, Fliesenleger Flächen berechnen. So wissen sie, wie viel Material sie brauchen und wie teuer das wird.

Die meisten Flächen sind ja Rechtecke oder Quadrate, von denen kannst du schon selbst Umfang und Flächeninhalt berechnen.

Beispiele:

• Der Küchenfußboden soll neue Fliesen bekommen.
• Ein Garten soll mit Rollrasen ausgelegt werden.
• Die Wände einer Wohnung sollen gestrichen werden.
• Das Dach eines Hauses soll neu gedeckt werden.

Neu gestrichen

Tobis Zimmer soll neu gestrichen werden. Er wünscht sich gelb als Farbe, wie die Farbe seines Lieblingsvereins.
Seine Mutter und er gucken auf der Internetseite des Baumarkts, wie viel die gelbe Farbe kostet. Sie lesen:

• Ein Liter Farbe reicht für 10 m².
• Die Farbe gibt es in 2-Liter-Eimern.
• Ein Farbeimer kostet 20 €.

Das ist der Grundriss von Tobis Zimmer:

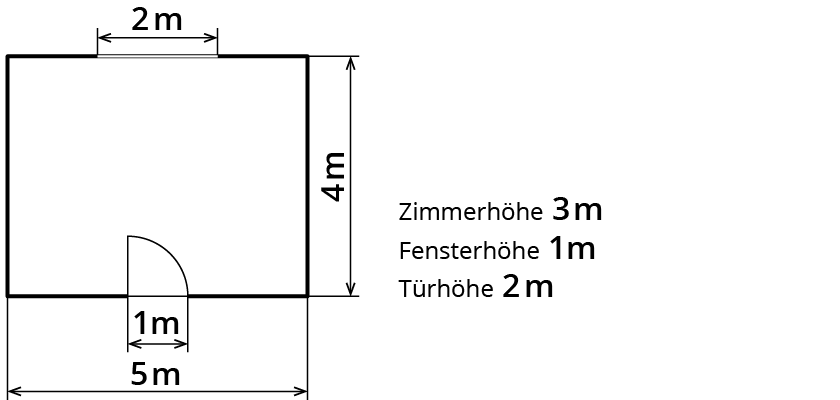
Das Zimmer ist 3 m hoch.

Jede Wand ist ein Rechteck.

Aber du siehst bestimmt schon die Schwierigkeit: Du kannst nicht einfach Seite mal Seite rechnen, denn da sind ja noch Fenster und Türen.
Fenster und Türen sind aber auch wieder Rechtecke, deren Flächen du berechnen kannst.

Die Fläche

Zunächst muss bestimmt werden, wie viel Quadratmeter gestrichen werden müssen.
Dazu berechnet man die Zimmerwände einzeln. Die farbige Markierung unten zeigt dies.

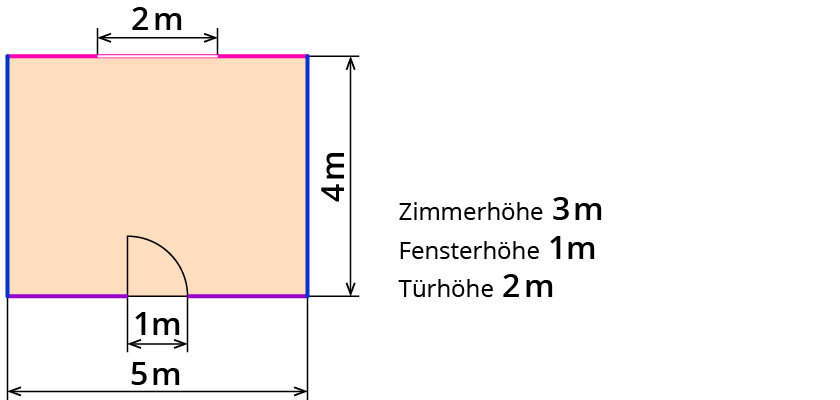
eine Seitenwand
A$$ = $$Breite$$*$$Zimmerhöhe$$ = $$4 m$$*$$3 m$$ = $$12 m²

Fensterseite:
A$$ = $$Länge$$*$$Zimmerhöhe$$-$$Fensterfläche
$$=$$5 m$$*$$3 m $$ – $$2 m$$*$$1 m$$ = $$15 m² $$– $$2 m²$$ = $$13 m²

Türseite:
A$$ = $$Länge$$*$$Zimmerhöhe$$ – $$Türfläche
$$ = $$5 m$$*$$3 m $$ – $$1 m$$*$$2 m$$ = $$15 m² $$ – $$2 m²$$ = $$13 m²

Deckenfläche nicht vergessen:
A$$ = $$Breite$$*$$Länge$$ = $$5 m$$*$$4 m$$ = $$20 m²

Gesamtfläche:
A$$ = $$ 2$$*$$12 m² $$ + $$ 13 m² $$ + $$ 13 m² $$+$$ 20 m² $$=$$ 70 m²

Farbeimer und Kosten

Du hast die Fläche berechnet, für die Tobi Farbe braucht: 70 m². Wie viel Farbeimer braucht Tobi? Wie viel kostet die Farbe?

Hier nochmal die Infos zu den Farbeimern:

• Ein Liter Farbe reicht für 10 m².
• Die Farbe gibt es in 2-Liter-Eimern.
• Ein Farbeimer kostet 20 €.

Also: Für 70 m² (7$$*$$10 m²) bräuchte Tobi 7 Liter.

Wie viel Farbeimer sind das?
2 Liter $$rarr$$ 1 Farbeimer
4 Liter $$rarr$$ 2 Farbeimer
6 Liter $$rarr$$ 3 Farbeimer
8 Liter $$rarr$$ 4 Farbeimer

Tobis Mutter kauft 4 Farbeimer. 3 Farbeimer wären zu wenig, die reichen nur für 60 m².

4 Farbeimer$$*$$20 €$$ = $$80 €.

Antwortsatz:
In Tobis Zimmer ist die Fläche, die gestrichen werden soll, 70 m² groß. Dazu braucht Tobi etwas mehr als 7 Liter Farbe. Er braucht 4 Farbeimer. Das kostet 80 €.

Tipps und Tricks

Jede Anwendungsaufgabe ist ein bisschen anders. Aber diese Punkte helfen dir, wenn du Anwendungsaufgaben löst:

• Bestimme, was gegeben und was gesucht ist.
• Stell dir die Aufgabe in der Wirklichkeit vor. Du kannst dir dazu eine Skizze zeichnen.
• Teile die Aufgabe in kleine Schritte ein, die du gut einzeln lösen kannst.
• Oft rundest du bei Anwendungsaufgaben auf, weil du meistens die nächstgrößere Packung oder so brauchst.
• Schreibe zum Schluss einen Antwortsatz und schaue, ob die Lösung Sinn macht.