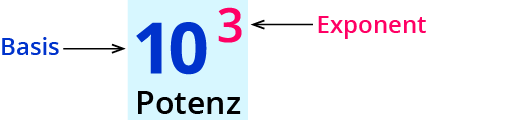Potenzen mit ganzzahligen Exponenten
Negative Hochzahlen
Sehr kleine Zahlen stellst du mit Potenzen mit negativen Hochzahlen dar.
Es gilt $$1/(10^2)=10^(-2)$$.
Aber die Basis muss nicht 10 sein. Genauso kannst du schreiben:
$$1/(2^2)=2^(-2)$$
$$1/(3^2)=3^(-2)$$
$$1/(5^3)=5^(-3)$$
Steht im Zähler eines Bruchs eine 1 und im Nenner eine Potenz $$a^n$$, so kannst du diesen Bruch als Potenz mit negativer Hochzahl schreiben:
$$1/a^n=a^(-n)$$
Zur Erinnerung einige Zehnerpotenzen:
…
$$1000 =10^3$$
$$100 =10^2$$
$$10 =10^1$$
$$1= 10^0$$
$$0,1= 1/10=10^(-1)$$
$$0,01= 1/10^2=10^(-2)$$
$$0,001= 1/10^3=10^(-3)$$
…
Ein paar Besonderheiten
$$3^1=3$$
$$3^0=1$$
$$5^0=1$$
$$0,2^0=1$$
$$3^(-1)=1/3$$
$$5^(-1)=1/5$$
Sowas gibt’s auch:
$$0,2^(-1)=1/0,2=5=5^1$$
Du weißt schon:
$$10^1=10$$
$$10^0=1$$ und
$$10^(-1)=1/10$$
Von der Potenz zum Bruch
Du kannst die Potenzen mit negativen Hochzahlen in Brüche umwandeln.
Beispiele:
$$3^(-3)=1/3^3=1/27$$
$$2^(-5)=1/2^5=1/(2*2*2*2*2)=1/32$$
$$2^3*3^(-2)=2^3*1/3^2=(2^3)/3^2=8/9$$

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Andersrum: Brüche in Potenzen umwandeln
Wenn im Nenner eine Potenz mit positivem Exponenten steht, kannst du den Bruch in eine Potenz übersetzen.
Beispiele:
$$1/16=1/2^4=2^(-4)$$
$$1/72=1/(8*9)=1/(2^3*3^2)=1/2^3*1/3^2=2^(-3)*3^(-2)$$
$$25/27=5^2/3^3=5^2*1/3^3=5^2*3^(-3)$$
Minuszeichen auch noch in der Basis
Auch beim Potenzieren brauchst du die Vorzeichenregeln.
Mit positiven Hochzahlen
$$(-3)^2=(-3)*(-3)=9$$
$$(-3)^3=(-3)*(-3)*(-3)=9*(-3)=-27$$
$$(-3)^4=(-3)*(-3)*(-3)*(-3)$$
$$=9*(-3)*(-3)=9*9=81$$
oder auch $$(-3)^4=(-3)^3*(-3)=(-27)*(-3)=81$$
Mit negativen Hochzahlen
$$(-3)^(-2)=1/(-3)^2=1/((-3)*(-3))=1/9$$
$$(-3)^-3=1/((-3)^3)=1/((-3)*(-3)*(-3))=1/(9*(-3))=-1/27$$
Auch für Potenzen mit negativer Hochzahl gilt:
Ist die Basis negativ, so ist die Potenz
- bei gerader Hochzahl positiv
- bei ungerader Hochzahl negativ.
Du weißt schon:
„Minus mal Minus ist Plus.“
Brüche als Basis
Klar, in der Basis können auch Brüche stehen.:-) Dann brauchst du die Multiplikations- und Divisionsregeln für Brüche.
Beispiele:
$$(1/2)^(-2)=1/((1/2)^2)=1/(1/2*1/2)=1/(1/4)=4$$
$$(2/3)^(-2)=1/((2/3)^2)=1/(2/3*2/3)=1/(4/9)=9/4$$
Multiplikation von Brüchen:
Regel: $$ ("Zähler mal Zähler") / (\text{Nenner mal Nenner $$
$$1/2*3/4=(1*3)/(2*4)=3/8$$
Division von Brüchen:
Du dividierst durch einen Bruch, indem du mit dem Kehrbruch multiplizierst.
$$1/2:3/4=1/2*4/3=(1*4)/(2*3)=4/6=2/3$$

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen