Zentrische Streckung - verkleinern und vergrößern

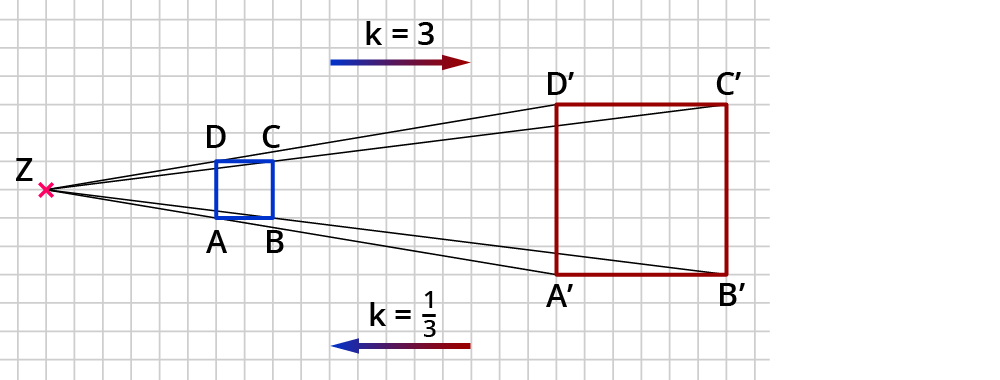
Auf der Abbildung siehst du ein Beispiel für zwei zentrische Streckungen.
Du glaubst es nicht? Dann schau genau hin.

Bei der ersten zentrischen Streckung wird das Quadrat $$ABCD$$ mit $$Z$$ als Zentrum und dem Streckungsfaktor $$k = 3$$ auf das Quadrat $$A’B’C’D’$$ abgebildet.

Bei der zweiten zentrischen Streckung wird das Quadrat $$A’B’C’D’$$ mit $$Z$$ als Zentrum und dem Streckungsfaktor $$k = frac{1}{3}$$ auf das Quadrat $$ABCD$$ abgebildet.

Der erste Fall ist ein Vergrößerung und der zweite Fall eine Verkleinerung.

Eigenschaften der zentrischen Streckung

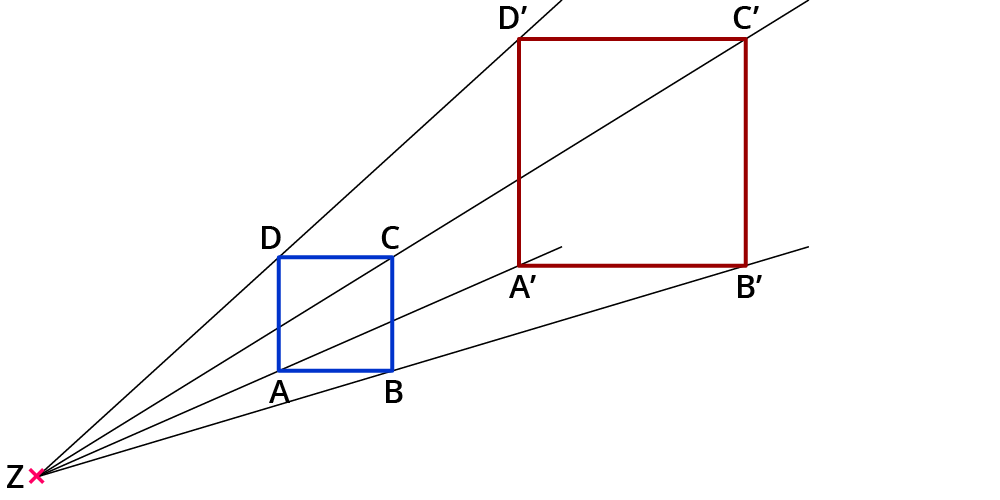
Hier hast du nochmal die Eigenschaften der zentrischen Streckung auf einen Blick:

1. Entsprechende Winkel in Figur und Bildfigur sind gleich groß - die zentrische Streckung ist winkeltreu.
2. Entsprechende Strecken in Figur und Bildfigur sind parallel.
3. Figur und Bildfigur sind einander ähnlich.
4. Jede Strecke $$bar(ZP)$$ wird auf eine $$k$$-mal so lange Strecke $$bar(ZP’)$$ abgebildet.
   
5. Der Streckfaktor $$k$$ folgt aus dem Längenverhältnis einander zugeordneter Strecken von Bildfigur und Figur:
   z.B. $$bar(ZA’) = k* bar(ZA)$$ oder $$bar(A’B’) = k* bar(AB)$$ oder $$bar(B’C’) = k* bar(BC)$$

Anwendung 1: Fotokopierer

Na, maulen deine Lehrer auch manchmal über die Kopierer an eurer Schule?:-)

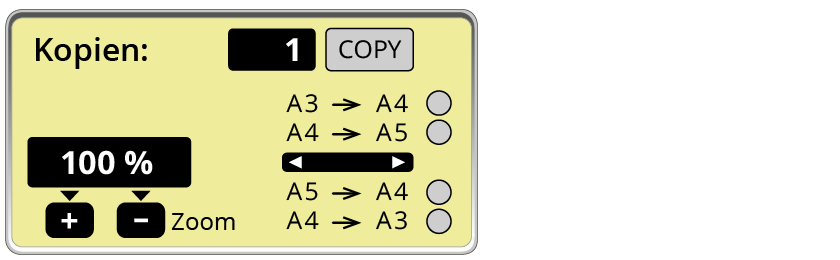
Dabei kannst du auch beim Kopieren Mathe betreiben:
Mit einem Fotokopierer können Dokumente oder Fotos vergrößert und verkleinert werden. Mithilfe der Tasten $$+$$ oder $$-$$ kannst du die gewünschte Größe über die Prozentzahl einstellen.

Durch die Größenveränderung einer Figur wird eine zentrische Streckung simuliert. Das Streckzentrum $$Z$$ bleibt unberücksichtigt, lediglich der Streckfaktor $$k$$ wird durch den Prozentsatz beschrieben.

Größeneinstellung

Ein Prozentsatz von größer 100% bedeutet, dass eine Figur mit dem Streckfaktor $$k gt 1$$ vergrößert wird.150 % bedeutet $$k = 1,5$$.

Ein Prozentsatz von kleiner 100 % bedeutet, dass eine Figur mit dem Streckfaktor $$0 lt k lt 1$$ verkleinert wird. 50 % bedeutet $$k = 0,5$$.

Beträgt der Prozentsatz 100 %, so bedeutet dies, dass die Größe der Figur erhalten bleibt. 100 % bedeutet $$k = 1$$.

Beispiel:
Eine quadratische Figur mit der Seitenlänge 16 cm wird mit einem Prozentsatz von 250% kopiert. Damit ist $$k = 2,5$$ und die Seitenlänge der Bildfigur beträgt $$2,5 * 16$$ $$cm = 40$$ $$cm$$.

Soll die Seitenlänge der Bildfigur 6,4 cm betragen, so ist wegen $$0,4 * 16$$ $$cm = 6,4$$ $$cm$$, also $$k = 0,4$$, der Zoomfaktor 40 %.

Bild: fotolia.com (Melisback)

Anwendung 2: DIN-Formate

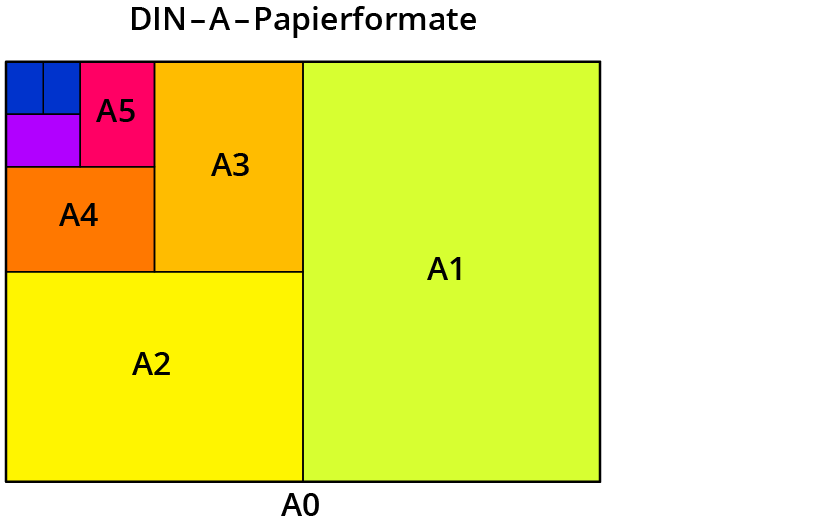
Das Papier, das in die Kopierer kommt, hat ja DIN-Formate wie A4 oder A3.
Am meisten benutzt du das DIN-A4-Format. Das hat die Breite 210 mm und die Höhe 297 mm.

Und was haben DIN-Formate mit der zentrischen Streckung zu tun?

DIN-Formate und zentrische Streckung

Die Fläche eines A0-Blattes beträgt
$$A = 841$$ $$mm * 1189$$ $$ mm = 999 949$$ $$ mm^2 approx 1$$ $$ m^2$$.

Faltest du ein A0-Blatt entlang seiner Breite, entstehen zwei A1-Blätter mit dem Flächeninhalt von je 0,5 m². Faltest du ein A1-Blatt wieder entlang seiner Breite, entstehen zwei A2-Blätter mit dem Flächeninhalt von je 0,25 m² usw.

Legst du die Blätter so übereinander, siehst du die zentrische Streckung: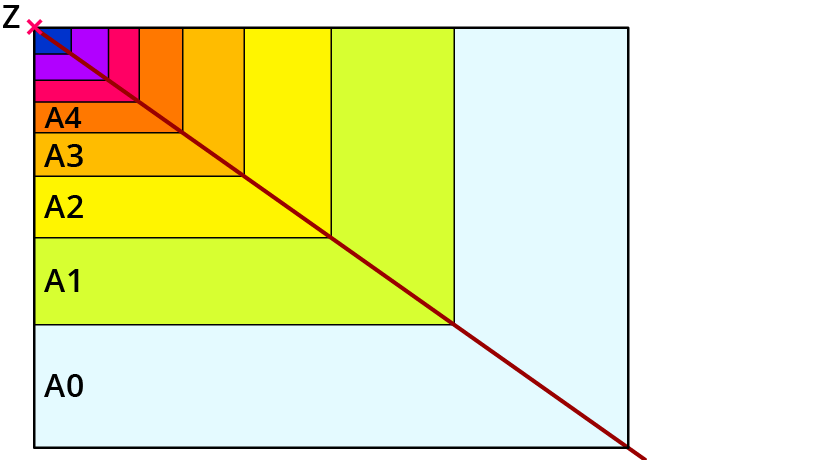



Die Rechtecke sind zueinander ähnlich.

Für Mathe-Freaks:

Das Seitenverhältnis $$a : b$$ eines beliebigen DIN-A-Blattes mit a als langer und b als kurzer Seite ist $$a : b = sqrt(2) : 1$$. Mit dieser Angabe und der Fläche für ein A0-Blatt lassen sich a und b eines beliebigen DIN-A-Blattes berechnen. Überprüfe dies für ein DIN-A5-Blatt.

Vergleiche dein Ergebnis mit diesen Werten für ein DIN-A5-Blatt:
Breite $$b = 148$$ $$mm$$ und Höhe $$a = 210$$ $$mm$$
Beachte: Der Übergang von DIN-A5 auf DIN-A4 bedeutet eine Vergrößerung mit dem Streckungsfaktor $$k = sqrt(2)$$, umgekehrt hat eine Verkleinerung von DIN-A4 auf DIN-A5 den Streckungsfaktor $$k = frac{1}{sqrt2}$$.
Diese Aussage gilt allgemein für alle benachbarten DIN-A-Formate.

Negative Streckfaktoren: $$k lt 0$$

Bisher hatte der Streckfaktor Werte $$k gt 0$$. Aber es gibt auch negative Streckfaktoren!

Für $$k lt 0$$ gilt, dass der Bildpunkt, z.B. $$P’$$, auf der Verlängerung der Strecke $$bar(ZP)$$ über $$Z$$ hinaus liegt. Hier siehst du Beispiele für $$k = - frac{1}{3}$$ und $$k = - 2$$
Im Vergleich dazu siehst du zentrische Streckungen mit den Streckfaktoren $$k = frac{1}{3}$$ und $$k = 3$$.

Aus der Abbildung kannst du auch entnehmen, dass für Streckfaktoren $$k$$ mit $$|k| gt 1$$ stets eine Vergrößerung erfolgt, mit $$|k| lt 1$$ dagegen stets eine Verkleinerung.

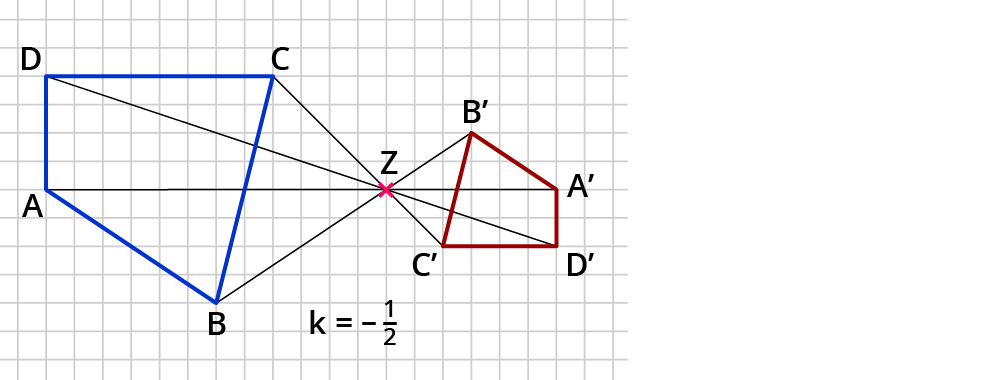
Beispiel: $$k = -frac{1}{2} , |k| lt 1$$

Der Storchschnabel oder Pantograph

Der Pantograph ist ein Zeichengerät, mit dem vor der Digitalisierung maßstabsgerechte Verkleinerungen bzw. Vergrößerungen durchgeführt wurden. Heute machen sowas Grafikprogramme.

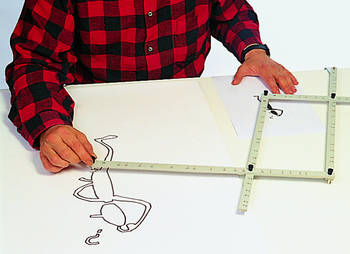
Bild: Torsten Warmuth

Konstruktion eines Pantographen

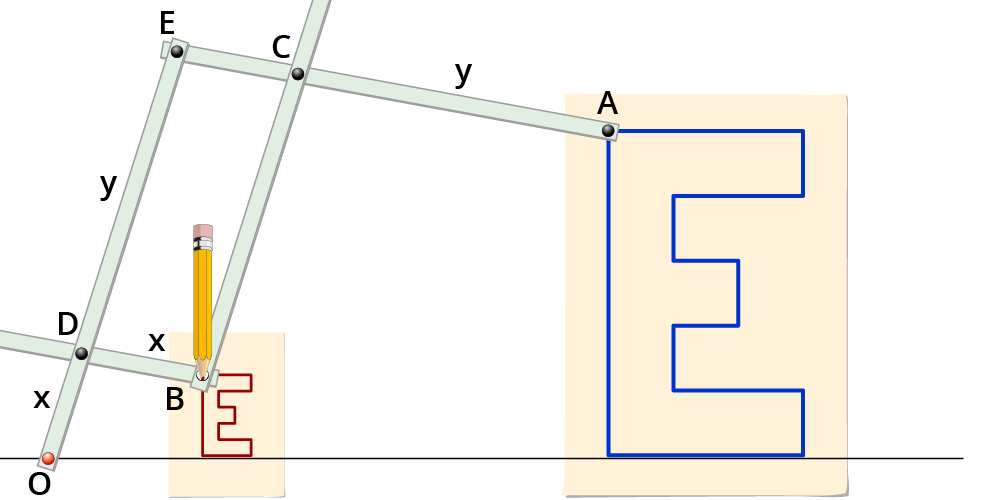
Es muss gelten:
$$bar(OE) = bar(EA) = y$$ und $$bar(OD) = bar(DB) = bar(EC) = x$$.
Das Viereck $$DBCE$$ ist ein Parallelogramm.

Hier siehst du den Aufbau und die Eigenschaften eines Pantographen. Nach diesem Bild kannst du dir selbst so ein Gerät bauen. Wähle Streben aus starker Pappe, Holz oder am besten Elementen eines Stabilbaukastens.

Halte den Pantographen am $$O$$ fest. Fahre mit einem Stift in $$A$$ die Umrisse der Figur ab. Hier ist die Figur ein großes E. Dann zeichnet ein Stift in $$B$$ die verkleinerte Bildfigur.
Wenn du die Figur in $$B$$ entlangfährst und die Bildfigur mit $$A$$ zeichnest, dann zeichnest du die vergrößerte Bildfigur.

Viel Spaß beim Ausprobieren!