Den Ähnlichkeitssatz für Dreiecke anwenden
Ähnliche Dreiecke
2 Dreiecke heißen „ähnlich zueinander“, wenn ihre Winkel identisch sind. Der Flächeninhalt und somit die Seitenlängen können aber durchaus verschieden sein. Ähnliche Dreiecke können auch gespiegelt vorliegen.
Oft kannst du per Augenmaß entscheiden, ob 2 Dreiecke ähnlich zueinander sind. Wenn das nicht ausreicht und du korrekt mathematisch arbeiten willst, gelten Bedingungen für die Ähnlichkeit.
Kongruenz und Ähnlichkeit
Erinnerst du dich noch an die Kongruenzsätze SSS, WSW, SWS und SsW? Du kannst sie auf die Ähnlichkeit von Dreiecken übertragen, denn auch hier gibt es verschiedene Ähnlichkeitssätze.
Wenn 2 Dreiecke kongruent zueinander sind, sind sie automatisch auch ähnlich zueinander.
2 Dreiecke sind kongruent, wenn sie
- in 3 Seiten übereinstimmen (SSS) oder
- in einer Seite und den anliegenden Winkeln übereinstimmen (WSW)
oder - in 2 Seiten und dem Winkel zwischen den Seiten übereinstimmen (SWS) oder
- in 2 Seiten und dem der längeren Seite gegenüberliegenden Winkel übereinstimmen (SsW).
Ähnlichkeitssatz WW
Der Ähnlichkeitssatz WW heißt:
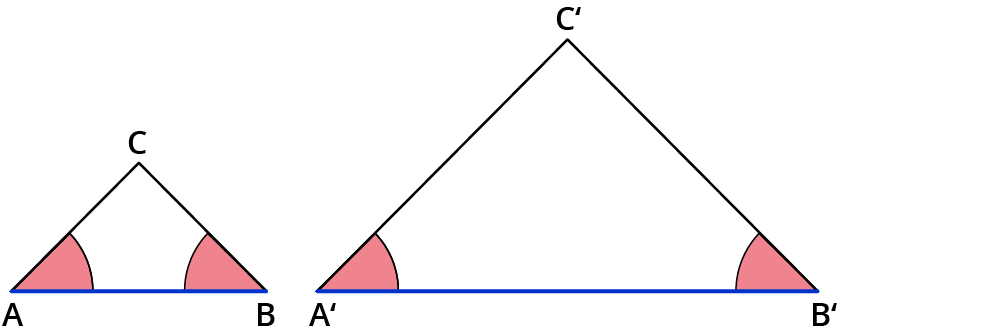
„Wenn 2 Dreiecke in 2 Winkeln übereinstimmen, dann sind sie ähnlich zueinander.“
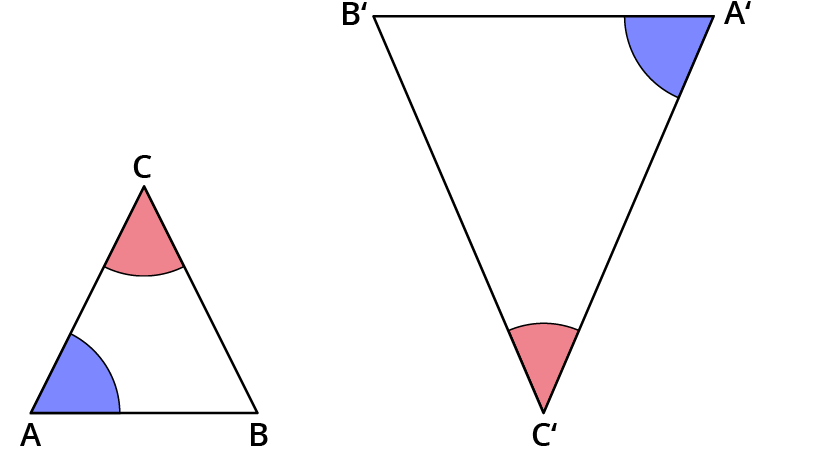
Diese Dreiecke sind ähnlich, wenn der rote Winkel gleich dem roten Winkel und der blaue Winkel gleich dem blauen Winkel ist.
Es ist nicht nötig, den dritten Winkel auch zu überprüfen, weil die Winkelsumme in jedem Dreieck 180° groß ist. Stimmen die ersten beiden Winkel überein, ist auch der dritte Winkel gleich groß.
Es gibt keinen Kongruenzsatz WWW zum Erzeugen von kongruenten Dreiecken: Dreiecke, die in ihren Winkeln übereinstimmen, müssen nicht denselben Flächeninhalt haben, sondern können auch gestreckt oder gestaucht sein.
Ähnlichkeitssatz SSS
2 Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen der Längen der Seiten übereinstimmen.
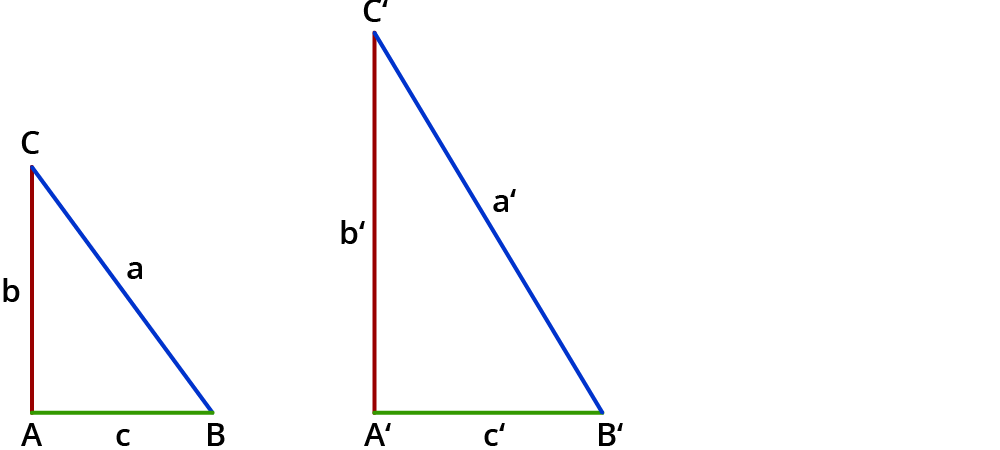
$$a/(a’)=b/(b’)=c/(c’)$$
Das Seitenverhältnis der roten Seiten ist gleich dem Seitenverhältnis der blauen Seiten ist gleich dem Seitenverhältnis der grünen Seiten.
Bei den Ähnlichkeitssätzen betrachtest Du immer das Seitenverhältnis, bei den Kongruenzsätzen die Seitenlängen!

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Ähnlichkeitssatz SWS
2 Dreiecke sind zueinander ähnlich, wenn sie in 2 Längen der Seitenverhältnisse und dem eingeschlossenen Winkel übereinstimmen.
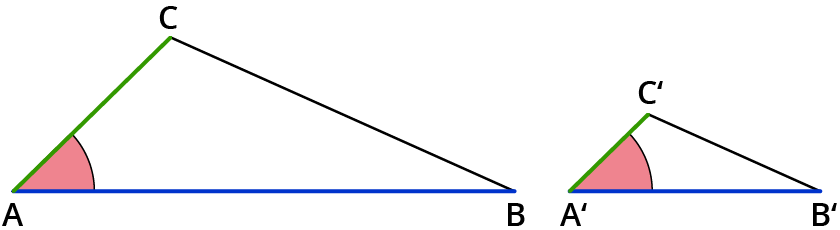
Hier stimmt das Seitenverhältnis der blauen Seiten mit dem Seitenverhältnis der grünen Seiten überein. Der rote Winkel ist identisch.
Oder auch:
$$b/(b’)=c/(c’)$$ und $$alpha=alpha’$$
Das W steht absichtlich zwischen den S-Buchstaben. Es soll dich erinnern, dass der Winkel von beiden Seiten eingerahmt ist.
Ähnlichkeitssatz SsW
2 Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis der Längen zweier Seiten und im Gegenwinkel der längeren Seite übereinstimmen.
$$b/c=(b’)/(c’)$$ $$gamma=gamma’$$
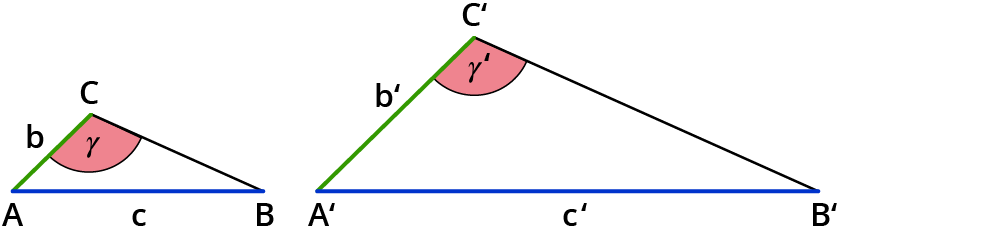
$$gamma$$ liegt bei diesen Dreiecken gegenüber der längsten Seite und liegt an der Seite $$b$$ an.
Ähnlichkeitssatz WSW?
Bei den Kongruenzsätzen gibt es auch den Kongruenzsatz WSW.
Der Satz besagt, 2 Dreiecke sind kongruent, wenn sie in 2 Winkeln und der eingeschlossenen Seite übereinstimmen.
Einen Ähnlichkeitssatz WSW gibt es nicht, denn er enthält eine unnötige Information. Als ersten Ähnlichkeitssatz hast du den Ähnlichkeitssatz WW kennen gelernt. 2 Dreiecke sind ähnlich zueinander, wenn sie in 2 Winkeln übereinstimmen. Die Seite S musst du nicht mehr überprüfen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beweis für den Ähnlichkeitssatz SWS
Du gehst für den Beweis für den Ähnlichkeitssatz SWS davon aus, dass du 2 Dreiecke gegeben hast, für die folgendes gilt:
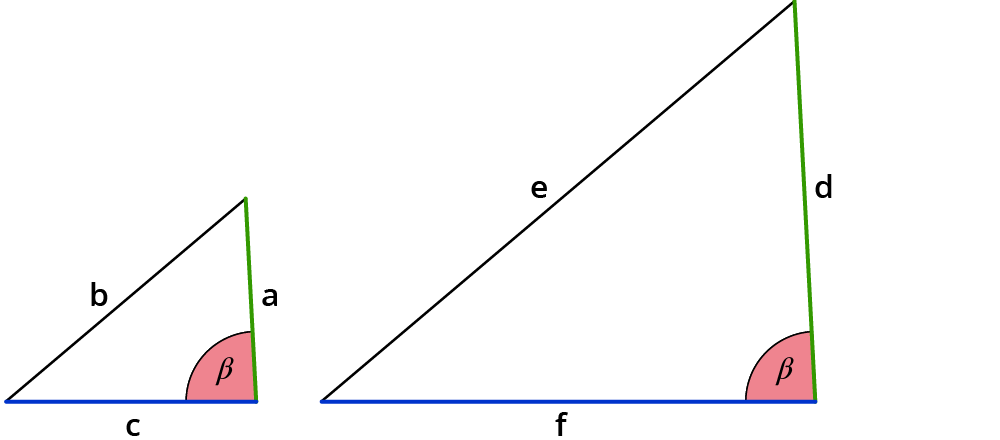
Der Winkel $$beta$$ ist identisch.
Die Seitenlängen liegen in demselben Verhältnis vor. Aus diesem Verhältnis ergibt sich ein Faktor $$k$$.
$$f/c=d/a=k$$
Es gibt ein zweites Dreieck, das aus dem Dreieck mit den Seiten $$a$$, $$b$$ und $$c$$ durch zentrische Streckung mit dem Faktor $$k$$ im Punkt $$B$$ hervorgegangen ist.
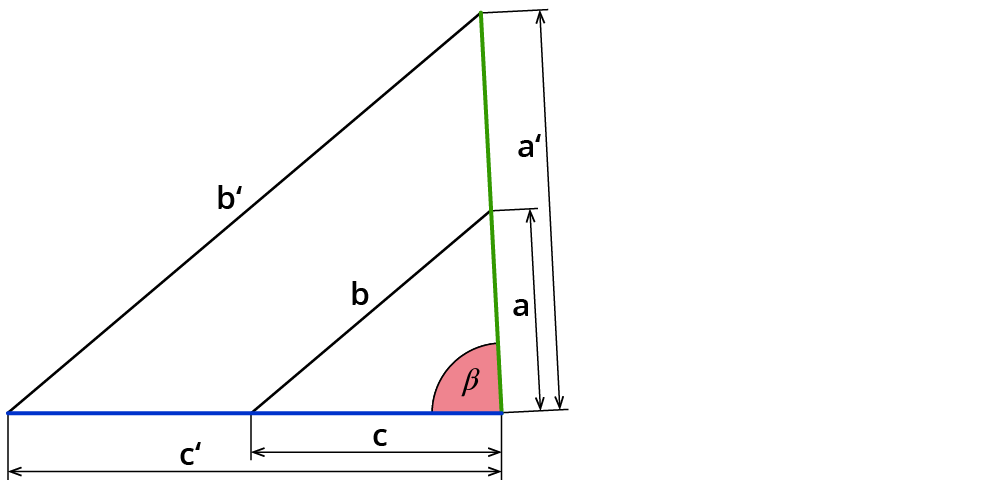
Für dieses Bilddreieck gilt
$$a’=k*a$$, also die Seite $$a’$$ hat dieselbe Länge wie $$k*$$ die Seite $$a$$.
$$k*a$$ ist auch gleich der Länge der Seite $$d$$. Also ist $$a’=d$$. Genauso kannst du zeigen, dass $$c’=f$$ ist.
Das Bilddreieck mit den Seiten $$a’,b’,c’$$ ist demnach kongruent zum Dreieck mit den Seiten $$d$$, $$e$$, $$f$$, denn hier gilt der Kongruenzsatz SWS.
Die Dreiecke mit den Seiten $$a$$, $$b$$, $$c$$ und $$d$$, $$e$$, $$f$$ sind somit ähnlich.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



