Ein Ausflug in die Optik

Stell dir vor, du nimmst eine Taschenlampe und wirfst den Schatten einer Figur an die Wand. Das sieht ungefähr so aus:

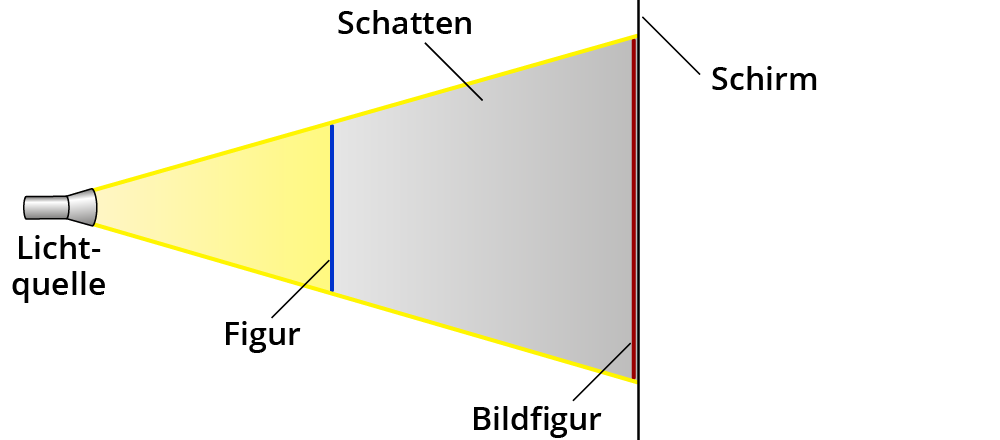
Physiker würden sagen: Eine punktförmige Lichtquelle erzeugt von einem Gegenstand auf einem Schirm einen scharf begrenzten Schatten.
Der Schatten ist das Bild oder die Bildfigur. Als Begrenzungslinien siehst du zwei Lichtstrahlen.

Du erkennst, dass die Figur bei dieser Konstruktion vergrößert wird.
Physiker nennen das Abbildungsgesetz. Du lernst hier die Mathematik dahinter. Dazu brauchst du die zentrische Streckung.

Zentrische Streckung

Mit der zentrischen Streckung kannst du maßstabsgerechte Figuren herstellen. Mit dem Computer geht das heute ganz einfach mit Bildbearbeitungsprogrammen.

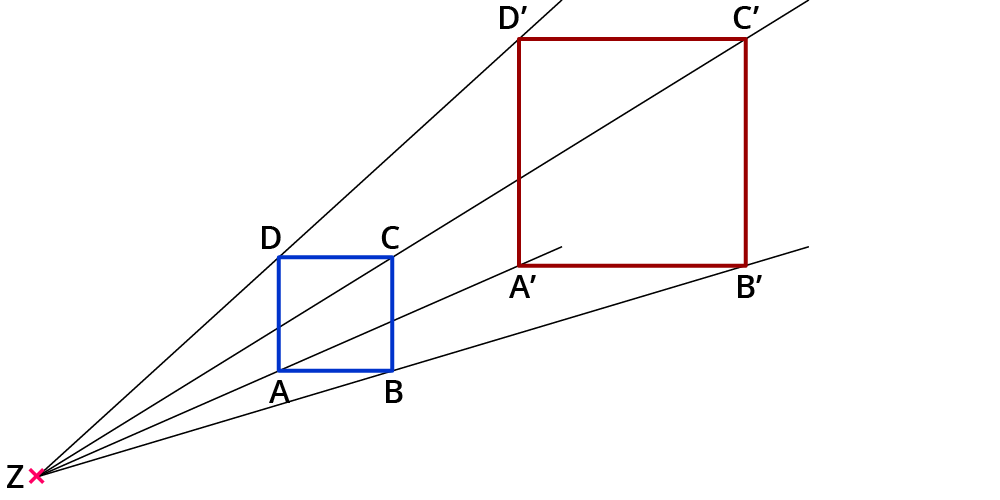
Was macht eine zentrische Streckung aus?

Sie bildet eine Figur auf eine ähnliche Bildfigur ab:

1. Winkel bleiben gleich ( Winkeltreue ).
2. Parallele Strecken bleiben parallel .

Jede Strecke $$bar(ZA)$$ entspricht dabei einer $$k$$-mal so langen Strecke $$bar(ZA’)$$.

Der Streckfaktor $$k$$ folgt aus dem Längenverhältnis einander zugeordneten Strecke von Bildfigur und Figur:
z.B. $$bar(ZA’) = k* bar(ZA)$$ oder $$bar(A’B’) = k* bar(AB)$$ oder $$bar(B’C’) = k* bar(BC)$$.

So geht’s

Führe eine zentrische Streckung mit dem Faktor 2 durch.

Zeichne einen Strahl von $$Z$$ aus durch einen Punkt $$A$$.
Trage die Strecke $$bar(ZA)$$ von $$Z$$ aus zweimal auf dem Strahl ab. Du erhältst den Punkt $$A’$$.

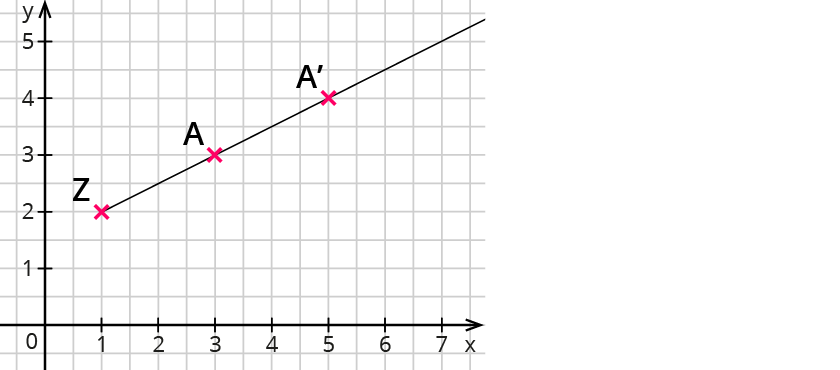
Es gilt: $$bar(ZA’) = 2 * bar(ZA)$$.

Zentrische Streckung eines Dreiecks $$ABC$$

Bei einem Dreieck machst du das ganze dreimal. Mit den Punkten des Dreiecks $$ABC$$ konstruierst du mit dem Streckfaktor k=2 die Bildpunkte $$A’, B’$$ und $$C’$$. Verbinde die Punkte zum Bilddreieck $$A’B’C’$$.

Jetzt bist du dran

Konstruiere in einem Koordinatensystem das Dreieck $$ABC$$ und zeichne das Streckzentrum $$Z$$ ein. Führe dann eine zentrische Streckung mit dem Streckfaktor k durch.
Gegeben: $$A(2|1), B(4|4), C(3|5), Z(0|2), k = 1,5$$

Lösung

Eigenschaften der zentrischen Streckung

Hier hast du die Eigenschaften der zentrischen Streckung auf einen Blick:

1. Die sich entsprechenden Winkel in Figur und Bildfigur sind gleich groß. Die zentrische Streckung ist winkeltreu.
2. Entsprechende Strecken in Figur und Bildfigur sind parallel.
3. Figur und Bildfigur sind einander ähnlich.
4. Jede Strecke $$bar(ZP)$$ wird auf eine $$k$$-mal so lange Strecke $$bar(ZP’)$$ abgebildet.
   
5. Der Streckfaktor $$k$$ folgt aus dem Längenverhältnis einander zugeordneten Strecke von Bildfigur und Figur:
   z.B. $$bar(ZA’) = k* bar(ZA)$$ oder $$bar(A’B’) = k* bar(AB)$$ oder $$bar(B’C’) = k* bar(BC)$$

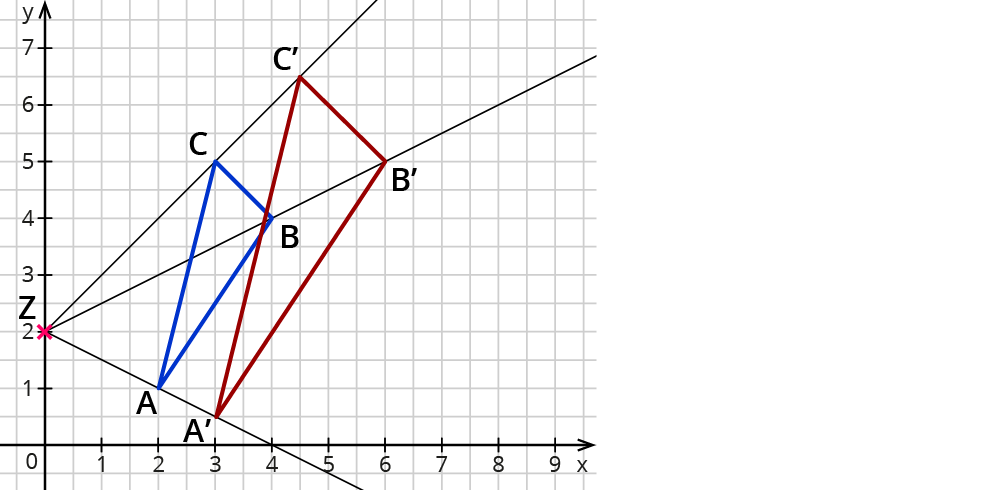
Bestimmen des Streckzentrums $$Z$$ und des Streckfaktors $$k$$

Gegeben sind das Dreieck $$ABC$$ und das Bilddreieck $$A’B’C’$$.

Bestimme die Koordinaten des Streckzentrums $$Z$$ und den Streckfaktor $$k$$.

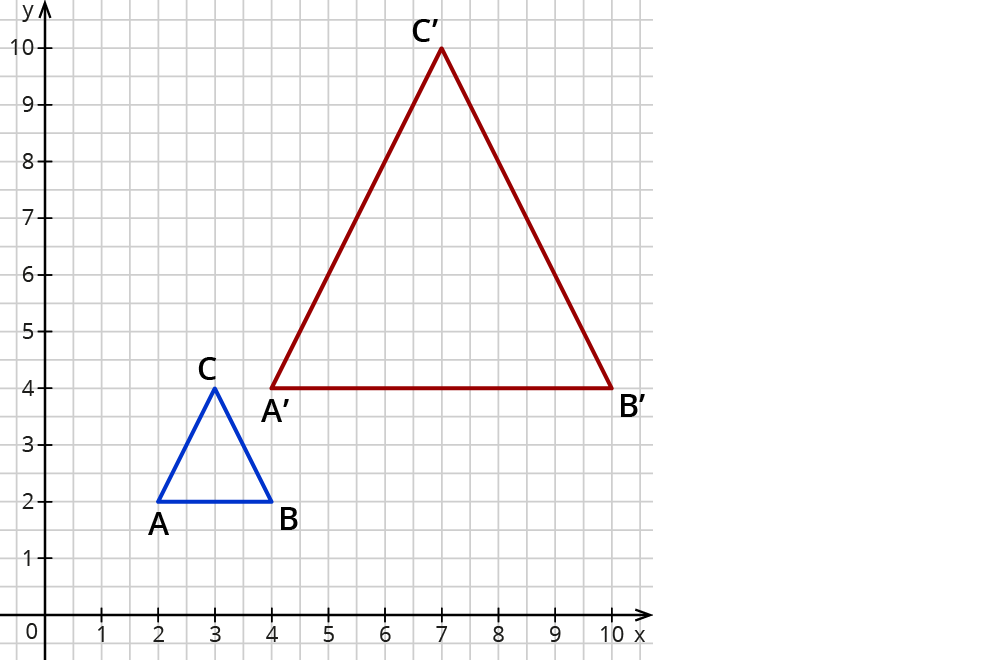
Lösung

Konstruiere durch die einander zugeordneten Punkte $$A, A’$$, $$B,B’$$ und $$C,C’$$ Geraden.
Schneiden sich die Geraden in einem Punkt, so ist dieser Punkt das Streckzentrum $$Z$$.
Aus dem Längenverhältnis einander zugeordneten Strecke kannst du den Streckfaktor $$k$$ bestimmen.

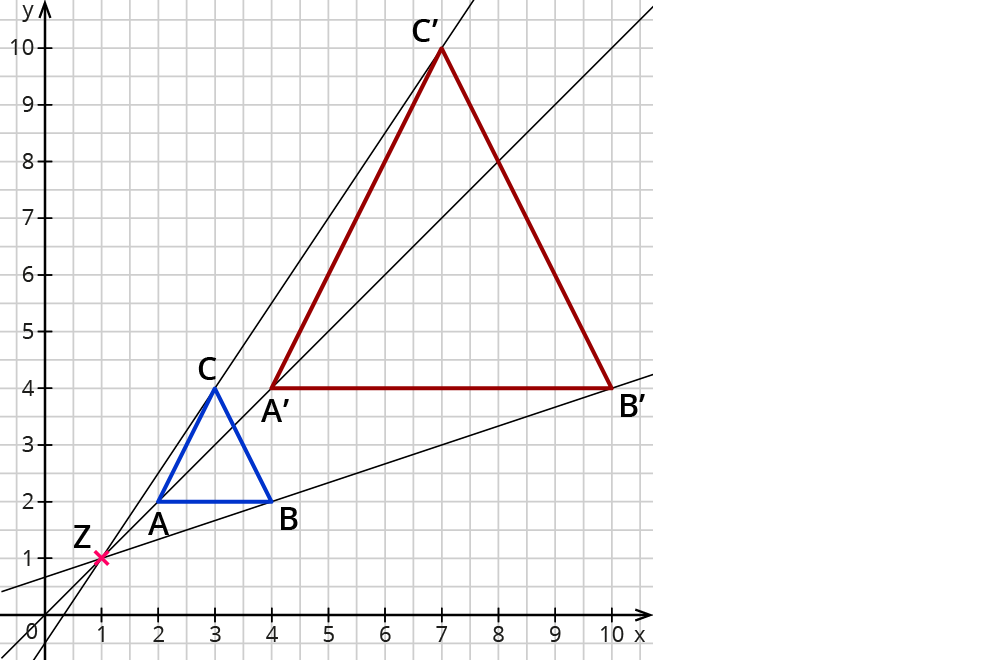
Streckzentrum:
$$Z(1|1)$$
Streckfaktor:
$$bar(A’B’) = 6$$ und $$bar(AB) = 2$$. Es gilt $$bar(A’B’) = k * bar(AB)$$.
Also ist der Streckfaktor $$k = 3$$.