Eigenschaften der Sinus- und Kosinusfunktion 3
Sinus- und Kosinusfunktion mit allen Parametern
Du kannst schon die Periodenlänge und die Amplitude der Sinus- und der Kosinusfunktion verändern. Das geht mithilfe der Parameter $$a$$ und $$b$$ in $$f(x)=a*sin(b*x)$$. Sie strecken bzw. stauchen die Funktion.
In der Realität kannst du so z.B. Änderungen des Wasserpegels in verschiedenen Küstengebieten richtig darstellen.
Das reicht aber noch nicht:
- Der Wasserstand schwankt nicht um 0 Meter wie die Sinusfunktion. Er kann zwischen 2 m bei Ebbe und 4 m bei Flut schwanken. Wie kannst du die Sinusfunktion nach oben und unten verschieben?
- Ebbe und Flut verschieben sich jeden Tag um wenige Minuten. Wie kannst du die Wellenberge im Koordinatensystem nach rechts oder links verschieben?
Verschieben… Na, dann mal los:
Ebbe und Flut im Hafen von Hamburg:
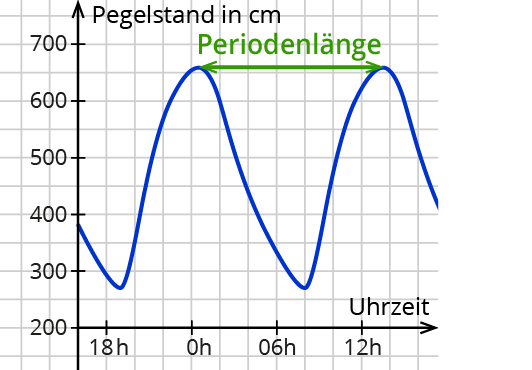
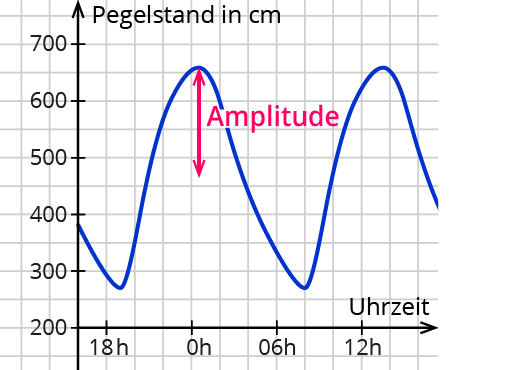
Nach oben und unten verschieben
Die Funktionswerte von $$f(x)=sin(x)$$ schwanken um die x-Achse und nehmen Werte zwischen $$-1$$ und $$+1$$ an.
Wie bekommst du einen Sinus-Graphen, der zwischen 0 und 2 schwankt? Verschiebe alle Funktionswerte um 1 nach oben. Rechnerisch: Addiere zu allen Funktionswerten 1.
Als Funktionsgleichung sieht das so aus: $$f(x)=sin(x)+d$$.
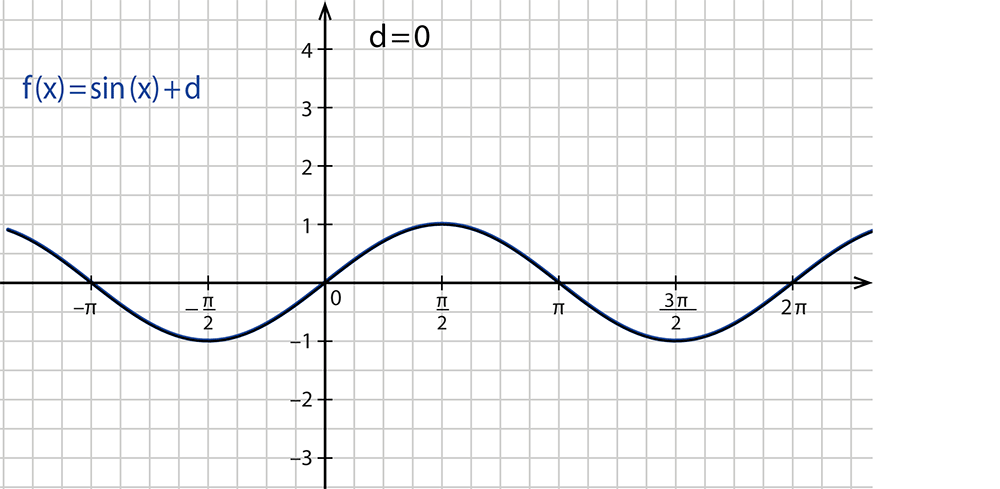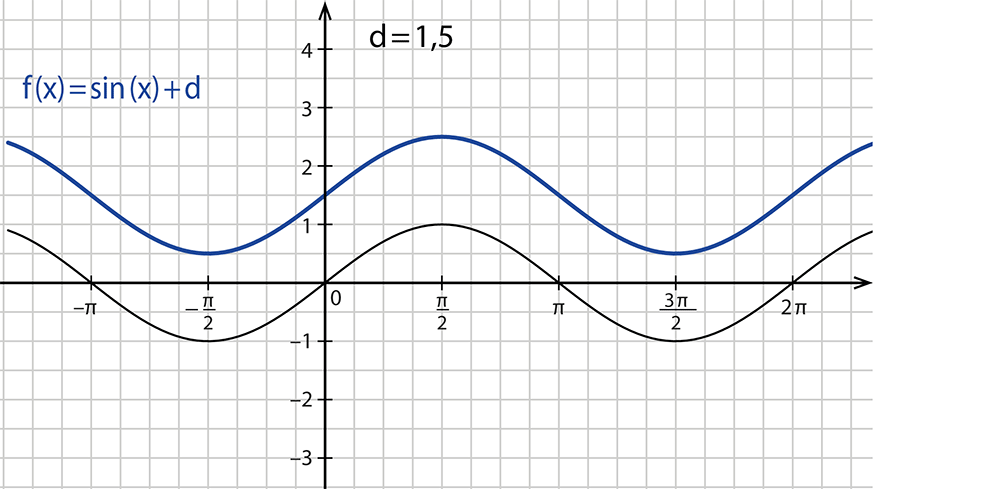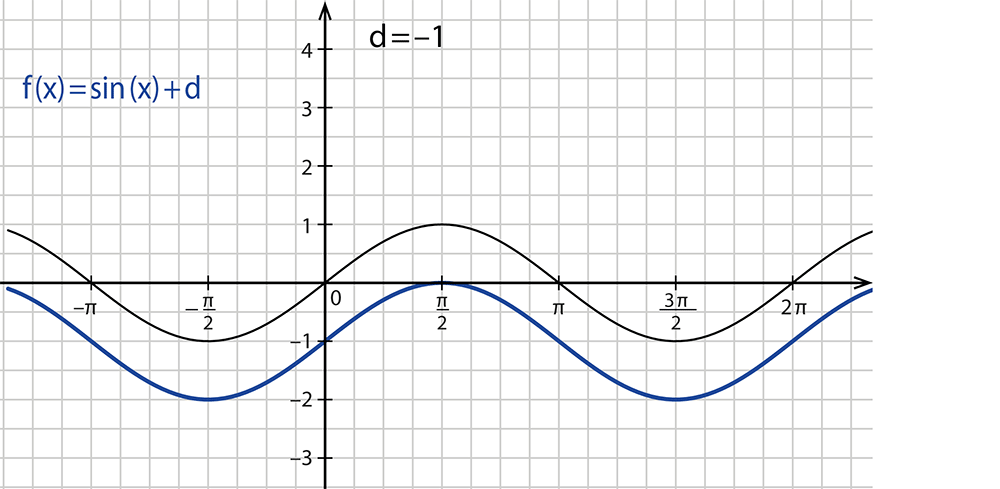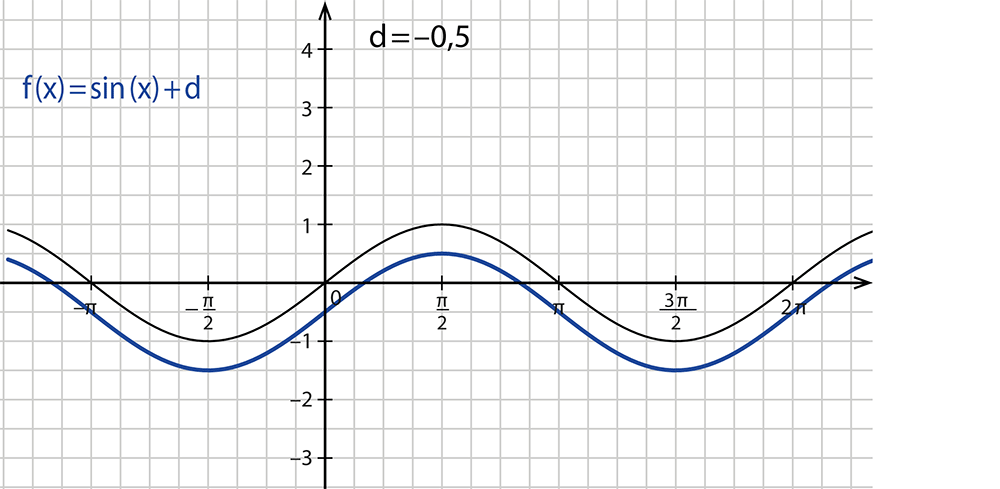
- Der Parameter $$d$$ verschiebt die Kurve in y-Richtung.
- Wenn $$d$$ größer als $$0$$ ist, ist die Sinusfunktion nach oben verschoben.
- Wenn $$d$$ kleiner als $$0$$ ist, ist die Sinusfunktion nach unten verschoben.
Für $$g(x)=cos(x)+d$$ funktioniert die Verschiebung in y-Richtung ganz genauso.
Nach rechts und links verschieben
Willst du die Kurve nach rechts oder links verschieben, so kannst du die gleiche Überlegung, die bereits auf der letzten Seite für die y-Werte getätigt wurde, auf die x-Werte anwenden.
$$f(x)=sin(x-c)$$
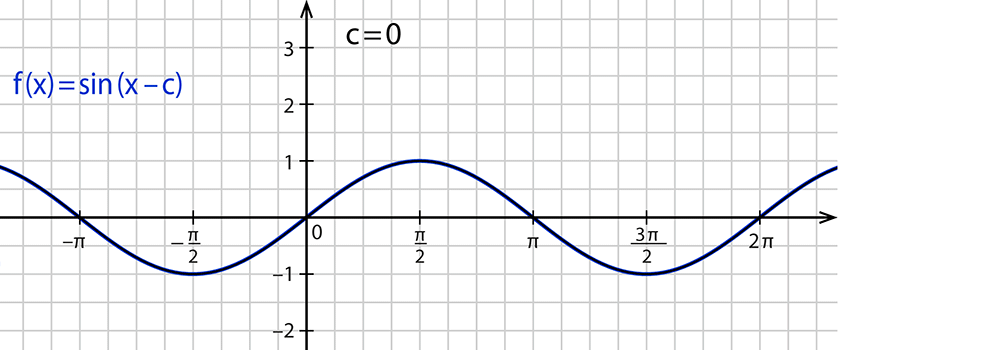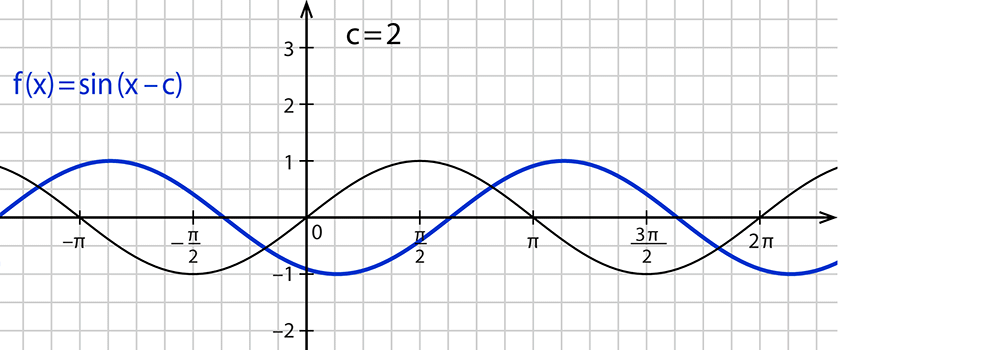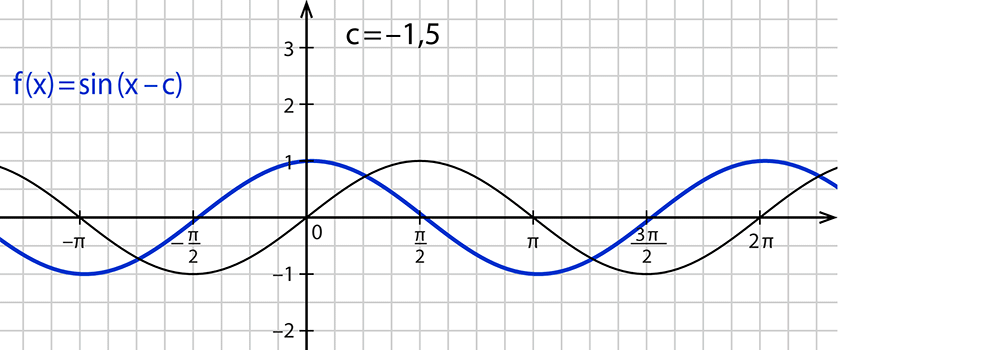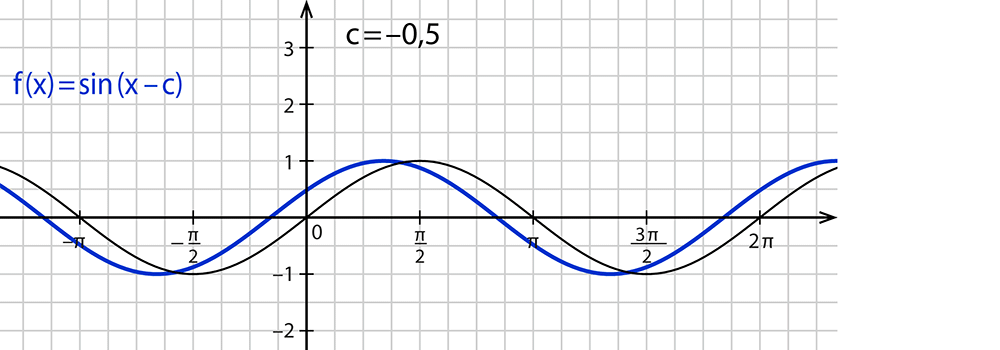
- Der Parameter $$c$$ in $$f(x)=sin(x-c)$$ verschiebt die Kurve in x-Richtung.
- Wenn $$c$$ größer als $$0$$ ist, ist die Sinusfunktion nach rechts verschoben.
- Wenn $$c$$ kleiner als $$0$$ ist, ist die Sinusfunktion nach links verschoben.
Wichtig: Beim Verschieben nach links und rechts ist wie beschrieben in $$f(x)=sin(x$$ $$-$$ $$c)$$ mit Minus in der Mitte. Manchmal wirst du als Funktionsgleichung $$f(x)=sin(x$$$$+$$$$c)$$ sehen, dann sind links/rechts genau umgekehrt.
Für $$g(x)=cos(x-c)$$ funktioniert die Verschiebung in x-Richtung ganz genauso.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Überblick über alle Parameter
Du ahnst, was jetzt kommt: alle Parameter $$a,$$ $$b,$$ $$c,$$ $$d$$ in einer Funktionsgleichung $$g(x)=a*sin(b*(x-c))+d$$! Nice!:-)
Beispiel:
$$g(x)=3*sin(2*(x-3/4pi))+4$$
- Die Amplitude des Graphen ist 3-mal so groß wie bei $$sinx$$.
- Die Wellenbewegung des Graphen ist 2-mal so schnell wie bei $$sin x$$. Das heißt: Die Periodenlänge ist nur halb so groß.
- Die Kurve ist um $$3/4 pi$$ in x-Richtung verschoben.
- Die Kurve ist um 4 in y-Richtung verschoben. Die Kurve schwankt um den Mittelwert 4 statt um die 0.
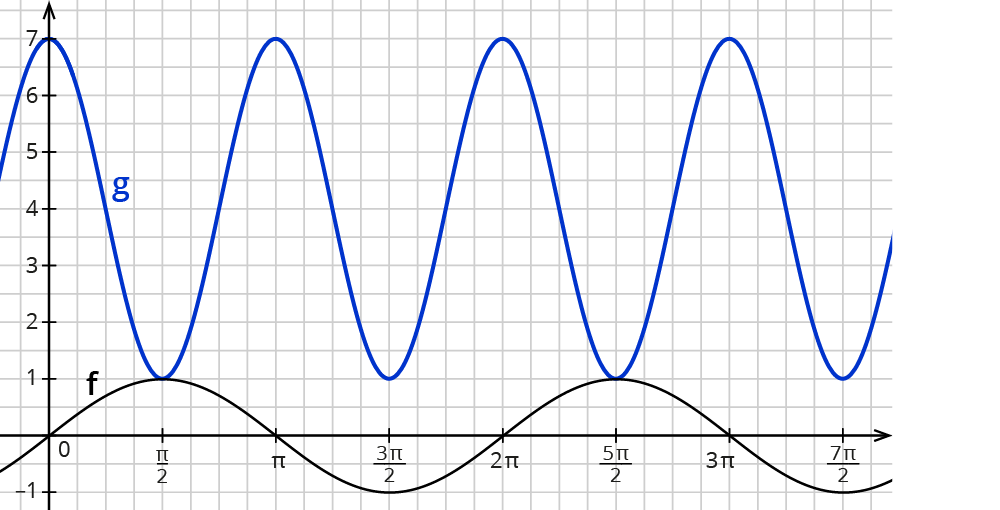
So sieht’s allgemein aus:
Der Graph der Funktion $$g(x)=a*sin(b*(x-c))+d$$ wird im Vergleich zu $$f(x)=sinx $$ durch die Parameter wie $$a,$$ $$b,$$ $$c,$$ $$d$$ so beeinflusst:
- $$a$$ staucht und streckt den Graphen in y-Richtung.
- $$b$$ staucht und streckt den Graphen in x-Richtung.
- $$c$$ verschiebt den Graphen in x-Richtung.
- $$d$$ verschiebt den Graphen in y-Richtung.
Für die Kosinusfunktion gilt wieder das Gleiche in Grün.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen