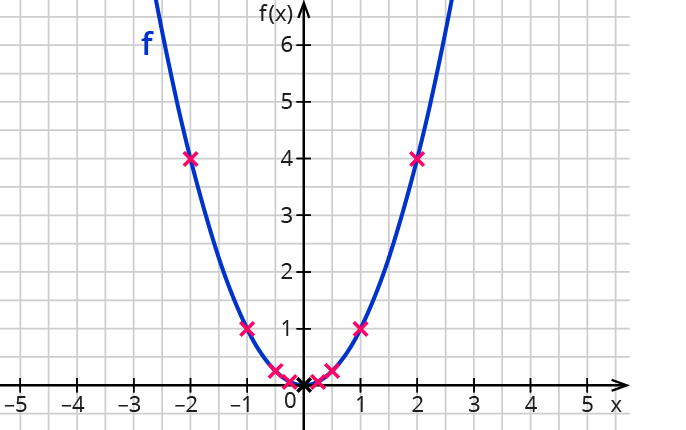
Eigenschaften quadratischer Funktionen bestimmen
Eigenschaften quadratischer Funktionen
Welche Eigenschaften haben all diese Funktionen?
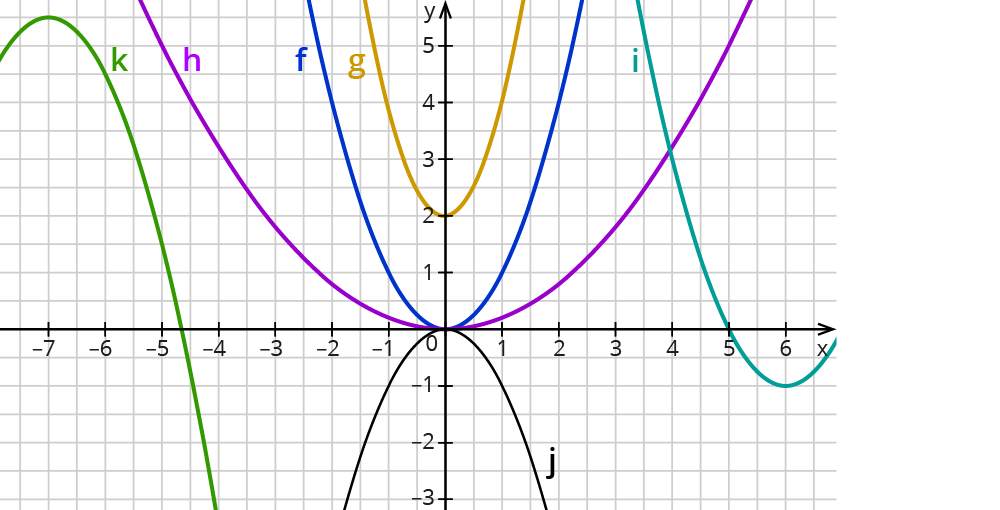
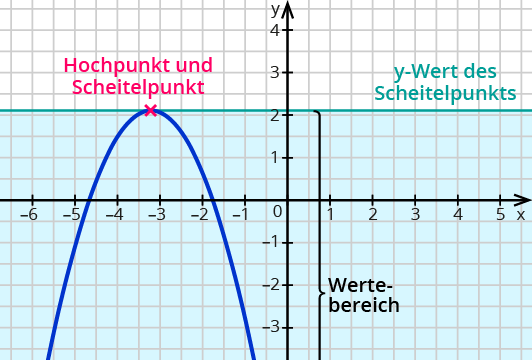
Hoch- oder Tiefpunkt, Scheitelpunkt
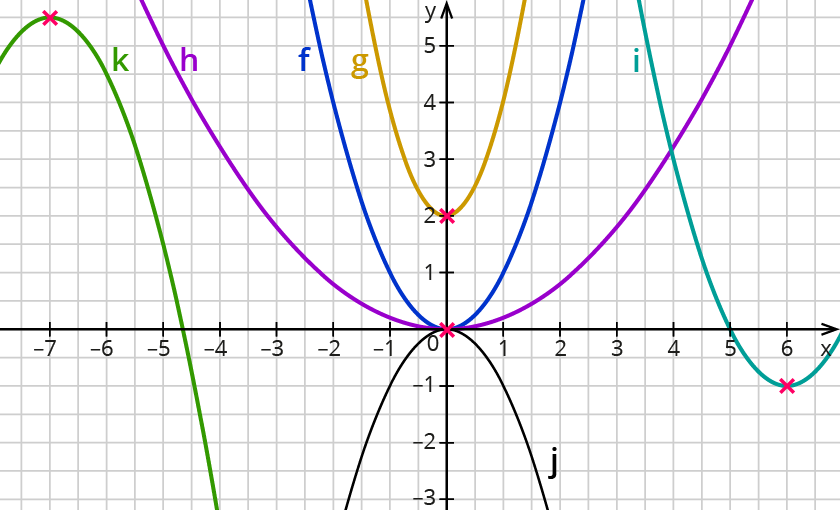
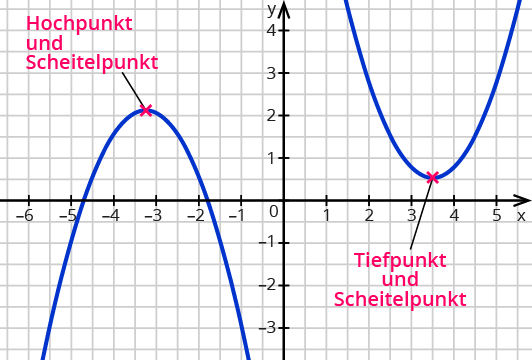
Bei allen abgebildeten Parabeln gibt es einen Punkt, der am höchsten oder am tiefsten ist.
Der höchste Punkt heißt Hochpunkt oder Maximum.
Der tiefste Punkt heißt Tiefpunkt oder Minimum.
Jede quadratische Funktion besitzt einen Hochpunkt oder einen Tiefpunkt.
Der Hoch- oder Tiefpunkt ist bei einer Parabel auch der Scheitelpunkt.
Zusammenfassung
Wertebereich
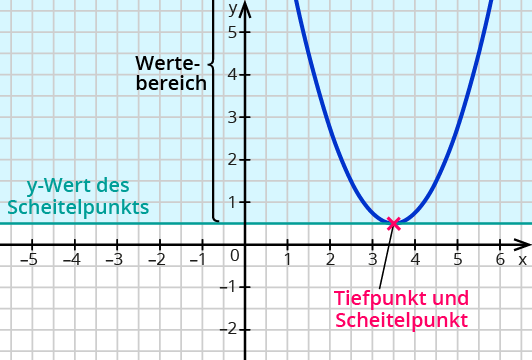
Den Wertebereich der Funktion kannst du sofort angeben, wenn du den Scheitelpunkt der Parabel kennst und weißt, ob es Tiefpunkt oder Hochpunkt ist.
1. Der Scheitelpunkt ist ein Tiefpunkt
Dafür ein Beispiel:
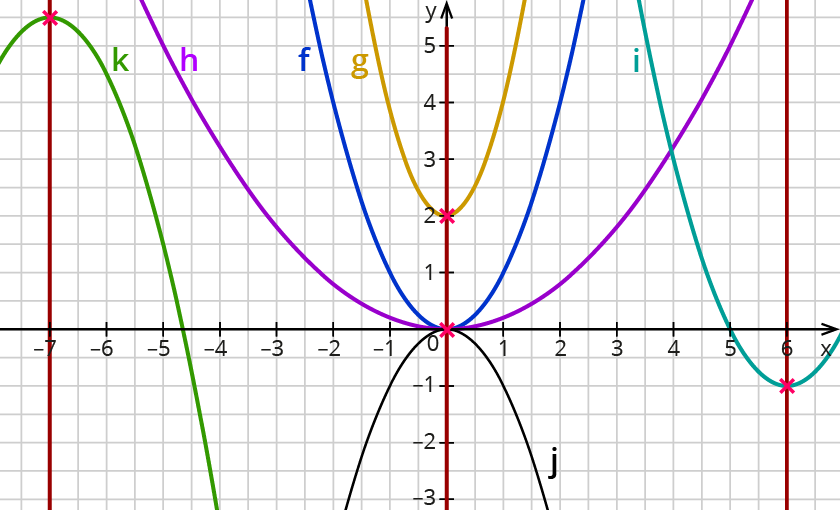
Der Scheitelpunkt der blauen Parabel liegt bei (6| - 1).
Welche Werte kann die Funktion annehmen?
Die Funktion nimmt nur Werte an, die -1 oder größer sind. -1 ist der $$y$$-Wert des Scheitelpunktes.
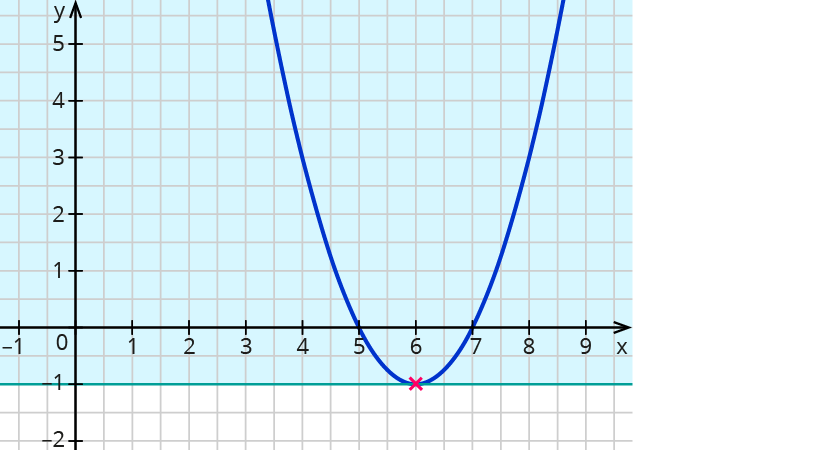
Mathematisch: Der Wertebereich der Funktion ist $$W={y in RR| y ≥ 1}$$.
Wenn der Scheitelpunkt ein Tiefpunkt ist, weißt du:
Die Funktion nimmt alle Werte an, die größer als und gleich dem $$y$$-Wert des Scheitelpunkts sind.
2. Der Scheitelpunkt ist ein Hochpunkt
Auch dafür ein Beispiel:
Der Scheitelpunkt der lila Parabel liegt bei (-7| 5,5).
Welche Werte kann diese Funktion annehmen?
Die Funktion nimmt nur Werte an, die 5,5 oder kleiner sind.
5,5 ist der $$y$$-Wert des Scheitelpunktes.
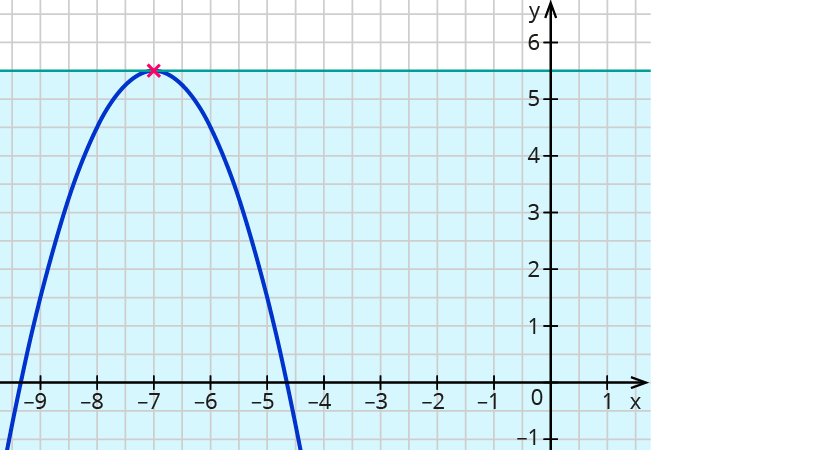
Mathematisch: Der Wertebereich der Funktion ist $$W={y in RR| y ≤ 5,5}$$.
Wenn der Scheitelpunkt ein Hochpunkt ist, weißt du:
Die Funktion nimmt alle Werte an, die kleiner als und gleich dem $$y$$-Wert des Scheitelpunkts sind.
Zusammenfassung
Zusammenfassung
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Symmetrie
Sind die Parabeln symmetrisch?
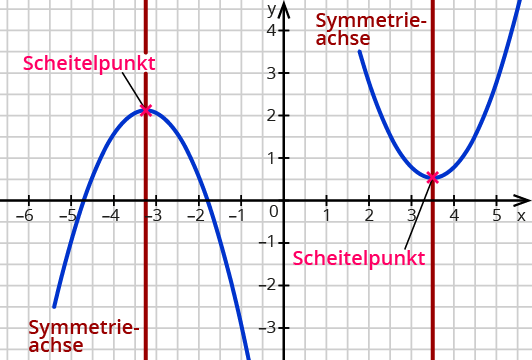
Wenn du durch den Scheitelpunkt eine Gerade legst, die parallel zur $$y$$-Achse verläuft, siehst du es. Zu dieser Geraden ist die Parabel symmetrisch.
Eine Parabel ist zur Geraden symmetrisch, die durch ihren Scheitelpunkt verläuft und zur $$y$$-Achse parallel ist.
Zusammenfassung
Nullstellen
Die Punkte, an denen ein Graph die $$x$$-Achse schneidet, heißen Nullstellen.
$$f(x)$$ ist hier $$0$$, also $$f(x)=0$$.
Wie viele Nullstellen kann eine Parabel besitzen?
Bei Parabeln kann es drei unterschiedliche Situationen geben.
1. Keine Nullstelle
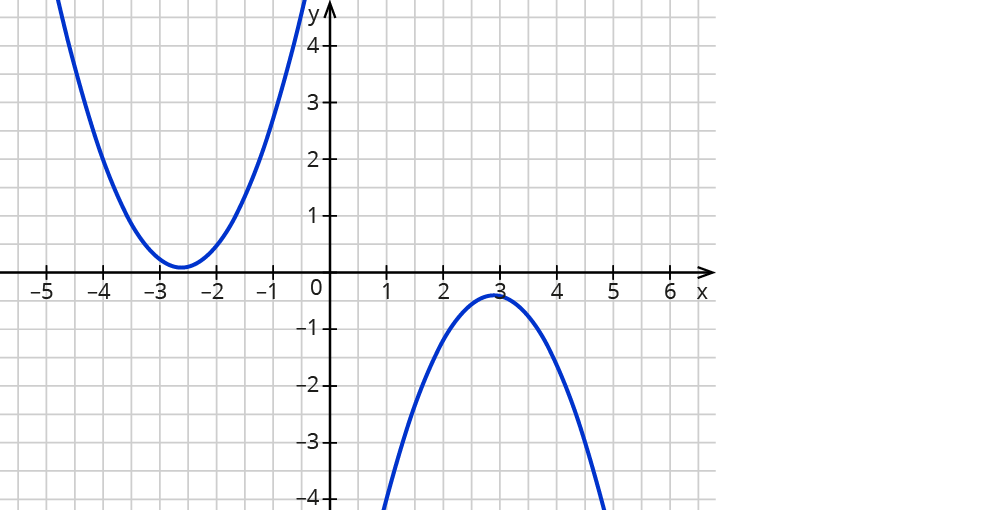
Liegt der Hochpunkt unter der $$x$$-Achse oder der Tiefpunkt über der $$x$$-Achse, schneidet die Parabel die $$x$$-Achse nicht.
2. Eine Nullstelle
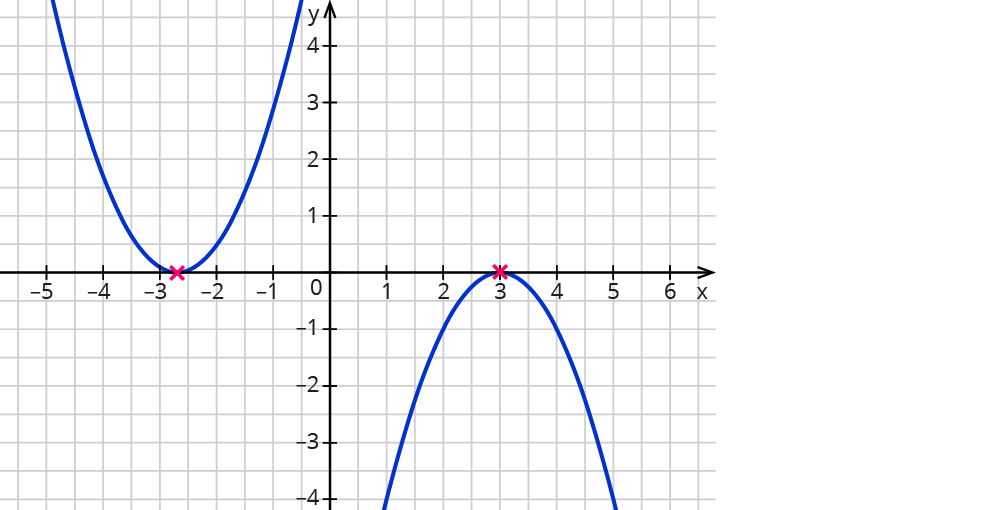Liegt der Scheitelpunkt auf der $$x$$-Achse, hat die Parabel genau eine Nullstelle.
3. Zwei Nullstellen
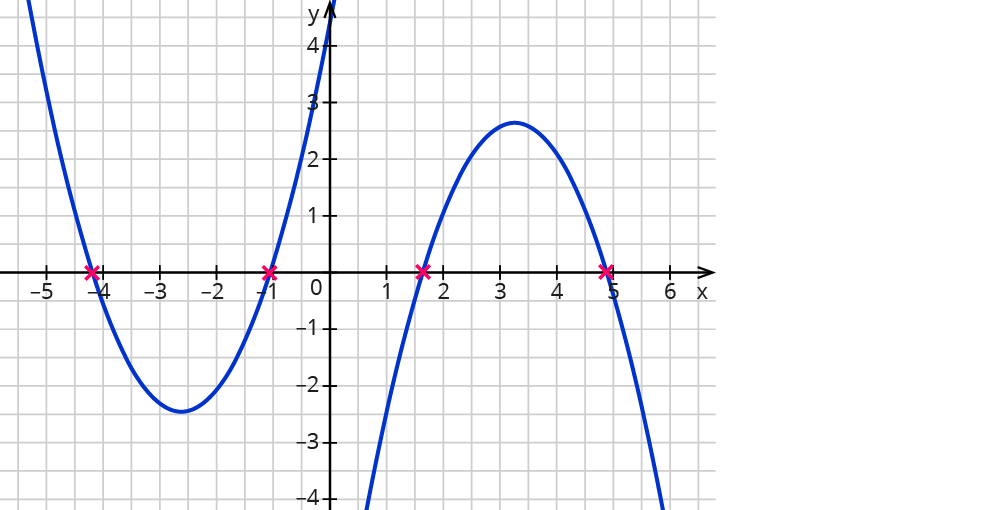Liegt der Hochpunkt über $$x$$-Achse oder der Tiefpunkt unter $$x$$-Achse, hat die Parabel zwei Nullstellen.
Quadratische Funktionen im Überblick
Was haben alle quadratischen Funktionen gemeinsam?
Quadratische Funktionen besitzen entweder einen Hochpunkt oder einen Tiefpunkt. Dieser Punkt ist auch der Scheitelpunkt.
Der Wertebereich setzt sich aus dem $$y$$-Wert des Scheitelpunkts zusammen und
– allen Werten oberhalb des Scheitelpunktes, wenn es ein Tiefpunkt ist.
– allen Werten unterhalb des Scheitelpunktes, wenn es ein Hochpunkt ist.Quadratische Funktionen besitzen eine Spiegelachse. Sie verläuft parallel zur $$y$$-Achse durch den Scheitelpunkt.
Quadratische Funktionen besitzen entweder keine, eine oder zwei Nullstellen.
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
