Anwendungsaufgaben mit Zufallsexperimenten
Zufall mit Mathe
Münze, Urne, Würfel, Kartenspiel - hier siehst du nochmal im Überblick, was du mit Zufallsexperimenten alles anstellen kannst.
Hieran erkennst du ein Zufallsexperiment:
- Das Experiment hat mindestens zwei eindeutige Ergebnisse, die du nicht vorhersagen kannst.
- Das Experiment kann unter gleichen Bedingungen beliebig oft wiederholt werden.
Ergebnisse aufschreiben
Alle Ergebnisse, die ein Zufallsexperiment haben kann, schreibst du in die Ergebnismenge.
Würfeln:
Ergebnismenge: { 1 ; 2 ; 3 ; 4 ; 5 ; 6 }
Münze werfen:
Ergebnismenge: { Kopf ; Zahl }

Bild: fotolia.com (p!xel 66)
Häufigkeiten
Die absolute Häufigkeit ist eine Anzahl. Damit wird gezählt, wie oft etwas vorkommt.
Die relative Häufigkeit ist der Anteil an einer Gesamtzahl. Du schreibst sie als Bruch oder Dezimalbruch.
Die relative Häufigkeit eines Ergebnisses ist der Quotient aus der absoluten Häufigkeit und der Gesamtzahl: $$relative \ Häufigkeit = frac{ab solute \ Häufigkeit}{Gesamtzahl}$$
Beispiel:
Du wirfst 100 mal eine Münze. Davon sind 57 Würfe Kopf und 43 Würfe Zahl.
| Ergebnis | absolute Häufigkeit | relative Häufigkeit |
|---|---|---|
| Kopf | 57 | $$57/100=0,57$$ |
| Zahl | 43 | $$43/100=0,43$$ |
Wahrscheinlichkeiten
Aber du kannst ja nun nicht für jedes Zufallsexperiment die Ergebnisse auszählen. Und eigentlich weißt du ja, wie wahrscheinlich Kopf oder Zahl ist.
Die Wahrscheinlichkeit eines Ergebnisses ist die erwartete relative Häufigkeit dieses Ergebnisses. Das Symbol ist $$p$$.
Beispiel Münze werfen:
Ergebnis Kopf: $$p=1/2$$
Ergebnis Zahl: $$p=1/2$$
Wenn bei einem Zufallsexperiment alle möglichen Ergebnisse mit gleicher Wahrscheinlichkeit auftreten, berechnest du die Wahrscheinlichkeit $$p$$ so:
$$p = frac{Anzahl \ der \ günsti g en \ Er g ebnisse}{Anzahl \ der \ möglichen \ Er g ebnisse}$$
Beispiel Spielkarten:
Mit welcher Wahrscheinlichkeit ziehst du eine Karte mit der Farbe „Herz“?

Ein Skatspiel besteht aus 32 Spielkarten. Es gibt 8 Karten der Farbe „Herz“.
Mögliche Ergebnisse: 32
Günstige Ergebnisse: 8
$$p = frac{8}{32}=1/4=0,25$$
Die Wahrscheinlichkeit, aus einem Skatspiel die Farbe „Herz“ zu ziehen, beträgt $$p = frac{1}{4}$$.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Baumdiagramme
Zufallsexperimente kannst du mehrmals hintereinander durchführen. Damit du nicht den Überblick verlierst, zeichnest du dir ein Baumdiagramm.
Beispiel:
Zu ziehst zweimal aus dieser Urne und legst die Kugeln immer zurück.
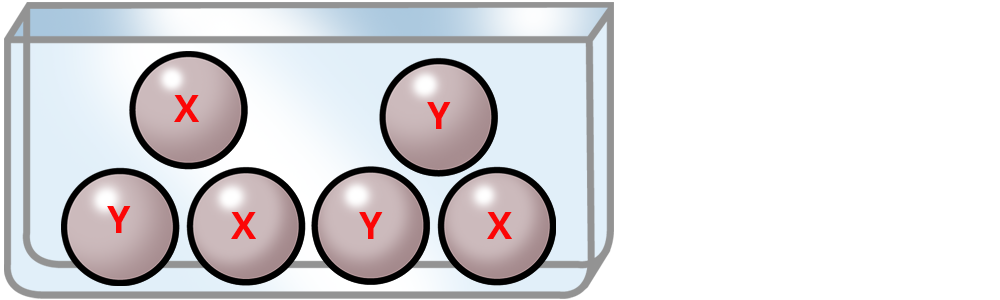
Die Wahrscheinlichkeit X zu ziehen: $$3/6=1/2$$
Die Wahrscheinlichkeit Y zu ziehen: $$3/6=1/2$$
Das Baumdiagramm:
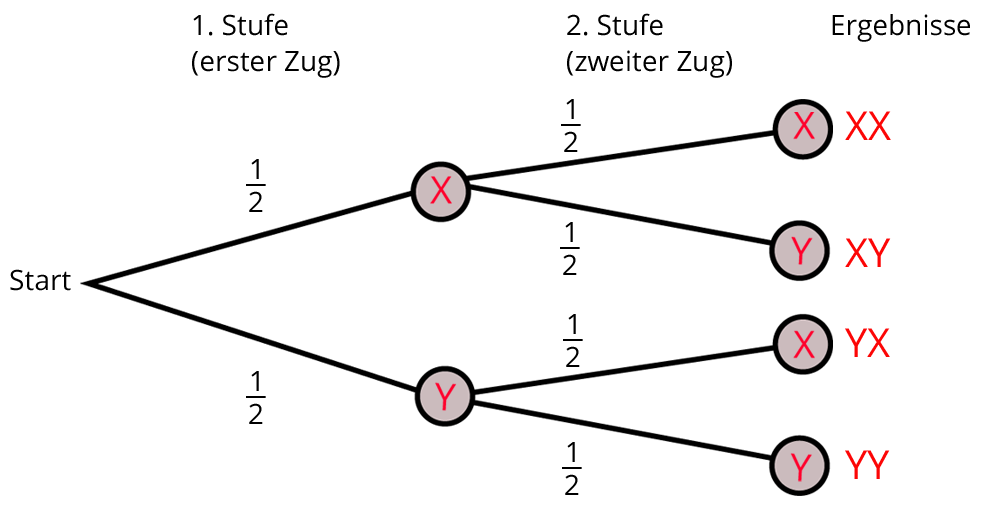
Die Ergebnismenge ist: { XX ; YX ; XY ; YY }
Wie groß ist die Wahrscheinlichkeit, zweimal hintereinander X zu ziehen?
Die Wahrscheinlichkeit, beim ersten Ziehen „X“ zu erhalten, ist $$1/2$$. Die Wahrscheinlichkeit, beim zweiten Ziehen „X“ zu erhalten, ist $$1/2$$. Multipliziere:
$$p=1/2*1/2=1/4$$
Oder:
Du überlegst dir, dass alle Ergebnisse gleichwahrscheinlich sind und rechnest so:
Mögliche Ergebnisse: 4 $$rarr$$ „XX“, „YX“, „XY“, „YY“
Günstige Ergebnisse: 1 $$rarr$$ „XX“
Die Wahrscheinlichkeit für „XX“ ist $$p =frac{1}{4}$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



