Dreisatz: Antiproportionale Zuordnungen
Der Dreisatz bei antiproportionalen Zuordnungen
Beispiel: Ein Schwimmbecken wird von 4 gleichgroßen Rohren in 100 Minuten gefüllt. Wie lange würde es dauern, wenn 5 Rohre eingesetzt werden?

Du weißt nicht, wie du vorgehen sollst?
Das ist der Trick:
Du baust einen Zwischenschritt ein. Das heißt, du überlegst dir eine Zahl, auf die du
- leicht runterrechnen kannst und
- leicht auf den gesuchten Wert hochrechnen kannst.
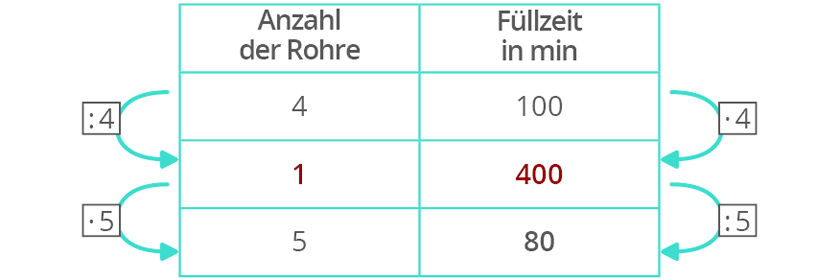
Vielleicht siehst du an der Tabelle, warum diese Aufgaben Dreisatz heißen. Du rechnest in 3 Sätzen (in 3 Schritten).


Den Zwischenschritt wählen
Der Zwischenschritt muss nicht immer die 1 sein (Jedoch passt die 1 immer).
Beispiel: 30 Bauarbeiter benötigen für eine neue Straße 10 Tage. Wie lange brauchen 20 Bauarbeiter?
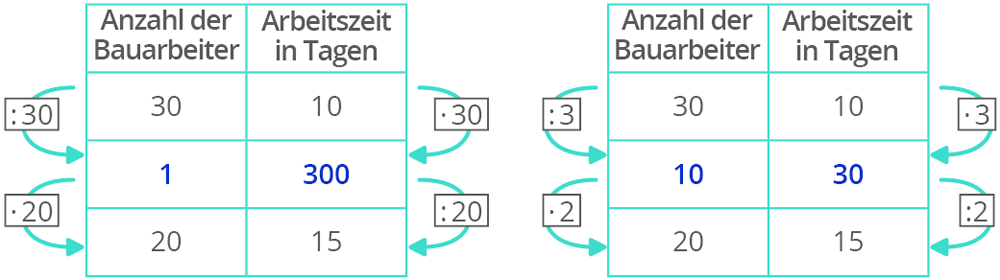
Du kannst die 1 als Zwischenschritt wählen. Aber mit 10 als Zwischenschritt kannst du viel leichter rechnen.
- Tabelle erstellen und Werte aus dem Text eintragen
- Möglichst größten gemeinsamen Teiler als Zwischenschritt finden
(Die 1 geht immer) - Gesuchten Wert berechnen
Schwierige Textaufgaben lösen
Beispiel: 13 Maler haben in einer Neubausiedlung 30 Tage Arbeit. Nach 8 Tagen werden 2 Maler krank. Wie viele Tage wird die Arbeit nun insgesamt dauern?
So geht’s:
Überlege dir zuerst, wie groß die zugeordnete Größe (hier Tage) ist.
Die 8 Tage, die bereits um sind, brauchst du nicht zu betrachten.
Rechne also mit $$30-8=22$$ Tagen weiter.
Wie lange müssen die verbleibenden 11 Maler arbeiten?
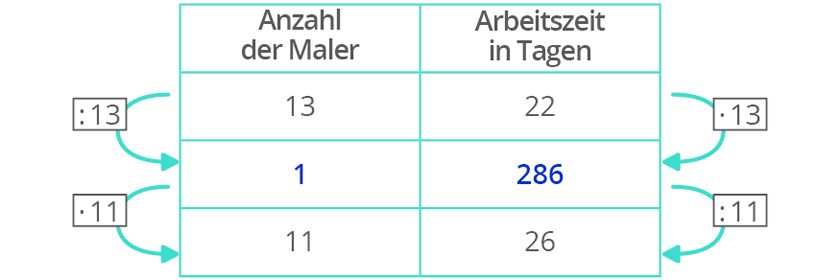
Wie lange arbeiteten die Maler insgesamt?
Addiere die bereits gearbeiteten Tage. $$26+8=34$$
Antwort: Insgesamt benötigen die Arbeiter 34 Tage.
 Bild: Druwe & Polastri
Bild: Druwe & Polastri

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Das Kurzschema beim Dreisatz
Beispiel:3 Pflasterer brauchen 12 Stunden, um eine Einfahrt zu pflastern. Wie lange brauchen 4 Pflasterer?
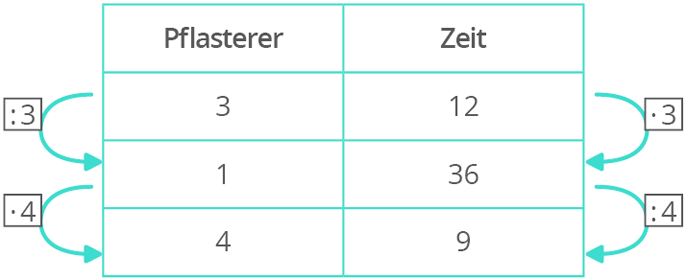
Das Kurzschema funktioniert immer. Du kannst es auch ohne Tabelle benutzen.
3 Pflasterer $$->$$ 12 Stunden
1 Pflasterer $$->$$ 3 mal so lange
4 Pflasterer $$->$$ ein Viertel der Zeit
Also rechnest du: (12 $$*$$ 3) $$:$$ 4 = 9
Oder: 
Das Kurzschema ohne Tabelle
Beispiel: Ein Gartenbeet soll mit kleinen Pflanzen eingefasst werden. Setzt du sie 10 cm auseinander, dann brauchst du 500 Stück. Wie viele Pflanzen brauchst du bei einem Abstand von 8 cm?
10 cm $$->$$ 500 Pflanzen
1 cm $$->$$ 10 mal so viel
8 cm $$->$$ ein Achtel der Pflanzen
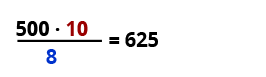
Einen einfachen Dreisatz berechnest du ohne Tabelle:
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



