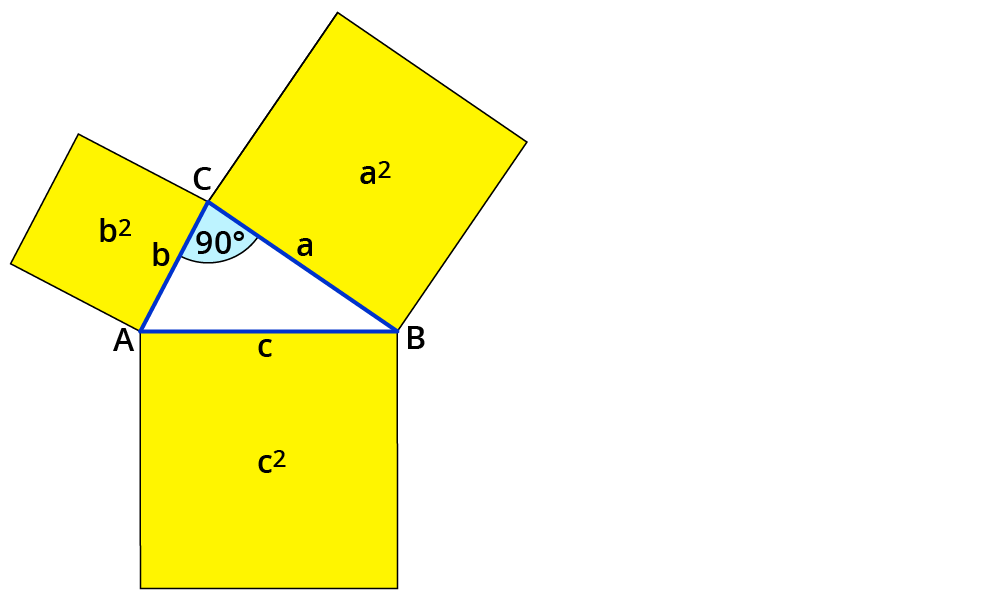
Geometrische Beweise durchführen
Mathe ist mehr als Rechnen
Die hohe Kunst in der Mathematik ist das schlüssige Argumentieren. Dabei musst du gar nichts rechnen, sondern beschäftigst dich mit mathematischen Theorien.
Mathematische Theorien bestehen aus Aussagen, die man meistens mit anderen bekannten Aussagen begründen können muss. Der Mathematiker sagt dazu beweisen. Jedoch muss es für eine solche Theorie einen unbeweisbaren Anfang geben.
Der „Anfang“ einer solchen Theorie besteht aus den sogenannten Axiomen. Axiome sind offensichtlich wahre und logische Grundsätze, die niemand bestreiten würde.
Beispiel für ein Axiom aus der Geometrie: Drei nicht auf ein und derselben Geraden liegende Punkte $$A$$, $$B$$, $$C$$ bestimmen stets eine Ebene.
Aufbau einer mathematischen Theorie
Aus den Axiomen formulierst du dann Definitionen.
Ein Beispiel aus der Geometrie: Zwei Geraden heißen parallel, wenn sie entweder identisch sind oder in einer Ebene liegen und keinen gemeinsamen Punkt haben.
Schließlich stellst du auf der Grundlage von Definitionen eine Behauptung auf, die du aus anderen Behauptungen oder Definitionen beweisen können musst. Dafür wirst du in dieser Einheit zahlreiche Beispiele finden.
Zusammenfassung:
Axiome
$$darr$$
Definitionen
$$darr$$
Behauptungen
$$darr$$
Beweise
Struktur eines mathematischen Beweises
Der mathematische Beweis dient dir dazu, eine Behauptung für wahr oder falsch zu erklären.
Dazu verwendest du sogenannte Beweismittel. Das sind Axiome, Definitionen oder bereits bewiesene mathematische Aussagen.
Zu Beginn formulierst du Voraussetzungen, auf die sich der Beweis stützen soll.
Den Beweis schließt du mit „q.e.d.“ („quod erat demonstrandum“ oder „was zu beweisen war“) ab.
Beispiel aus der Zahlentheorie
Beweise, dass das Quadrat einer geraden Zahl wieder gerade ist.
Voraussetzung: $$n$$ sei eine gerade Zahl, es gilt also $$n=2k$$ mit $$k, n in IN$$.
Behauptung: Dann ist $$n^2$$ auch gerade.
Beweis: $$n^2 stackrel(Vo\raussetzung)= (2k)^2=4k^2= 2*2k^2$$
└─┬─┘
wieder gerade
Also ist $$2$$ ein Teiler von $$n^2$$ und $$n^2$$ damit gerade. q.e.d.Beispiel aus der Satzgruppe des Pythagoras
Beweis des Höhensatzes
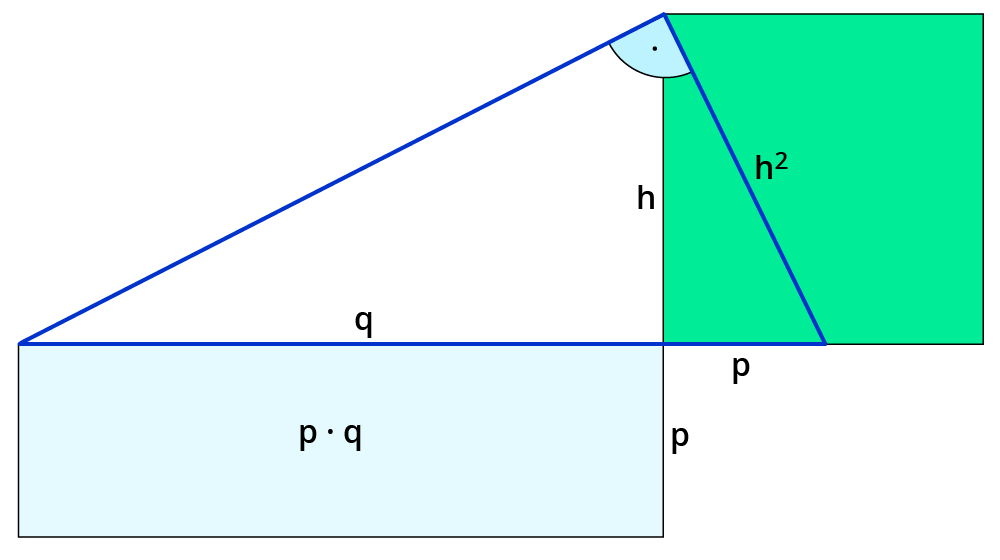
Der Höhensatz besagt: $$h^2=p*q$$
Beweise den Höhensatz unter Verwendung des Satzes des Pythagoras.
Voraussetzung: Gegeben sei ein rechtwinkliges Dreieck ABC mit $$gamma=90$$° wie unten in der Abbildung. Es gilt der Satz Pythagoras: $$a^2+b^2=c^2$$. Außerdem gilt $$c=p+q$$.
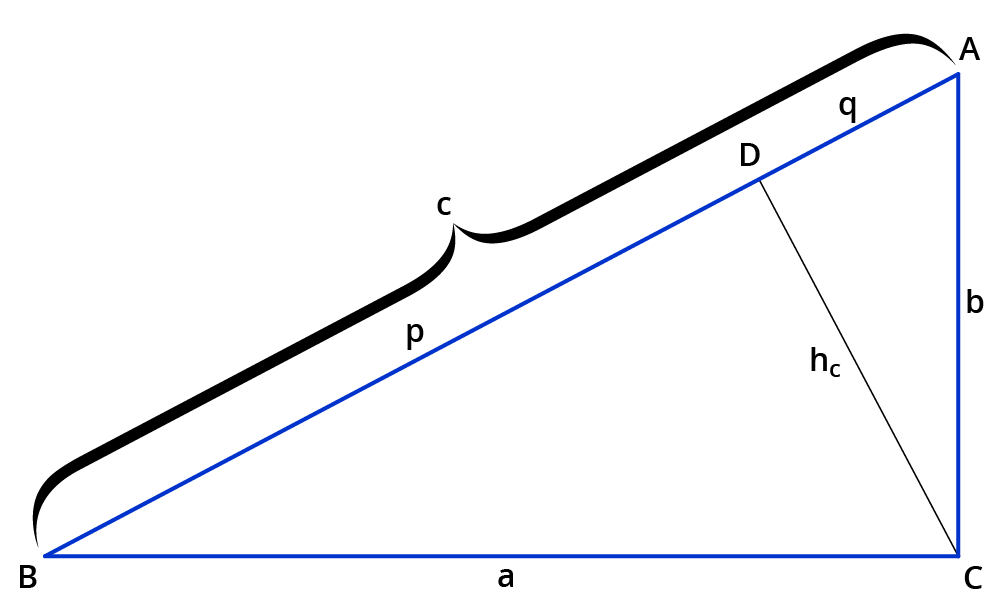
Der Satz des Pythagoras gilt auch im Dreieck $$ADC$$: $$b^2=h_c^2+q^2$$.
Der Satz des Pythagoras gilt auch im Dreieck $$DBC$$: $$a^2=h_c^2+p^2$$.
Behauptung: Im Dreieck $$ABC$$ gilt Höhensatz: $$h_c^2=p*q$$
Beweis:
$$c^2=a^2+b^2$$
$$hArr (p+q)^2=(h_c^2+p^2)+(h_c^2+q^2)$$
└─┬─┘
Binomische Formel
$$hArr p^2+2pq+q^2=h_c^2+p^2+h_c^2+q^2$$ $$|-p^2-q^2$$
$$hArr 2pq = 2h_c^2$$ $$|:2$$
$$hArr pq=h_c^2$$ q.e.d.
Beweise durch Widerspruch
Bei Beweisen durch Widerspruch nimmst du das Gegenteil der zu zeigenden Aussage an und führst dieses Gegenteil zu einem offensichtlichen Widerspruch.
Im Umkehrschluss darfst du dann daraus folgern, dass die ursprüngliche Aussage gilt.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen