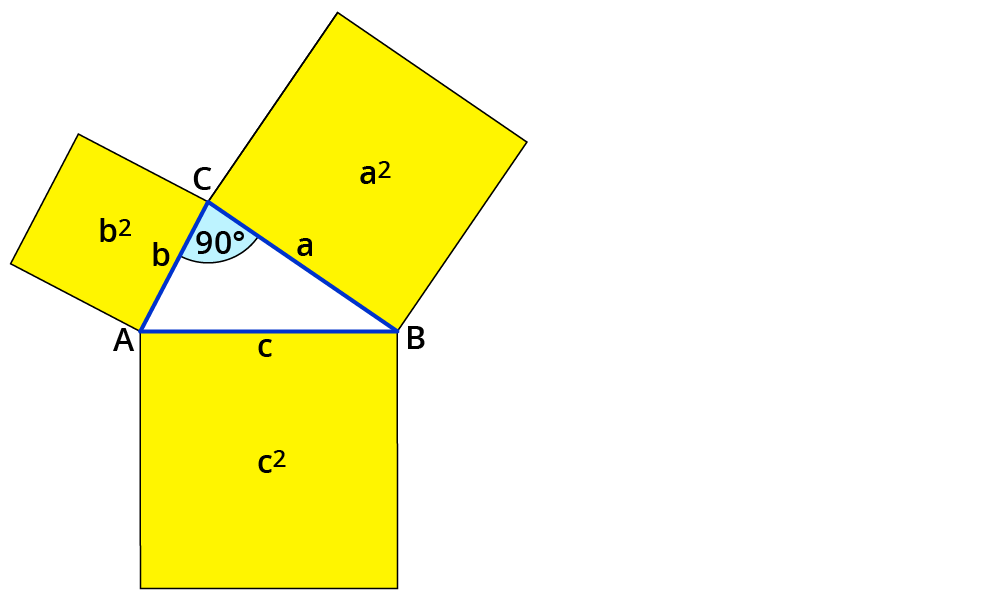
Den Satz des Thales anwenden
Der Satz des Thales
Der Satz des Thales wurde nach dem griechischen Philosophen und Mathematiker Thales von Milet (ca. 625 bis 545 v. Chr.) benannt.
Der Satz besagt:
Liegt der Punkt $$C$$ auf einem Kreis mit der Strecke $$bar (AB)$$ als Durchmesser, dann hat das Dreieck $$ABC$$ bei Punkt $$C$$ einen 90°-Winkel. Liegt $$C$$ nicht auf diesem Kreis, dann gibt es bei $$C$$ auch keinen 90°-Winkel.
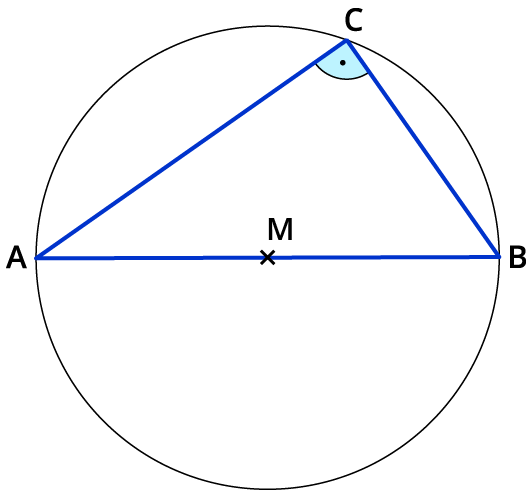
Beweis zum Satz des Thales
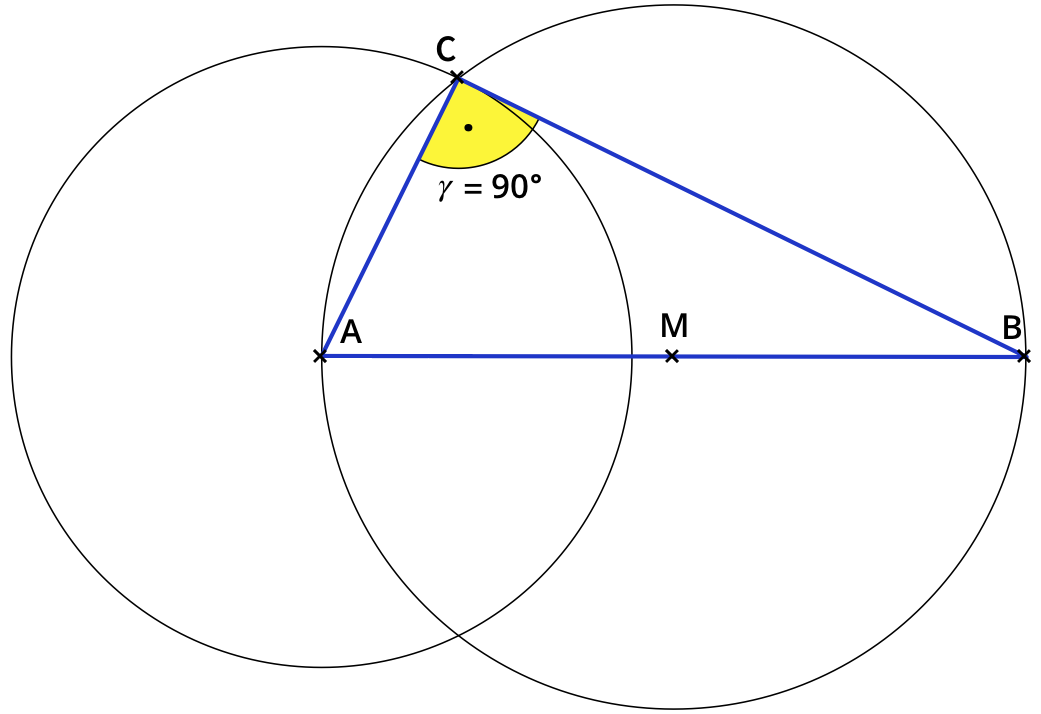
Wir wissen: Punkt $$C$$ liegt auf dem Halbkreis über $$bar (AB)$$.
Zu zeigen: $$γ = 90°$$
Beweis:
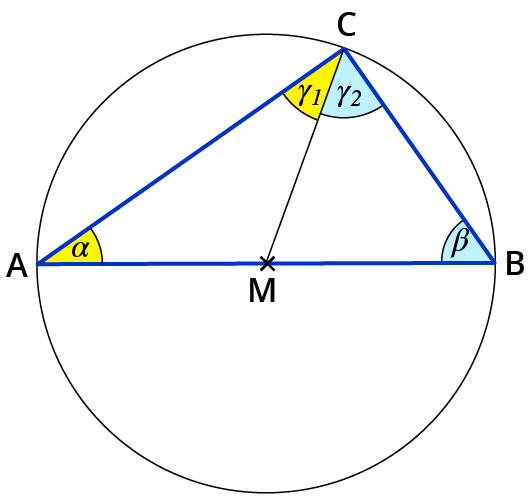
- Die Strecken $$bar (MA), bar (MB), bar (MC)$$ sind Radien des Kreises und damit alle gleich lang.
- Damit sind die Dreiecke AMC und AMB gleichschenklig und nach dem Basiswinkelsatz gilt: $$α=γ_1, β=γ_2$$.
- Also folgt: $$γ=γ_1 + γ_2 = α+β$$
- Mit dem Innenwinkelsummensatz im Dreieck folgt:
$$180°=α+β +γ=γ_1 + γ_2+γ=2γ$$ $$hArr$$ $$γ=90°$$ .
Wozu brauchst du den Satz des Thales?
1. Argumentieren
Zum einen kannst du leicht Aussagen über die Strecken $$bar (MA), bar (MB), bar (MC)$$ treffen. Sie sind Radien des Kreises und damit alle gleich lang.
Außerdem sind sie damit genau halb so lang wie die Strecke $$bar (AB)$$, da $$bar (AB)$$ der Durchmesser des Kreises ist. Es gilt: Das Doppelte vom Radius entspricht dem Durchmesser.

Wozu brauchst du den Satz des Thales?
2. Rechtwinklige Dreiecke konstruieren
Mit dem Satz des Thales kannst du rechtwinklige Dreiecke konstruieren. Der Punkt mit dem 90°-Winkel muss ja auf der Kreislinie liegen.
Konstruiere das Dreieck ABC mit:
$$c= bar (AB) =9cm$$, $$b= bar (AC) =4cm$$ und $$γ=90°$$.
So geht‘s:
Zeichne Seite $$c$$ und beschrifte die Enden mit $$A$$ und $$B$$.
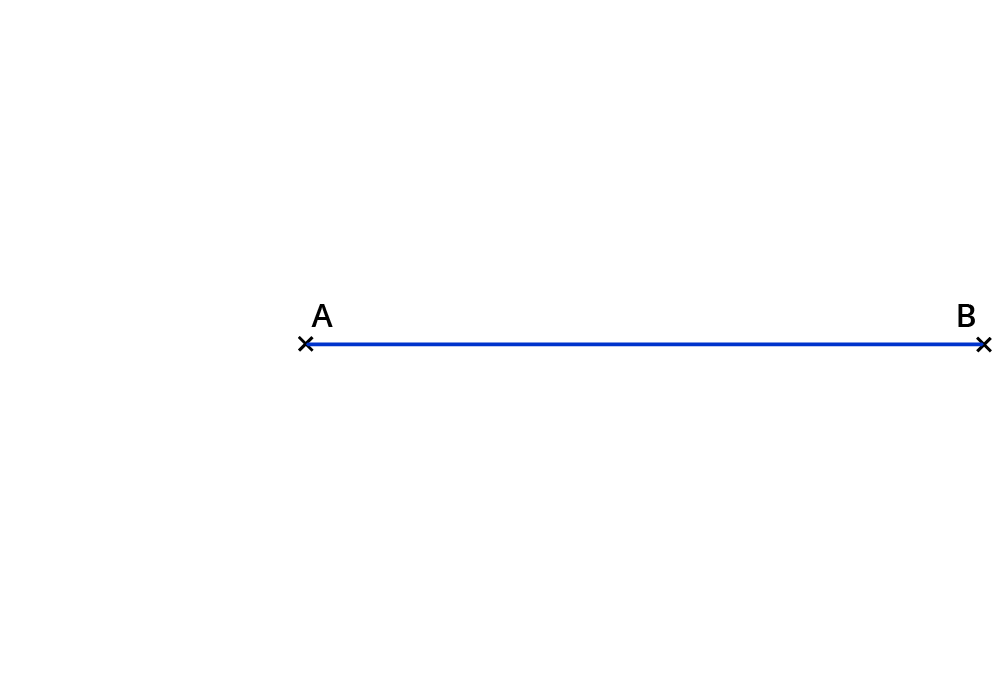
Konstruiere den Mittelpunkt $$M$$ von $$c$$.
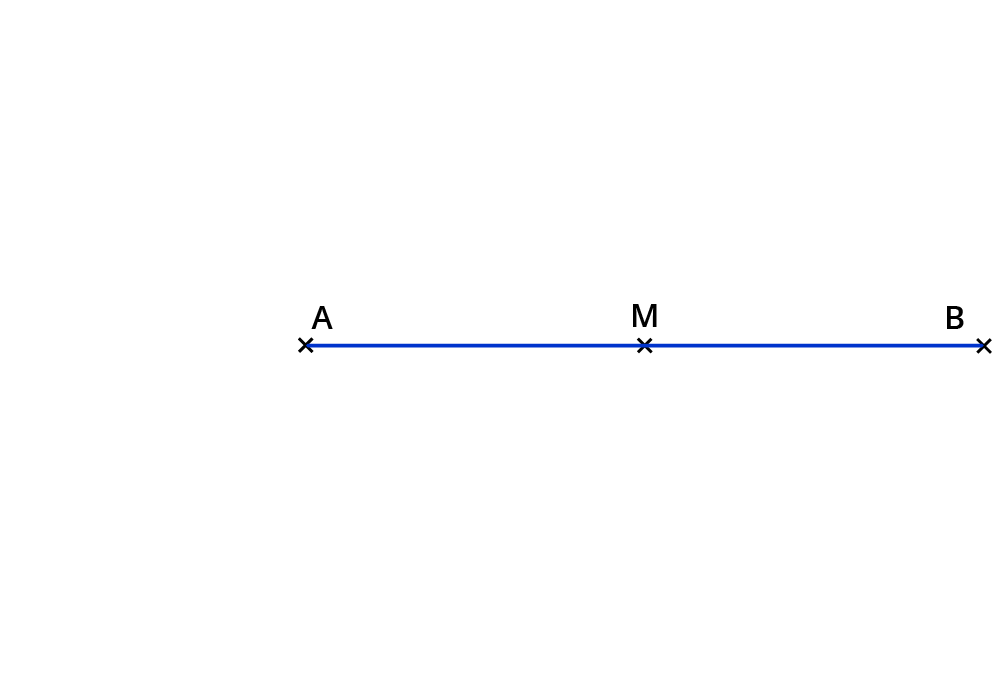
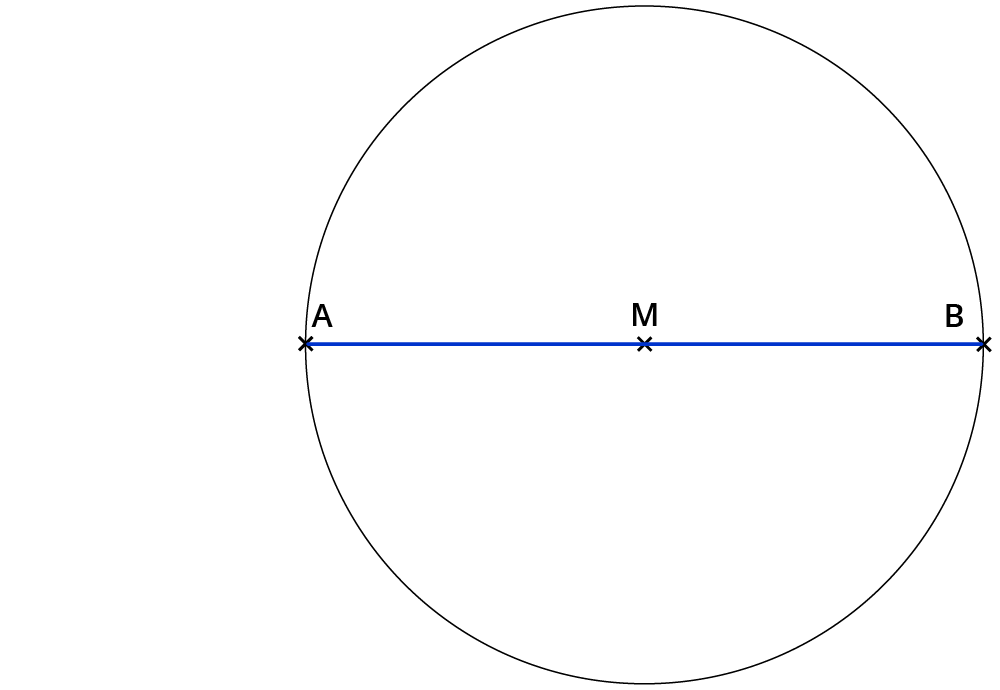
Zeichne um $$M$$ einen Kreis mit dem Durchmesser $$bar (AB)=9cm$$.
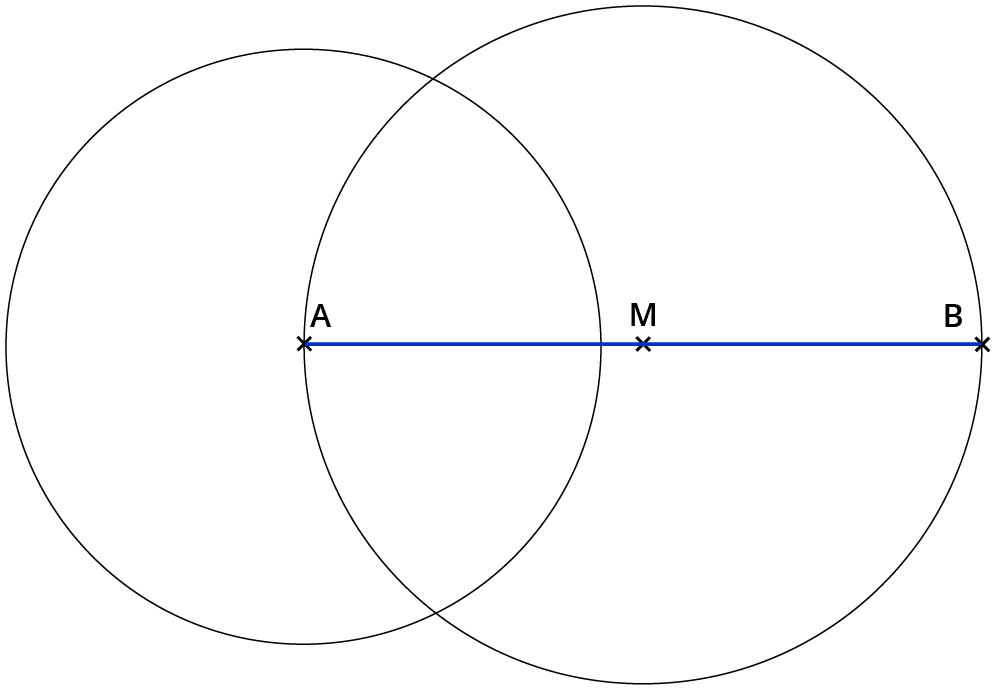
Ziehe um A einen Kreisbogen mit der Zirkelspanne $$4 cm$$.
Der Schnittpunkt beider Kreise ist der Punkt $$C$$.
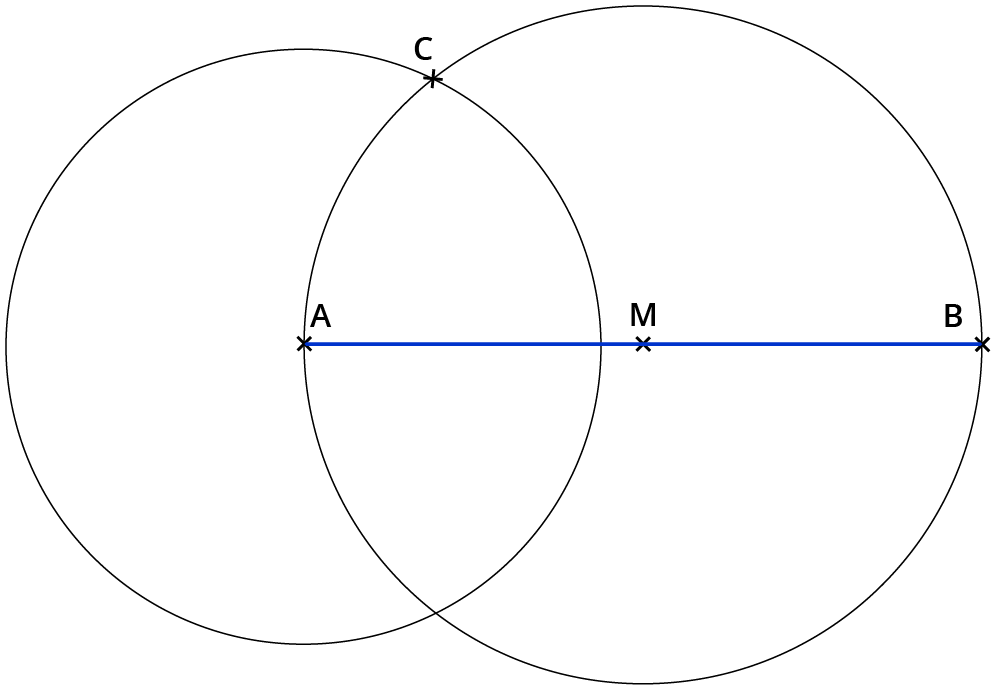
Verbinde die Punkte $$A$$, $$B$$ und $$C$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen