Den Satz des Pythagoras anwenden
Der Satz des Pythagoras in Worten
Mit dem Satz des Pythagoras kannst du Aussagen bezüglich der Seitenlängen und der Quadrate über den Seiten rechtwinkliger Dreiecke treffen.
Begriffe in rechtwinkligen Dreiecken:
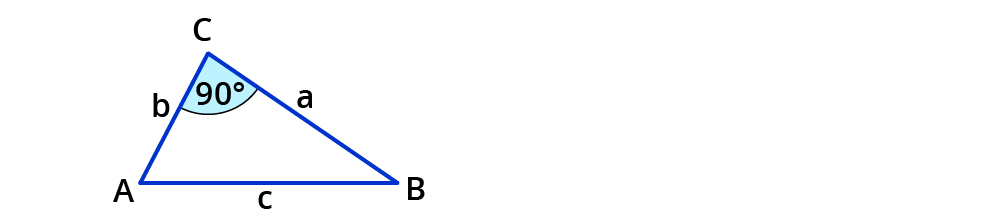Die Hypotenuse ist die längste Seite des Dreiecks, sie liegt dem 90°-Winkel gegenüber.
Die Katheten sind die kürzeren Seiten, die nicht dem 90°-Winkel gegenüber liegen.
Der Satz des Pythagoras besagt:
Satz des Pythagoras
In rechtwinkligen Dreiecken ist die Summe der Flächen der Quadrate über den Katheten genauso groß wie die Fläche des Quadrates über der Hypotenuse.
Der Satz des Pythagoras mit Variablen
So lässt sich der Satz des Pythagoras mit Variablen beschreiben:
Liegt der 90°-Winkel bei C, dann gilt: c2=a2+b2.
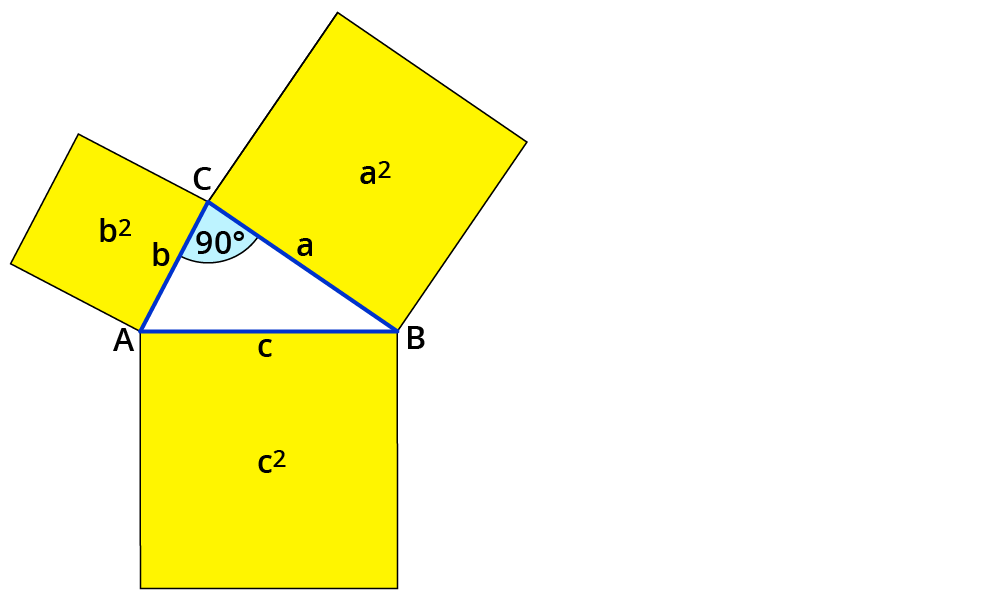
Liegt der 90°-Winkel bei B, dann gilt: b2=a2+c2.
Liegt der 90°-Winkel bei A, dann gilt: a2=c2+b2.
Mit dem Pythagoras rechnen
Der Satz eignet sich zum Berechnen von Seitenlängen.
Beispiel:
Berechne mit dem Satz des Pythagoras die Länger der Seite c.
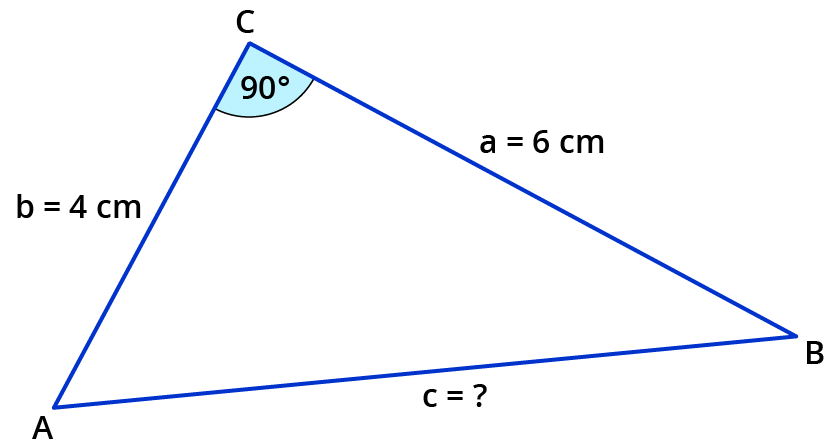
So gehst du vor:
1. Darfst du den Satz verwenden?
Ja, das Dreieck hat einen 90°-Winkel.
2. Wo liegt der rechte Winkel? Welche Formel nimmst du?
Der 90°-Winkel liegt bei C. Dann heißt die Formel: c2=a2+b2
3. Setze die Zahlen ein.
c2=(6 cm)2+(4 cm)2
4. Stelle die Gleichung nach der gesuchten Größe um und berechne.
c2=(6 cm)2+(4 cm)2=52 cm2 ∣ Wurzel ziehen
c=√52cm2≈7,2 cm
Oder erst umstellen und dann Zahlen einsetzen:
c2=a2+b2 ∣ Wurzel ziehen
c=√a2+b2=√(6cm)2+(4cm)2≈7,2 cm
Du kannst auch erst die Formel umstellen und dann die Zahlen einsetzen.
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Anwendung in Dreiecken mit anderen Bezeichnungen
Manchmal sind die Dreiecke nicht mit den Buchstaben a, b, c bezeichnet. Dann suchst du die Hypotenuse und formulierst danach die Gleichung.
Beispiel 1:
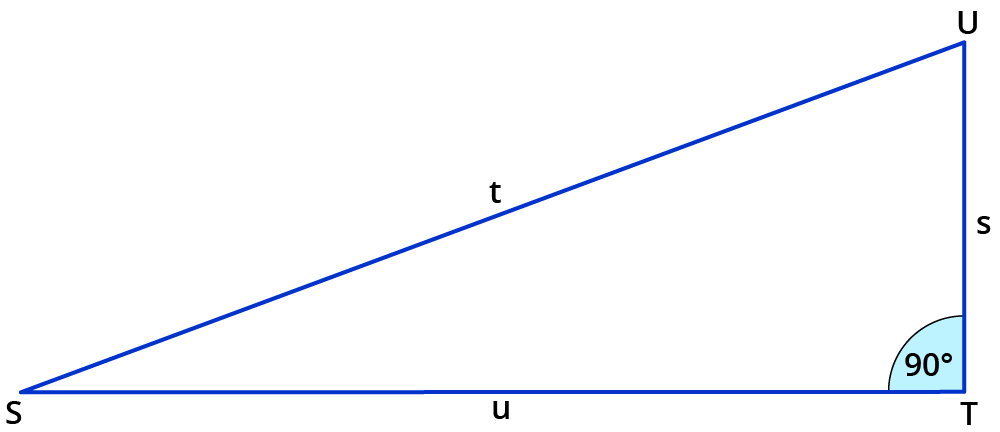
Der 90°-Winkel liegt t gegenüber, t ist also die Hypotenuse. Die Gleichung lautet t2=s2+u2.
Beispiel 2:
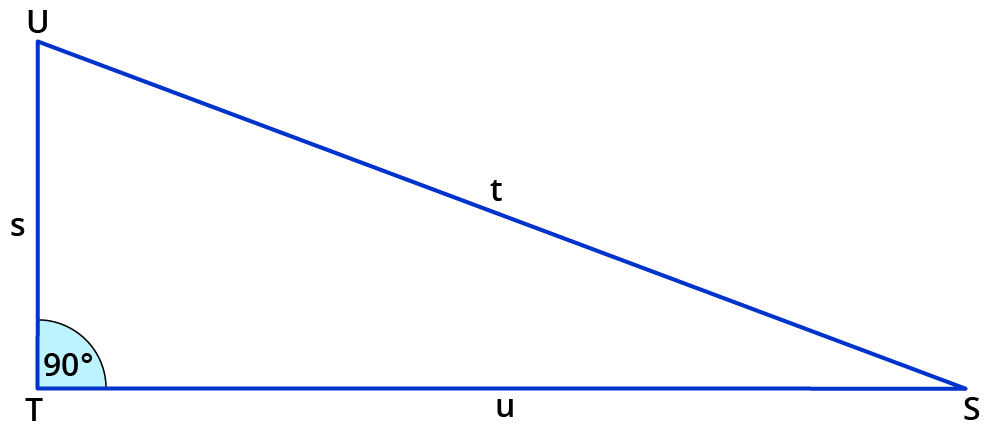
Der 90°-Winkel liegt t gegenüber, t ist also die Hypotenuse. Die Gleichung lautet t2=s2+u2. Dann formst du die Gleichungen nach der gesuchten Größe um.
Rechenbeispiel
Es wurde im Abstand von 250 m von einem Turm ein 255 m-langes Seil gespannt. Wie hoch ist der Turm?
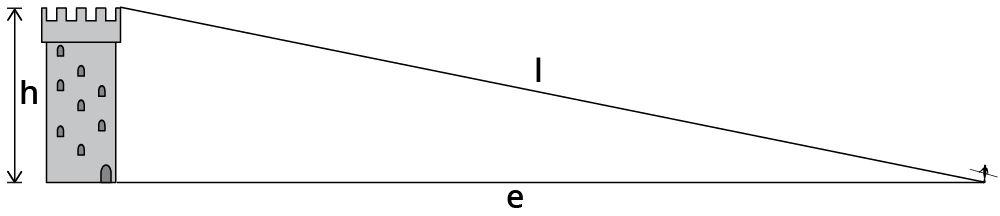
1. Darfst du den Satz verwenden?
Ja, der Turm steht ja senkrecht auf der Erde.
2. Wo liegt der rechte Winkel? Welche Formel nimmst du?
h und e schließen einen rechten Winkel ein.
Dann heißt die Formel: l2=e2+h2
e=250 m, l=255 m, l ist die Hypotenuse.
Gesucht ist h.
3. Setze die Zahlen ein.
(255 m)2=(250 m)2+ h2
4. Stelle die Gleichung nach der gesuchten Größe um und berechne.
(255 m)2=(250 m)2+ h2 ∣-(250 m)2
(255 m)2-(250 m)2=2525 m2= h2 ∣√
h=√2525m2≈50,25 m
Der Turm ist 50,25 m hoch.
Oder erst umstellen und dann Zahlen einsetzen:
l2=e2+h2 ∣-e2 dann ∣√
h=√l2-e2=√(255m)2-(250m)2
h≈50,25 m
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
