Winkelbeziehungen am Einheitskreis
Viele Winkel - ein Sinuswert
Der Sinus von 30° ist 0,5. Wenn du weiter um den Einheitskreis wanderst, siehst du, dass auch der Sinus von 150° gleich 0,5 ist.
$$sin(30^°)=sin(150^°)=0,5$$
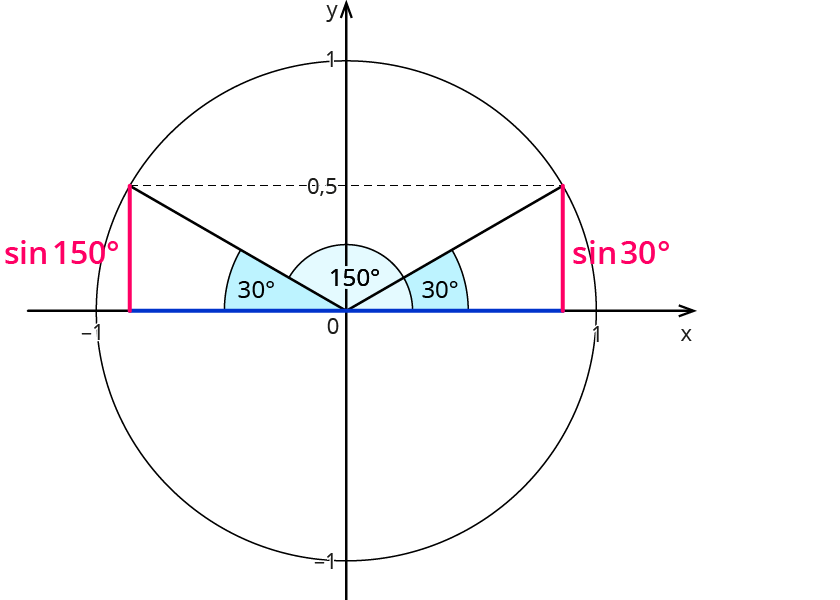
Wie ist der Zusammenhang zwischen verschiedenen Winkeln und gleichen Sinuswerten genau?
Das rechte Dreieck ist gespiegelt an der y-Achse.
Der 150°-Winkel ergibt sich aus $$180^°-30^°$$ oder allgemein $$180^°-alpha$$.
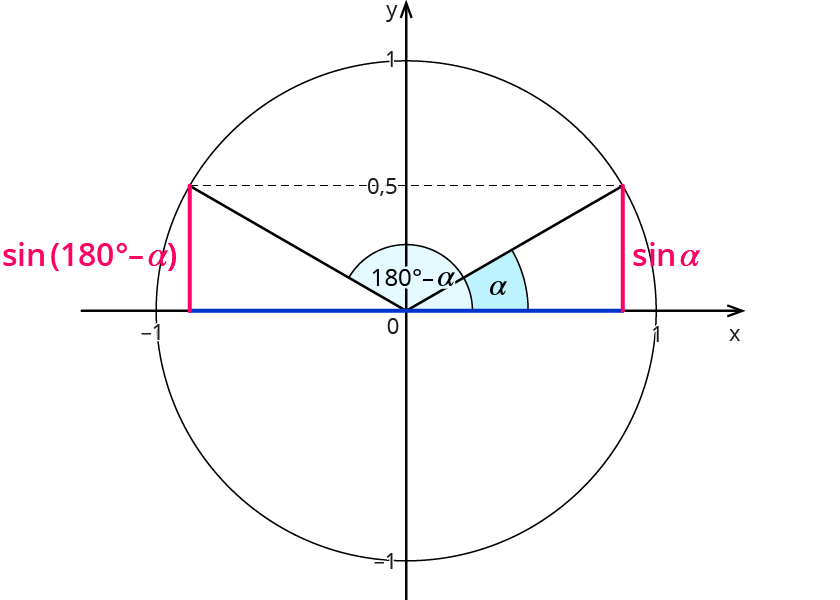
| Gradmaß | Bogenmaß |
| $$sin(alpha)=sin(180^°-alpha)$$ | $$sin(x)=sin(pi-x)$$ |
Zur Erinnerung:
$$pi$$ im Bogenmaß entspricht 180° im Gradmaß.
Noch mehr Beziehungen
Wenn du weiterwanderst auf dem Einheitskreis, ergeben sich noch mehr Beziehungen.
Beispiel:
$$sin(30^°)=0,5$$ und $$sin(210^°)=-0,5$$.

Allgemein gilt:
| Gradmaß | Bogenmaß |
| $$sin(alpha)=-sin(180^°+alpha)$$ | $$sin(x)=-sin(pi+x)$$ |
Und diese Beziehung hier:
Beispiel:
$$sin(30^°)=0,5$$ und $$sin(330^°)=-0,5$$.
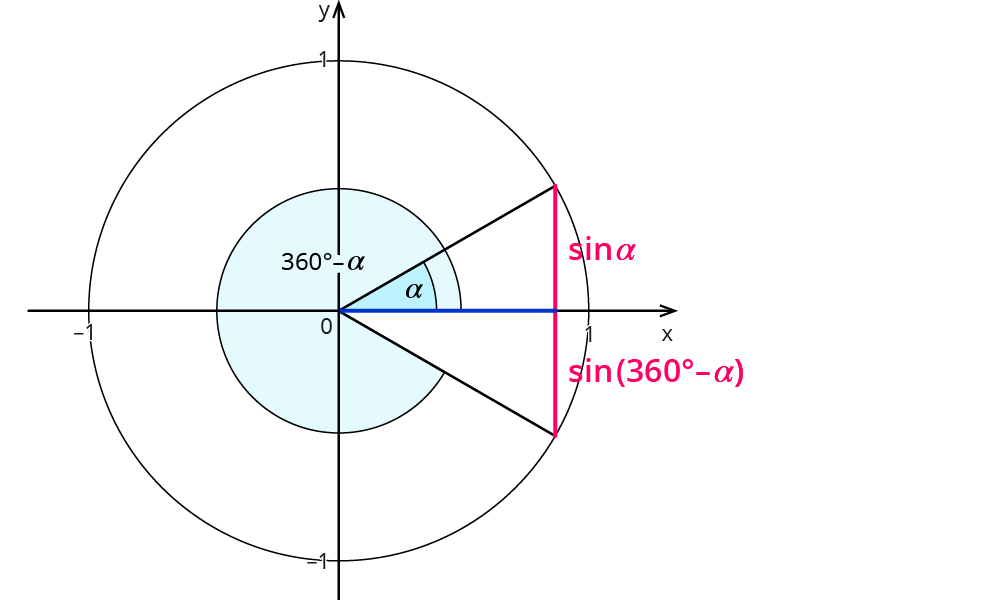
| Gradmaß | Bogenmaß |
| $$sin(alpha)=-sin(360^°-alpha)$$ | $$sin(x)=-sin(2pi-x)$$ |
Für den Kosinus
Solche Beziehungen findest du auch für den Kosinus.
Beispiel:
$$cos(30^°)=0,87$$ und $$cos(210^°)=-0,87$$.
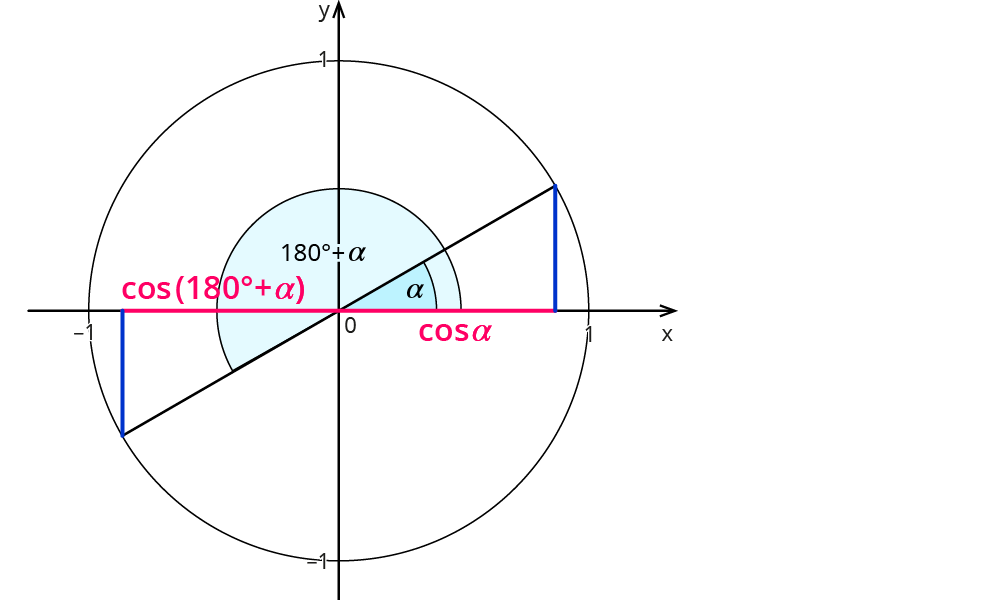
Allgemein gilt:
| Gradmaß | Bogenmaß |
| $$cos(alpha)=-cos(180^°+alpha)$$ | $$cos(x)=-cos(pi+x)$$ |
Und diese Beziehung hier:
Beispiel:
$$cos(30^°)=0,87$$ und $$cos(330^°)=0,87$$.
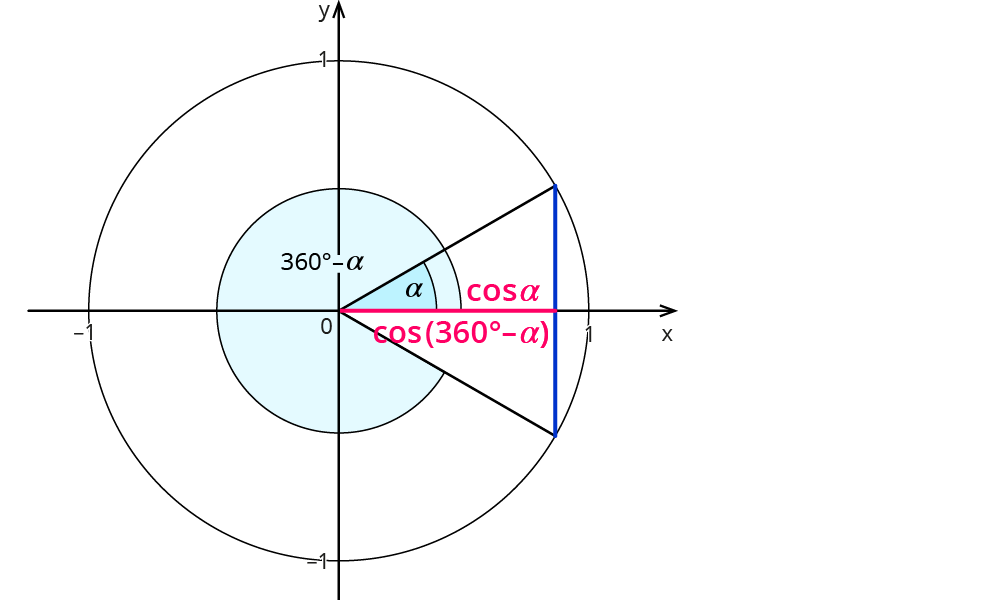
So sieht’s allgemein aus:
| Gradmaß | Bogenmaß |
| $$cos(alpha)=cos(360^°-alpha)$$ | $$cos(x)=cos(2pi-x)$$ |

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen