Statistische Daten durch Flächen und Körper darstellen
Daten und Diagramme
Du kennst bestimmt den Spruch: „Traue nie einer Statistik, die du nicht selbst gefälscht hast.“
Leute irrezuführen passiert häufig mit Flächen- und Körperdiagrammen, beabsichtigt oder unbeabsichtigt. Mehr dazu gleich.
Zur Erinnerung: Diagrammtypen
Diese Diagramme kennst du schon:
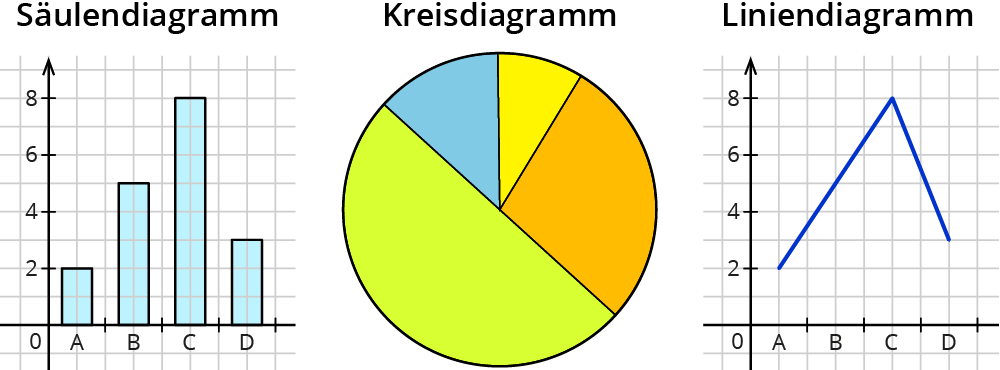
Mithilfe von Säulendiagrammen lassen sich Daten gut vergleichen. Ist eine Verteilung innerhalb einer Gesamtmenge von Interesse, werden oft Kreisdiagramme verwendet. Eine Veränderung von Daten lässt sich vorteilhaft in Liniendiagrammen veranschaulichen.
Tricks mit Daten
In Diagrammen können fehlerhafte Interpretationen auftreten:
- Die Achsenwerte beginnen nicht bei 0.
- Die Achseneinteilung ist ungleichmäßig.
Oder: Wenn beim Erstellen von Flächen- und Körperdiagrammen nicht richtig gerechnet wird!
Flächendiagramme
Aus einer Tageszeitung:
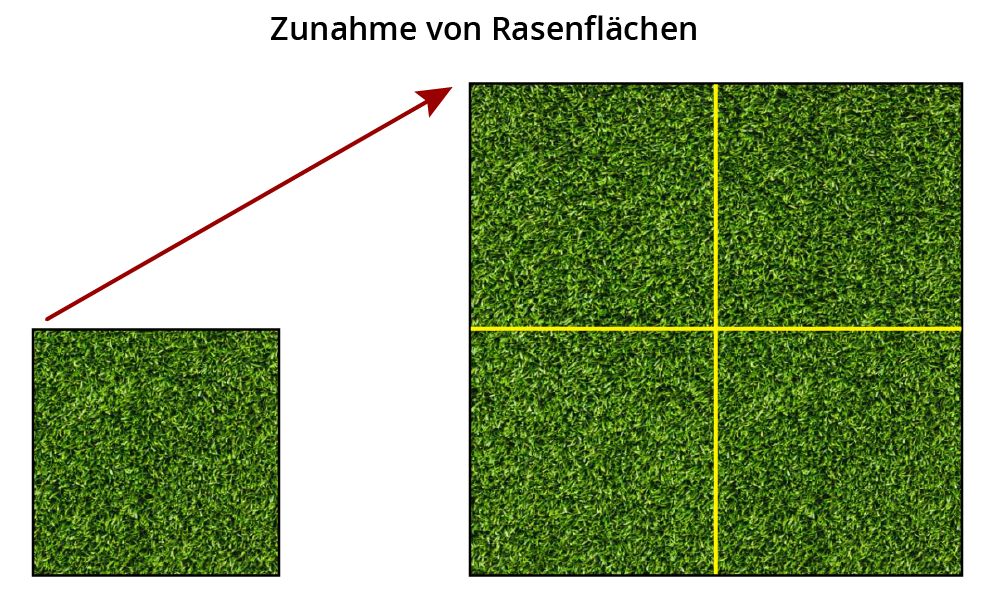
Nach neuen Informationen konnte die Rasenfläche in Wohnanlagen in den letzten 5 Jahren verdoppelt werden.

Passt die Grafik zum Text?
Hier die Antwort: Die Seitenlänge der Rasenfläche wurde zwar verdoppelt. Damit wird aber der Flächeninhalt vervierfacht!
Der optische Eindruck stimmt nicht mit der Aussage überein. Die Verdoppelung wird zu stark dargestellt.
Wenn du’s genauer wissen willst:
Die Begründung folgt aus der Ähnlichkeit von geometrischen Figuren.
Wird die Seitenlänge einer geometrischen Figur mit dem Faktor $$k$$ vergrößert, so wird der Flächeninhalt mit dem Faktor $$k^2$$ vergrößert:
Für ein Rechteck mit $$A = a * b$$ folgt bei Vervielfachung jeder Seitenlänge durch eine Multiplikation mit $$k$$:
$$A’=(k*a)*(k*b) = k^2 * a*b = k^2*A $$.
Körperdiagramme
Und noch eine Schlagzeile:
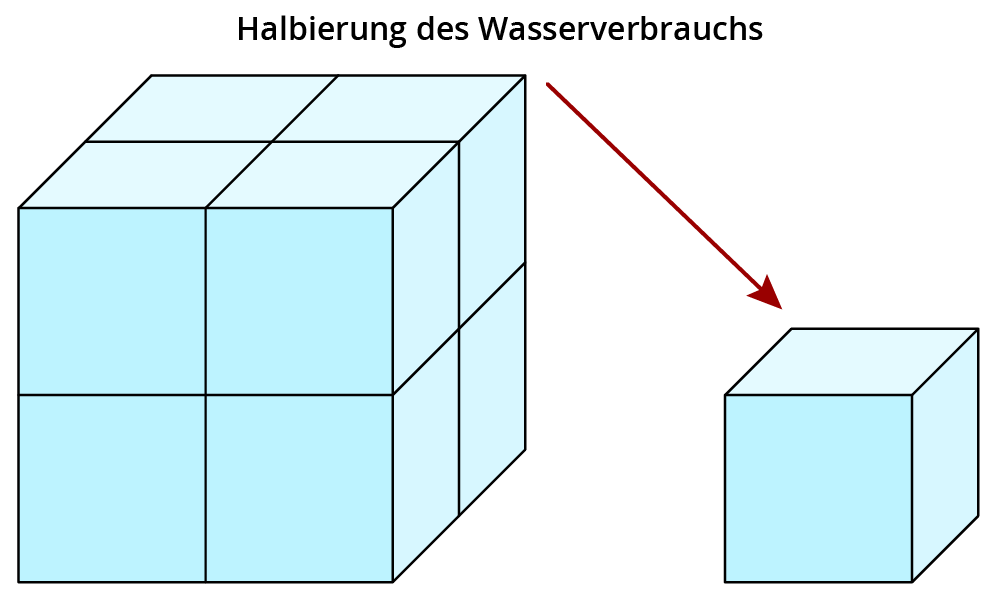
Durch Anwendung neuer Technologien konnte der Wasserverbrauch in den letzten 5 Jahren halbiert werden.
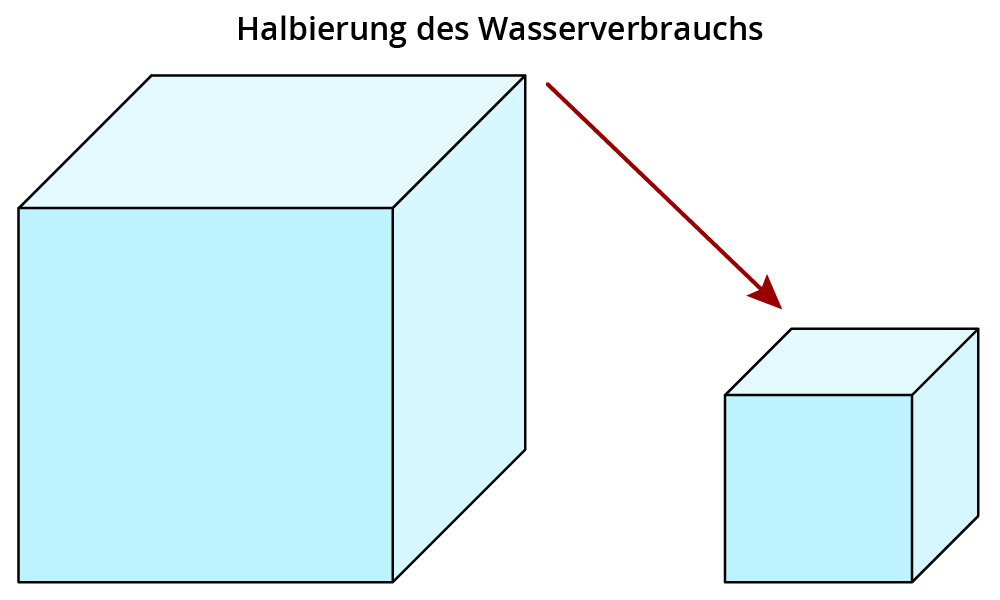
Passt die Grafik zum Text?
Und auch hier die Antwort: Jede Seitenlänge des Würfels wurde halbiert. Damit beträgt das Volumen des kleinen Würfels nur ein Achtel des Volumens des großen Würfels. Der optische Eindruck stimmt daher mit der Aussage nicht überein, die Verringerung ist übertrieben dargestellt.
Wenn du’s genauer wissen willst:
Die Begründung folgt wieder aus der Ähnlichkeit geometrischer Körper.
Wird die Seitenlänge eines geometrischen Körpers mit dem Faktor $$k$$ vergrößert, so wird das Volumen mit dem Faktor $$k^3$$ vergrößert.
Für einen Quader mit $$V = a * b * c$$ folgt bei Vervielfachung jeder Seitenlänge durch eine Multiplikation mit $$k$$: $$V’=(k*a)*(k*b)*(k*c) = k^3 * a*b*c = k^3*V $$.
Umgekehrt gilt: Wird jede Seitenlänge eines geometrischen Körpers um den Faktor $$k$$ verkleinert, verkleinert sich das Volumen um den Faktor $$k^3$$.
Für einen Quader mit $$V = a * b * c$$ folgt damit: $$V’=(a/k)*(b/k)*(c/k) = 1/k^3 * a*b*c = V/k^3 $$.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Und wie ist es richtig?
Willst du Daten mit Flächen- bzw. Körperdiagrammen angemessen darstellen, rechnest du mit Flächeninhalt und Volumen, nicht mit den Seitenlängen.
Flächendiagramm
Für die verdoppelte Rasenfläche:
Wenn eine Seite der Ausgangsfläche z. B. 2 cm lang ist, beträgt die Fläche
4 cm². Dann beträgt die doppelte Fläche 8 cm².
Wie lang ist dann eine Seite der quadratischen Fläche?
Ziehe die Wurzel: $$sqrt(8) cm approx 2,8 cm$$.
So sieht das passende Diagramm zu der Aussage aus:
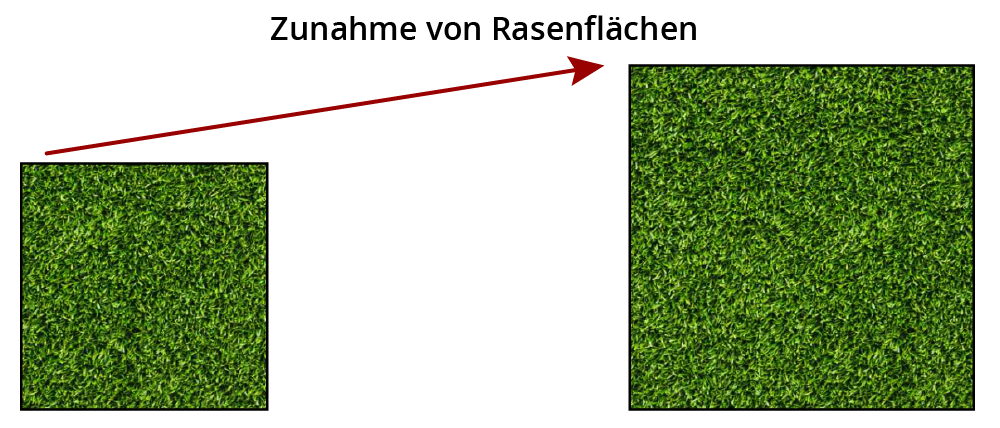
Körperdiagramm
Für den halbierten Wasserverbrauch:
Wenn das Ausgangsvolumen z. B. 8 cm³ ist, beträgt eine Seitenlänge des Würfels 2 cm. Das halbe Volumen beträgt 4 cm³.
Wie lang ist dann eine Seite des Würfels?
Ziehe die 3. Wurzel: $$root 3 (4) cm approx 1,6 cm$$.
So sieht das passende Diagramm zu der Aussage aus:
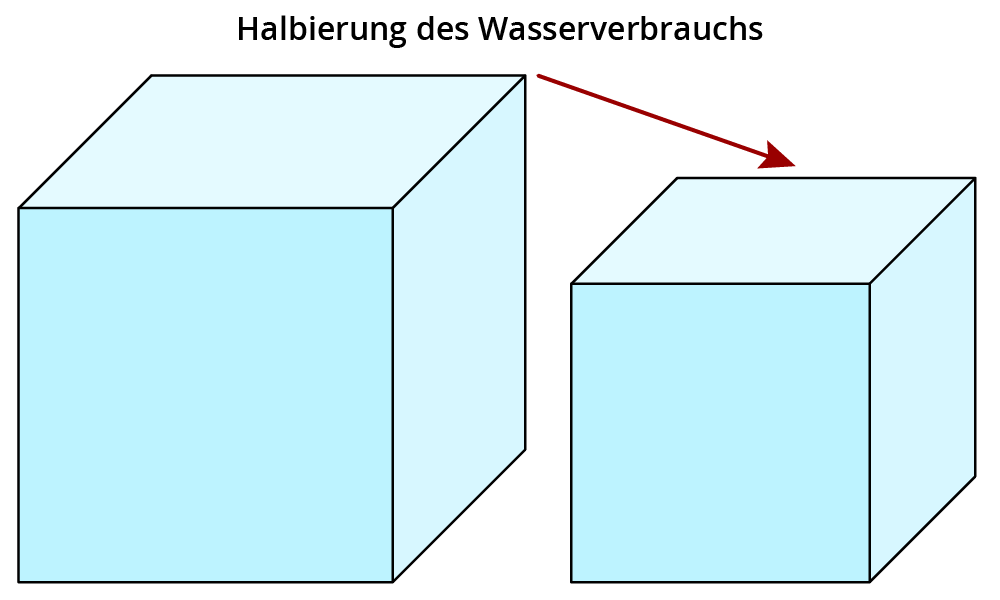
Darstellung von statistischen Daten durch Flächen und Körper
Flächen
Bei der Wahl von Flächen zur Veranschaulichung statistischer Daten muss der Flächeninhalt proportional zur dargestellten Größe (Ausgangsfläche) verändert werden:
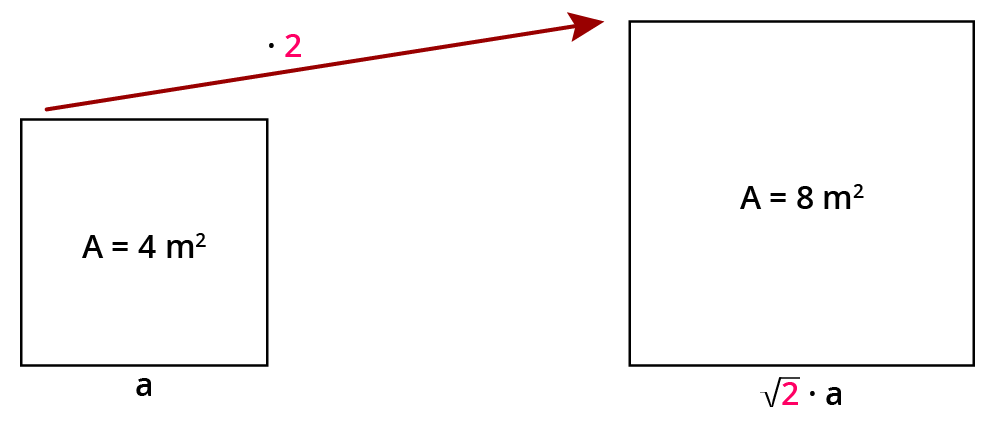
Wenn eine Fläche $$k$$-mal so groß ist wie die andere, muss die Seitenlänge mit dem Faktor $$sqrt(k)$$ multipliziert werden.
Körper
Bei der Wahl geometrischer Körper zur Veranschaulichung von statistischen Daten muss das Volumen proportional zur dargestellten Größe (Ausgangsvolumen) verändert werden:
Wenn ein Volumen $$k$$-mal so groß ist wie das andere, muss jede Seitenlänge des Körpers mit dem Faktor $$root(3)k$$ multipliziert werden.
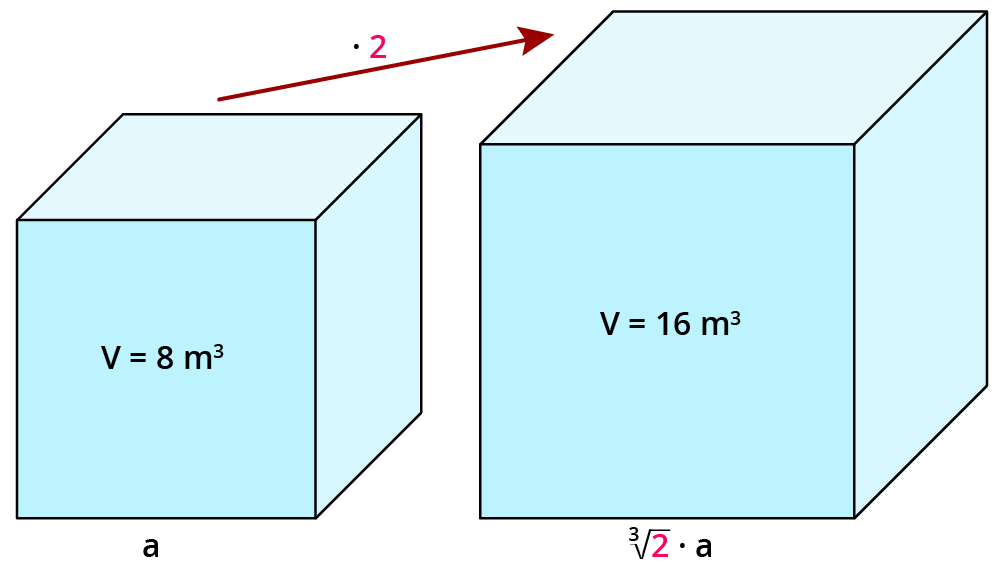
Wenn ein Volumen $$k$$-mal so groß ist wie das andere, muss jede Seitenlänge des Körpers mit dem Faktor $$root(3)k$$ multipliziert werden.
Das gilt nicht nur für Quadrat und Würfel, sondern auch für Rechteck und Quader.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen