Chancen und Risiken von Testverfahren abschätzen
Chancen und Risiken
Die Wahrscheinlichkeitsrechnung ist vor allem interessant, wenn es um Chancen und Risiken geht.
Beispiele:
- Ein Pharmaunternehmen schätzt die Chancen oder Risiken ein, wenn ein neues Medikament eingeführt wird.
- Eine Firma stellt Bauteile her und will die Chancen und Risiken verschiedener Qualitätskontrollen abschätzen.
- Casino-Betreiber berechnen, wie groß die Chance auf einen Gewinn bei den Glückspielen ist und wie groß das Risiko, zu verlieren. (Aus Sicht der Casino-Betreiber müssen die Kunden mehr verlieren als gewinnen.)
Für das Abschätzen von Chancen und Risiken vergleichst du die Wahrscheinlichkeiten von bestimmten Ereignissen.
Kurze Erinnerung: Wahrscheinlichkeiten bestimmen
Du würfelst einen Würfel einmal.
In beiden Fällen berechnest du die Wahrscheinlichkeit durch $$p = frac{\text{Anzahl günstige Fälle}}{\text{Anzahl mögliche Fälle}}$$.
Chancen und Risiken brauchst du vor allem bei Testverfahren. Los geht’s:
Testverfahren
Bestimmt hast du schon von Schwangerschaftstests gehört. Bei einer Schwangerschaft produziert der Körper ein bestimmtes Hormon und der Test prüft, ob dieses Hormon im Urin vorkommt.
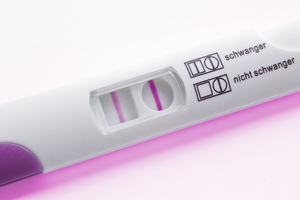
Bild: Panther Media GmbH (Thomas Lachemund)
Aber bei diesem Test und anderen medizinischen Tests gibt es ein Problem: Sie sind manchmal fehlerhaft. Es kommt vor, dass jemand schwanger ist, aber der Test das nicht anzeigt.
Diese „Testfehler“ müssen irgendwie erfasst oder abgeschätzt werden.
Hier sind erst mal die Fachbegriffe für Tests:
- Das Testergebnis ist positiv. Das heißt, der Test schlägt an. Hier ist positiv nicht im Sinn von „gut“ gemeint. Es heißt nur, dass der Test eine Reaktion zeigt.
- Das Testergebnis ist negativ. Bei dem Test gibt es keine Reaktion.
Für die Testergebnisse merke dir diese Fachbegriffe:
- richtig positiv: Jemand ist schwanger und der Test ist positiv
(Test zeigt „schwanger“ an). - falsch positiv: Jemand ist nicht schwanger, aber der Test ist positiv (Test zeigt „schwanger“ an).
- richtig negativ: Jemand ist nicht schwanger und der Test ist negativ (Test zeigt „nicht schwanger“ an).
- falsch negativ: jemand ist schwanger, aber der Test ist negativ (Test zeigt „nicht schwanger“ an).
Das Testergebnis stimmt also nicht bei „falsch positiv“ und „falsch negativ“ .
Hier siehst du die Wahrscheinlichkeiten für die Ergebnisse eines Schwangerschaftstests:
- richtig positiv: 98 %
- falsch positiv: 2 %
- richtig negativ: 99,99 %
- falsch negativ: 0,01 %
Du siehst, ein Schwangerschaftstest ist ziemlich genau.
Auf den Packungsbeilagen steht meistens nur eine Zahl: „über 99% sicher“. Die einzelnen Daten werden da in einen Topf geworfen.
Anwendungen für Tests
Solche Daten über Testergebnisse ermitteln Wissenschaftler oder Firmen für sehr viele Anwendungsbereiche: bei der Wirksamkeit von Medikamenten, bei der Diagnose von Krankheiten, bei Geräteprüfungen.
Interessant sind immer die falsch negativen und falsch positiven Testergebnisse.
Beispiele:
Es wird diagnostiziert, ob eine Person an einer Krankheit leidet.
- falsch negativ: Der Test ist negativ, obwohl die Person krank ist.
- falsch positiv: Der Test ist positiv, obwohl die Person gesund ist.
Ein Gerät wird auf Mängel überprüft.
- falsch negativ: Der Test ist negativ, obwohl das Gerät defekt ist.
- falsch positiv: Der Test ist positiv, obwohl das Gerät intakt ist.
Kleine Fehlerquoten wie 2 % hören sich zwar erst mal wenig an. Aber bei 100.000 Personen sind 2 % schon 2000 Personen! Und wenn bei einer Krankheit eine falsche Diagnose gestellt wird, kann die Person nicht gut behandelt werden.
Jetzt kommen 2 Beispiele. Beim Rechnen nimmst du am besten eine Tabelle oder ein Organigramm. Du kannst dir aussuchen, was dir lieber ist.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beispiel 1: Medizin-Test
Ein neuer Test für eine seltene Krankheit wurde bei 10.000 Personen angewendet. Die Ausgangslage für die Beurteilung ist:
83 von 10.000 leiden an der Krankheit, bei 75 der 83 fällt der Test positiv aus. Bei 265 gesunden Personen fällt der Test ebenfalls positiv aus.
Trage die Informationen in eine Tabelle ein. Berechne die fehlenden Daten mit Summen- bzw. Differenzbildung.
| krank | gesund | Summe | |
|---|---|---|---|
| Test positiv | |||
| Test negativ | |||
| Summe |
Aus den Daten folgt:
- Von 10.000 Personen fällt der Test bei 340 Personen positiv aus, wobei aber nur 75 von diesen, also etwa 22 %, tatsächlich krank sind.
- Andererseits sind 9.652 Personen von 9.660, also 99,9 %, mit negativem Testergebnis gesund.
- Eine Person mit negativem Testergebnis hat also eine fast 100%-ige Chance, gesund zu sein, während für eine Person mit positivem Testergebnis noch eine Chance von 78 % besteht, doch gesund zu sein.

Bild: Asea Brown Boveri (Viktor Cap)
Beispiel 2: Qualitätskontrolle

Bild: fotolia.com (industrieblick)
Eine Elektronik-Firma stellt immer Serien von 1.000 Bauteilen einer Sorte her. Aus Erfahrung ist bekannt, dass von einer Serie 40 Teile defekt sind. Bei der Endkontrolle werden mit einem Testverfahren 32 davon auch erkannt (Test positiv). Die Firma geht mit dem Test das Risiko ein, dass von den intakten Bauteilen 96 fälschlicherweise als defekt (Test positiv) eingestuft werden.
a) Wie viele der Bauteile, für die der Test positiv ausfällt, sind tatsächlich defekt?
b) Wie viele der Bauteile, für die der Test negativ ausfällt, sind tatsächlich intakt?
Lösung mit Organigramm:
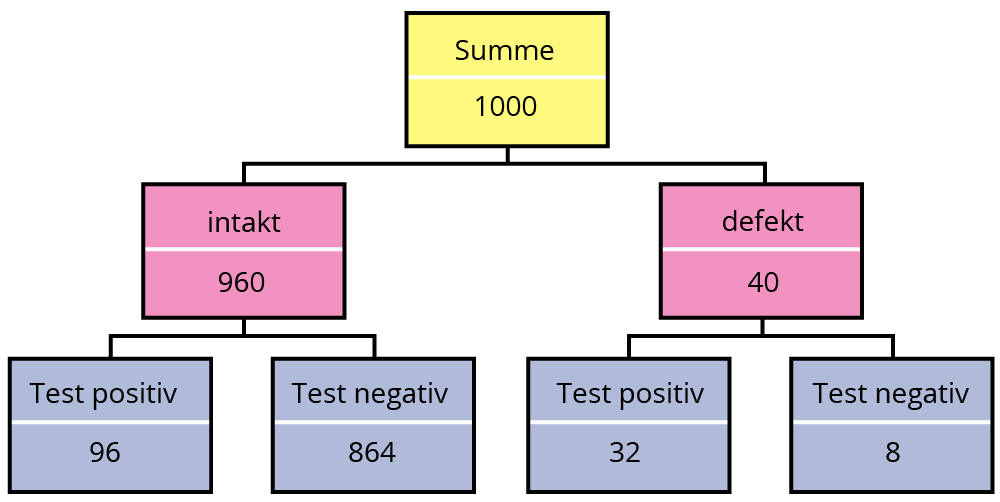
Zu a: Die Anzahl der Bauteile, für die der Test positiv ausfällt und die tatsächlich defekt sind, beträgt 32.
Zu b: Die Anzahl der Bauteile, für die der Test negativ ausfällt und die tatsächlich intakt sind, beträgt 864.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen