Pascalsches Dreieck
Pascalsches Dreieck
Erinnerst du dich noch an die erste binomische Formel:
$$(a + b)^2 = a^2 + 2ab + b^2$$ ?
Denken wir ein wenig weiter:
$$(a + b)^0$$
$$(a + b)^1$$
$$(a + b)^2$$
$$(a + b)^3$$
$$…$$
Was ergibt sich für diese Reihe?
$$(a + b)^0 = 1$$
$$(a + b)^1 = 1*a+1*b$$
$$(a + b)^2 = 1*a^2+2*ab+1*b^2$$
$$(a + b)^3 = 1*a^3+3*a^2b+3*ab^2+1*b^3$$
$$(a + b)^4 = …$$
Die Koeffizienten vor den einzelnen Summanden
sehen wir uns nun etwas näher an
$$1$$
$$1$$$$*a +$$$$1$$$$*b$$
$$1$$$$*a^2+$$$$2$$$$*ab +$$$$1$$$$*b^2$$
$$$$$$1$$$$*a^3+$$$$3$$$$*a^2b+$$$$3$$$$*ab^2+$$$$1$$$$*b^3$$
$$ …$$
und notieren sie in Form eines Dreiecks:
$$1$$
$$1$$ $$1$$
$$1$$ $$2$$ $$1$$
$$1$$ $$3$$ $$3$$ $$1$$
$$…$$
Zur Entstehung des Dreiecks
$$1$$
$$1$$ $$2$$ $$1$$
$$1$$ $$3$$ $$3$$ $$1$$
Aus den ersten drei Zeilen kannst du schon
erkennen:
- In jeder Zeile steht außen immer eine 1.
- Ein Koeffizient in einer Zeile folgt durch Addition der beiden Koeffizienten in der Zeile darüber.
Blaise Pascal (1623 - 1662)
Das nach Pascal benannte Dreieck war schon vor mehr als 1000 Jahren bekannt. Er hat es aber als erster systematisch untersucht.
Werden diese beiden Regeln angewendet, so erhältst du zum Beispiel aus den ersten drei Zeilen die folgenden Zeilen:
Das Pascalsche Dreieck
Nun kannst du die Regeln weiter anwenden und erhältst das folgende Schema des Pascalschen Dreiecks:

Wenn du Lust hast, kannst du weitere Zeilen hinzufügen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Besonderheiten des Pascalschen Dreiecks (1)
Die Zeilensumme
Wenn du die Summe aller Zahlen in einer Zeile bildest, erhältst du eine Zahlenfolge - beachte, dass die 1. Zeile als Zeile 0 bezeichnet wird:
Zeile 0: $$1 = 1$$
Zeile 1: $$1 + 1 =2$$
Zeile 2: $$1 + 2 + 1 =4$$
Zeile 3: $$1 + 3 + 3 + 1 =8$$
Zeile 4: $$1 + 4 + 6 + 4 + 1 = 16$$
$$…$$
Du erkennst bestimmt, dass sich die Summe der Zahlen von Zeile zu Zeile verdoppelt. Wenn du im Pascalschen Dreieck als Index $$n$$ den Exponenten des Binoms $$(a + b)$$ wählst, so kannst du das allgemeine Bildungsgesetz für die Summe $$S$$ der Zahlen aus dem folgenden Schema erkennen:
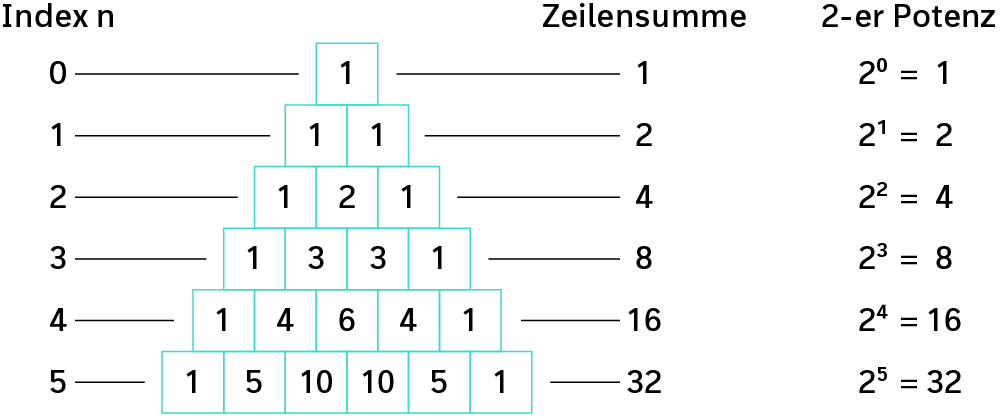
Wenn $$n$$ der Exponent des Binoms $$(a + b)$$ ist, so lautet das Bildgesetz für die Zeilensumme $$S$$ der Zahlen $$S = 2^n$$.
Beispiele:
$$2^0=1$$ (beachte die Festsetzung: jede Zahl hoch $$0$$ ergibt $$1$$)
oder
$$2^3 = 2 * 2 * 2 = 8$$
Besonderheiten des Pascalschen Dreiecks (2)
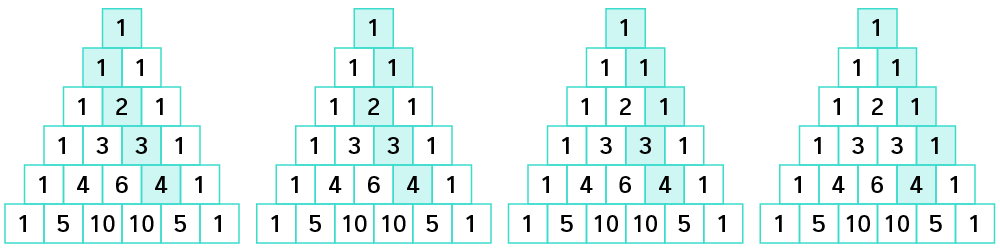
Viele Wege führen zum Ziel
Betrachte die $$1$$ im ersten Feld des Dreiecks von oben als Startpunkt. Nun zähle die Wege von „oben nach unten“ zum Feld mit der $$2$$. Du kannst nur auf zwei kürzesten Wegen dorthin kommen.
Die Abbildung oben zeigt dir, dass es vom Startpunkt $$1$$ zum Feld mit der $$4$$ genau $$4$$ kürzeste Wege gibt.
Probiere es mit anderen Zielen aus! Du wirst merken, dass dies immer gilt.
Besonderheiten des Pascalschen Dreiecks (3)
Teilbarkeitsmuster von Zahlen
Es werden nun die Zahlen im Pascalschen Dreieck markiert, die gerade sind - also alle durch $$2$$ teilbaren Zahlen. Diese Darstellung ist mal etwas anders - und sieht vielleicht hübscher aus!
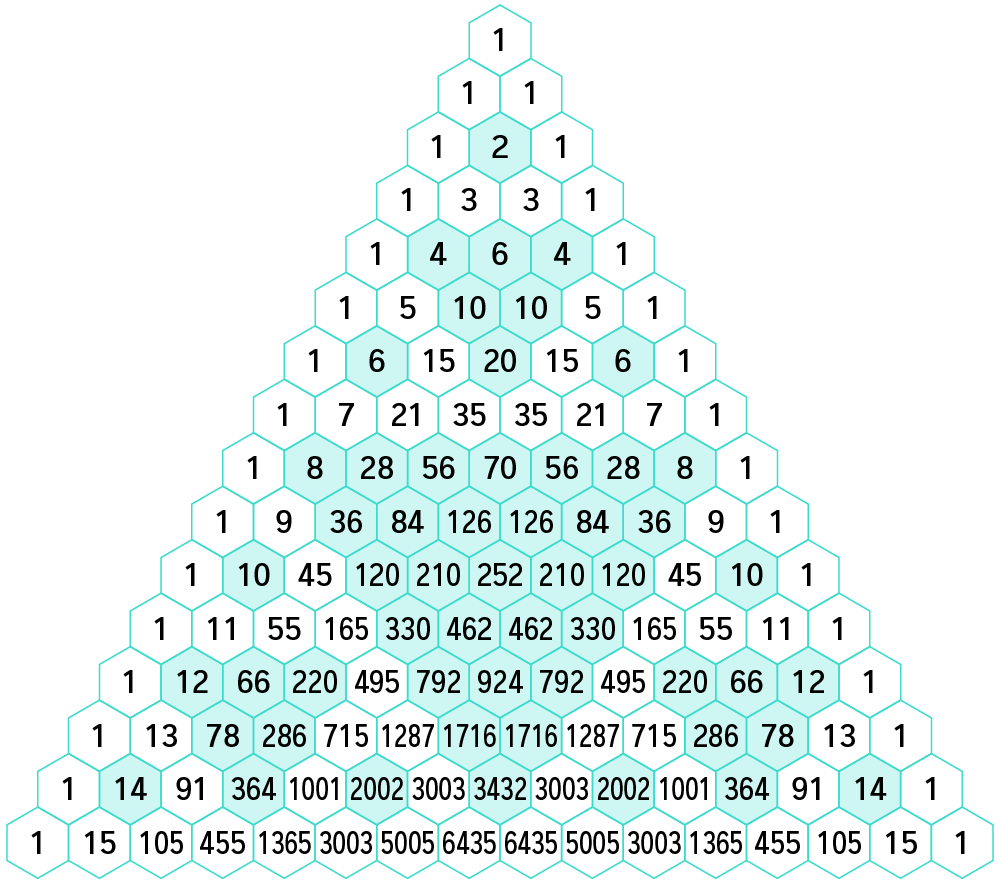
Es entstehen offenbar lauter Dreiecke, die zum Originaldreieck umgekehrt orientiert sind.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Besonderheiten des Pascalschen Dreiecks (4)
Quadratzahlen
Schau dir die nebenstehende Form der Zahlen des Pascalschen Dreiecks an. Beachte die dritte Spalte mit der Zahlenfolge
$$1, 3, 6, 10, 15, …$$
Wenn du je zwei aufeinanderfolgender Zahlen addierst, also
$$1 + 3$$ oder $$3 + 6$$ oder $$10 + 15$$, erhältst du eine Quadratzahl.
Eine andere Form der Darstellung der Zahlen des Pascalschen Dreieck ist die folgende:
$$1$$
$$1 1$$
$$1 2 1$$
$$1 3 3 1$$
$$1 4 6 4 1$$
$$1 5 10 10 5 1$$
$$1 6 15 20 15 6 1$$
Fibonacci-Zahlen

Schau dir die durch die Diagonalen markierten Zahlen an und bilde jeweils die Summe. Es entsteht wieder eine Zahlenfolge, die sogenannte Fibonacci-Folge:
$$1, 1, 2, 3, 5, 8, …$$.
Jede Fibonacci-Zahl ergibt sich als Summe der beiden vorhergehenden Fibonacci-Zahlen. Auch diese Zahlenfolge hat eine Vielzahl von Beziehungen zu anderen Bereichen der Mathematik. Informiere dich im Internet über diese Zahlenreihe.
Es gibt noch viele weitere Besonderheiten des Pascalschen Dreiecks. Vielleicht gibt es in den Übungen noch etwas - lass dich überraschen!
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



