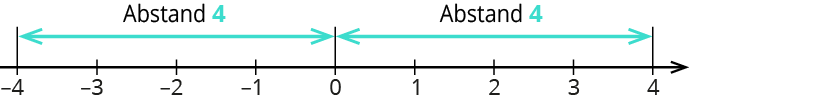Umkehrrechenarten nutzen
Die additive Gegenzahl
Die additive Gegenzahl zu $$a$$ ist $$–a$$. Als Gegenzahl bezeichnest du die Zahl, die in der Addition $$0$$ ergeben.
Beispiel:
Zu $$7$$ ist die Gegenzahl $$-7$$.
$$7+(-7)=0$$
Zu $$-5$$ ist die Gegenzahl $$5$$.
$$-5+5=0$$
$$0$$ ist das neutrale Element der Addition und Subtraktion. Der Wert des Ergebnisses ändert sich durch $$+ 0$$ nicht.
Beispiel: $$8 + 0 = 8$$
In dem Zahlbereich der natürlichen Zahlen gibt es keine Gegenzahlen. Denn alle natürlichen Zahlen sind nicht negativ.
Die multiplikative Gegenzahl
Die multiplikative Gegenzahl zu $$a$$ ist $$1/a$$. Beim Multiplizieren ergeben Zahl und Gegenzahl $$1$$.
Beispiel:
Zu $$3$$ ist die Gegenzahl $$1/3$$.
$$3*1/3=1$$
Betrag einer Zahl
Der Betrag einer Zahl ist der Abstand von der $$0$$. Du schreibst den Betrag einer Zahl in Betragsstriche. $$|x|$$
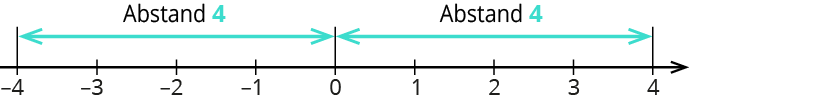
Beispiel:
$$|4| = 4$$
$$|-4| = 4$$
Beide Zahlen haben denselben Abstand von der $$0$$.
Bei positiven Zahlen kannst du den Betragsstrich weglassen. Bei negativen Zahlen in Betragsstrichen erhältst du eine positive Zahl.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Nutzen
Mit den Gegenzahlen kannst du Rechnungen vereinfachen.
Beispiel:
$$7 * 8 * 1/8 + 359 – 7 = 359$$
Du siehst gleich, dass $$8 * 1/8 = 1$$ ist.
$$7 – 7 = 0$$
Das Ergebnis der Aufgabe ist $$359$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen