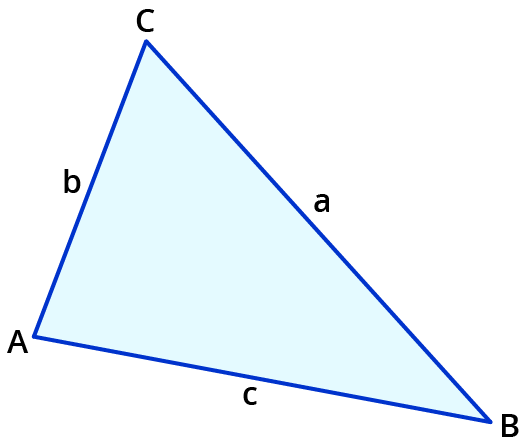
Den Kongruenzsatz SWS nutzen
Der Kongruenzsatz SWS (Seite - Winkel - Seite)
Und noch ein Kongruenzsatz:
Kongruenzsatz sws
Stimmen zwei Dreiecke in zwei ihrer Seiten (S) und dem von diesen Seiten eingeschlossenen Winkel (W) überein, so sind sie kongruent zueinander.
Damit ist der Kongruenzsatz SWS in den folgenden Fällen anwendbar:
1. gegeben: a, b, $$gamma$$
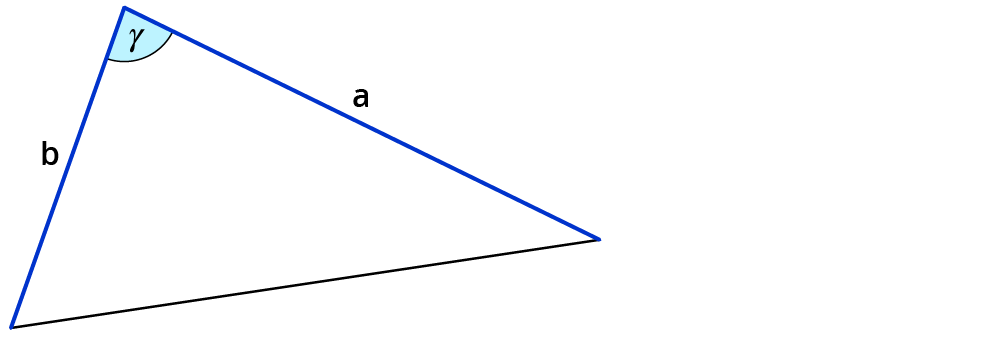
2. gegeben: b, c, $$alpha$$

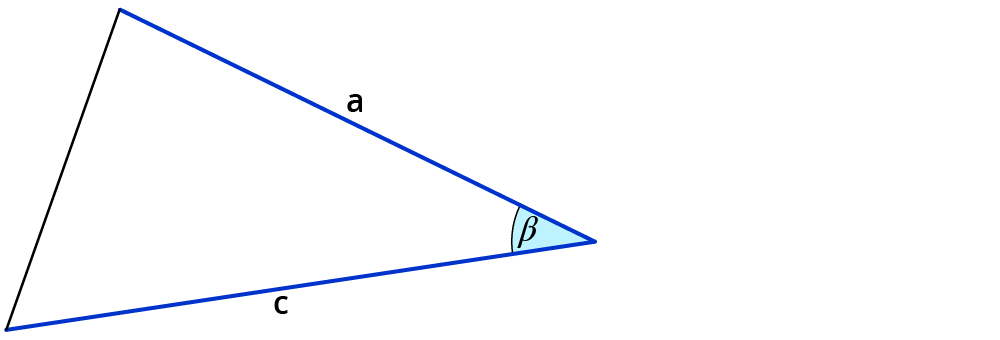
3. gegeben: c, a, $$beta$$
Beispiele
Beispiel 1:
Dreieck 1: a = 4,5 cm, b = 3,8 cm, $$gamma$$ = 57°
Dreieck 2: a = 4,5 cm, b = 3,8 cm, $$gamma$$ = 57°
Offensichtlich sind Dreieck 1 und Dreieck 2 jetzt nach dem Kongruenzsatz SWS kongruent zueinander, denn sie stimmen in den zwei Seiten a und b und dem eingeschlossenen Winkel $$gamma$$ überein.
Beispiel 2:
Dreieck 3: a = 4,5 cm, b = 3,8 cm, $$gamma$$ = 57°
Dreieck 4: b = 3,8 cm, c = 4,5 cm, $$alpha$$ = 57°
Auch Dreieck 3 und Dreieck 4 sind jetzt nach dem Kongruenzsatz SWS zueinander kongruent, wenn man beachtet, dass der Winkel $$gamma$$ von den beiden Seiten a und b und der Winkel $$alpha$$ von den beiden Seiten b und c eingeschlossen wird.
Beispiel 3:
Dreieck 5: a = 4,5 cm, b = 3,8 cm, $$gamma$$ = 57°
Dreieck 6: a = 3,8 cm, b = 4,5 cm, $$gamma$$ = 57°
Auch hier kannst Du den Kongruenzsatz SWS anwenden, da nur die beiden Längen a und b vertauscht sind, die sich ergebenden Dreiecke also spiegelbildlich zueinander sind.
Beispiel 4:
Dreieck 7: a = 4,5 cm, b = 3,8 cm, $$gamma$$ = 57°
Dreieck 8: b = 4.5 cm, c = 3,8 cm, $$gamma$$ = 57°
Auf den ersten Blick sieht es hier so aus, als könnest du den Kongruenzsatz SWS anwenden, aber bei genauerem Hinsehen stellst du fest, dass der Winkel $$gamma$$ zwischen den beiden Seiten a und b, nicht aber zwischen b und c liegt. Für Dreieck 8 müsste also der Winkel $$alpha$$, nicht der Winkel $$gamma$$ gegeben sein. Der Kongruenzsatz SWS ist demzufolge für die Dreiecke 7 und 8 nicht anwendbar.
Konstruieren mit dem Kongruenzsatz SWS
So konstruierst du ein Dreieck mit SWS:
Konstruktionsbeschreibung
Konstruiere ein Dreieck mit den Seitenlängen a=5 cm, b = 3 cm und $$gamma$$ = 50°. Dazu gehst du folgendermaßen vor.
1. Schritt:
Zeichne die Seite b mit den Eckpunkten A und C.

2. Schritt:
Trage am Punkt C den Winkel $$gamma$$ ab und zeichne durch C die Gerade g.
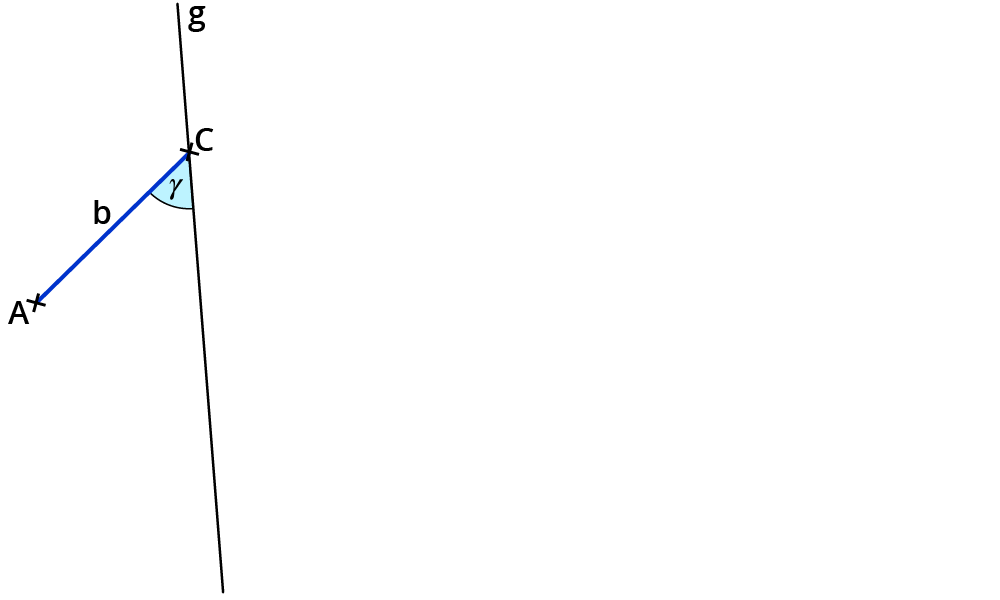
3. Schritt:
Trage auf g von C aus die Länge a ab und nenne den Endpunkt B.
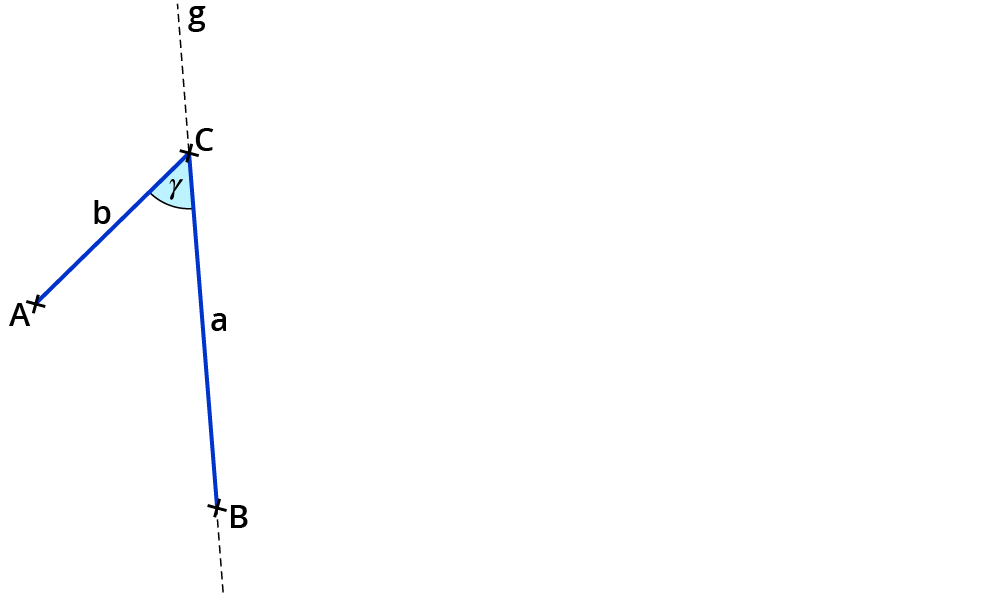
4. Schritt.:
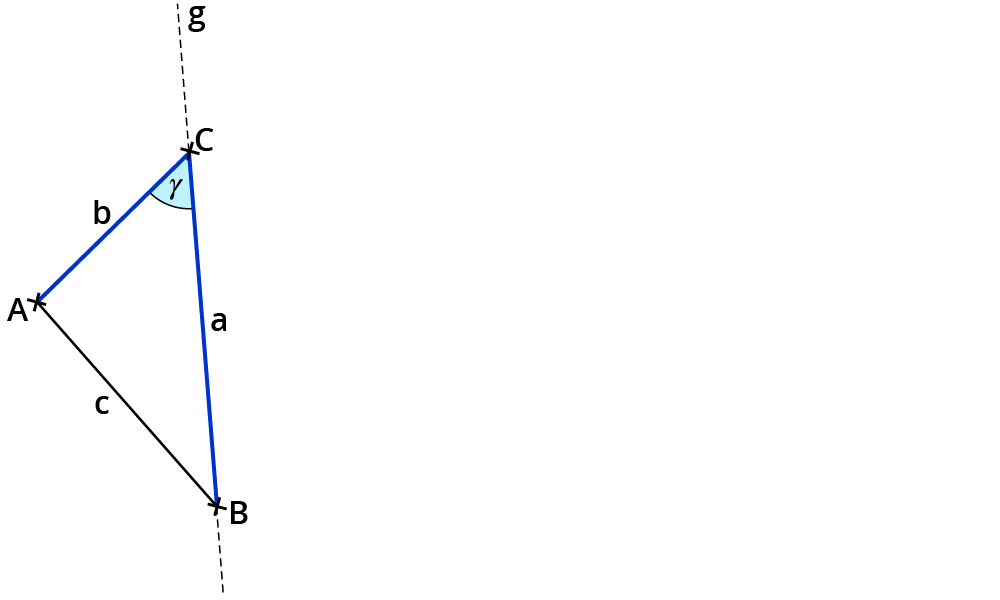
Verbinde die Punkte A und B zur Strecke c.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Allgemeines Vorgehen
Um die Konstruktion auch in den anderen Fällen durchführen zu können, gehst du so vor:
| gegeben | Schritt 1 | Schritt 2 | Schritt 3 | Schritt 4 |
|---|---|---|---|---|
| a, b, $$gamma$$ | b zeichnen | $$gamma$$ abtragen | a abtragen | c zeichnen |
| b, c, $$alpha$$ | c zeichnen | $$alpha$$ abtragen | b abtragen | a zeichnen |
| c, a, $$beta$$ | a zeichnen | $$beta$$ abtragen | c abtragen | b zeichnen |
Beweis des Kongruenzsatzes SWS
Da sich der Winkel zwischen den beiden gegebenen Seiten befinden muss, besteht die einzige Möglichkeit mit den gegebenen Angaben Dreiecke auf verschiedene Arten zu zeichnen darin, diese beiden Seiten zu vertauschen. Fährst du dann mit der Konstruktion wie beschrieben fort, so erhältst du zwei zueinander spiegelbildliche Dreiecke. Solche Dreiecke sind aber zueinander kongruent.


kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen