Primfaktorzerlegung
Primfaktorzerlegung
Primzahlen kennst du schon: Es sind die Zahlen, die genau zwei Teiler haben. Primzahlen sind nur durch 1 und durch sich selbst teilbar.
Die Zahl 1 ist keine Primzahl. Sie hat nur einen Teiler, die 1.
Das sind alle Primzahlen, die kleiner als 100 sind:
$$2$$ $$3$$ $$5$$ $$7$$
$$11$$ $$13$$ $$17$$ $$19$$
$$23$$ $$29$$
$$31$$ $$37$$
$$41$$ $$43$$ $$47$$
$$53$$ $$59$$
$$61$$ $$67$$
$$71$$ $$73$$ $$79$$
$$83$$ $$89$$
$$97$$
Du kannst alle natürlichen Zahlen als Produkt von Primzahlen schreiben. Klingt erstmal nicht so spannend, kann aber praktisch zum Rechnen sein.
Beispiele:
Die Zahlen 15 und 66 mit ihrer Primfaktorzerlegung:
$$15=3*5$$
$$66=2*3*11$$
Rechts vom $$=$$ stehen nur Primzahlen: 3 und 5 für die 15 oder 2 und 3 und 11 für die 66.
Jede natürliche Zahl, die selbst keine Primzahl ist, kannst du in ein Produkt von Primzahlen zerlegen.
Selber Primfaktorzerlegung finden
Wie findest du die Primfaktorzerlegung einer Zahl?
Aufgabe: Schreibe 108 als Produkt von Primzahlen.
Finde eine Zahl, durch die die 108 teilbar ist. 108 ist eine gerade Zahl, also ist sie durch 2 teilbar.
$$108 = 2*54$$
54 ist auch gerade. Also teile 54 durch 2.
$$108 = 2*2*27$$
Die Zahl 27 ist durch 3 teilbar. Teile 27 durch 3.
$$108 = 2*2*3*9$$
Die Zahl 9 ist durch 3 teilbar
$$108=2 * 2 * 3 * 3 * 3$$
Die Faktoren rechts kannst du nicht weiter zerlegen. Das sind jetzt alles Primzahlen.
Schreibe die Primfaktorzerlegung noch kürzer auf: mit der Potenzschreibweise.
$$108 = 2^2* 3^3$$
Du siehst einer Zahl gut an,
- ob sie durch 2 teilbar ist: letzte Ziffer gerade
- ob sie durch 5 teilbar ist: letzte Ziffer 0 oder 5
- ob sie durch 10 teilbar ist: letzte Ziffer 0
- ob sie durch 3 teilbar ist: Quersumme durch 3
Wenn ein Teiler mehrfach vorkommt, verwende die Potenzschreibweise.
Beispiel:
$$100 = 2^2 * 5^2$$.
Weißt du noch?
$$4^3 = 4 * 4 * 4$$
└──┬─┘
$$3$$-mal der Faktor $$4$$
Potenzen sehen immer so aus: 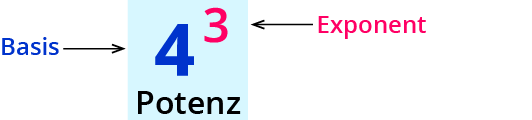
Lies: 4 hoch 3
Unterschiedliche Rechenwege
Es gibt unterschiedliche Rechenwege, die Primfaktorzerlegung zu finden.
Bei 108 kannst du auch erst durch 4 rechnen. (8 ist durch 4 teilbar und 100 auch.)
$$108=4*27$$
4 ist 2 mal 2.
$$108=2*2*27$$
27 ist durch 3 teilbar.
$$108=2*2*3*9$$
9 ist auch durch 3 teilbar.
$$108=2*2*3*3*3$$
Mit Potenzen:
$$108=2^2*3^3$$
Es gibt unterschiedliche Rechenwege, die Primfaktorzerlegung zu finden. Sie führen alle zum selben Ergebnis. Denn Faktoren kannst du in einem Produkt vertauschen (Kommutativgesetz).

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Noch ein Beispiel
Aufgabe: Schreibe 920 als Produkt von Primzahlen.
920 endet auf 0. Teile zuerst durch 10.
$$920= 10*92$$
10 kannst du als 2$$*$$5 schreiben.
$$920 = 2*5*92$$
92 ist eine gerade Zahl. Rechne durch 2.
$$920 = 2*5*2*46$$
46 ist eine gerade Zahl, also durch 2.
$$920 = 2*5*2*2*23$$
23 ist eine Primzahl. Du kannst nicht weiter zerlegen.
Schöner sieht’s noch in dieser Reihenfolge aus:
$$920 = 2*2*2*5*23$$
Und mit Potenzen:
$$920= 2^3*5*23$$
Wenn du eine Zahl in Primfaktoren zerlegst, teile so lange, bis nur noch Primzahlen im Produkt stehen.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



