Anwendungsaufgaben

Wenn du fit mit Volumen und Oberfläche von Quadern und Würfeln bist, kann es richtig losgehen: Tankfüllung, Wasserverbrauch, Ummantelung, Verpackungsmaterial, dabei entstehende Kosten… Von quaderförmigen Gegenständen kannst du das alles selbst berechnen!

Gesuchtes bestimmen

Aber wie siehst du der Aufgabe an, was du rechnen musst? Das ist ja immer das Schwierige… Stell dir die Aufgabe im Kopf vor. Und gucke im Text nach Signalwörtern.

Volumen

• Wie viel passt rein?
• Wie groß ist die Wassermenge?
• Fassungsvermögen
• Einheiten wie Liter, Milliliter, m³, dm³, …

Beispiel: Wie viel Liter fasst der Behälter?

Oberfläche

• Verpackungsmaterial
• Stoffbezug
• Einheiten wie km², m², dm²

Beispiel: Wie viel Geschenkpapier wird benötigt, um das Buch einzupacken?

Wenn du in einen Gegenstand was reinfüllst, berechnest du das Volumen. Beispiel: Wassermenge eines Aquariums

Wenn es um das Drumrum des Gegenstands geht, berechnest du den Oberflächeninhalt oder einzelne Flächen des Oberflächeninhalts.
Beispiel: Glasflächen fürs Aquarium, aber ohne die obere Deckfläche.

Schwimmbecken

In einem Schwimmbad müssen die Becken einmal im Jahr gründlich gereinigt werden. Dazu wird das Wasser komplett abgelassen und nach der Reinigung wird das Becken wieder gefüllt.
Ein normales Schwimmerbecken ist 50 m lang, 25 m breit und 2 m tief. Wenn das Becken mit Wasser gefüllt wird, schafft die Pumpe 32 m³ in der Stunde.
Wie lange dauert es mindestens, das Becken zu füllen?

Lösung:
Stell dir ein Schwimmbecken vor. Geometrisch ist das ein Quader. Du füllst das Schwimmbecken, also brauchst du das Volumen. Um die Pumpe kannst du dich danach kümmern. ☺

Die Formel für das Volumen eines Quaders ist

$$V=a*b*c$$

$$=50 * 25 *2 $$

$$= 1250 * 2$$

$$= 2500 \ m^³$$

Die Pumpe füllt pro Stunde 32 m³ ins Becken. Wie oft passen die 32 m³ in 2500 m³? Dann hast du die Stunden.

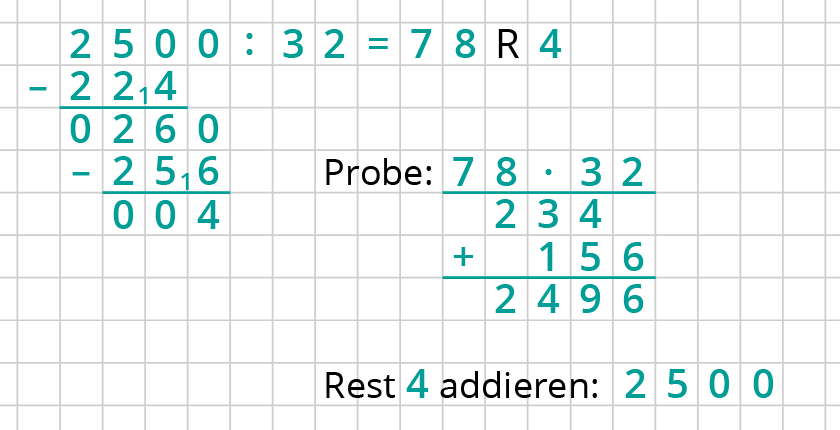
(Bei „echten“ Aufgaben gehen die Zahlen oft nicht auf…)

Die Pumpe braucht 78 Stunden und ein bisschen. Runde für deinen Antwortsatz dann immer nach oben auf.

Antwortsatz: Die Pumpe braucht 79 Stunden, bis das Becken gefüllt ist.

79 Stunden sind mehr als 3 Tage und wahrscheinlich soll die Pumpe nicht Tag und Nacht am Stück laufen. Wenn du’s genau haben willst, kannst du schreiben: Es dauert mindestens 79 Stunden, bis das Becken gefüllt ist.

Geschenke, Geschenke

Eine Firma stellt diese Geschenkkartons her.

Ein Drogeriemarkt bestellt 100 000 Kartons. Wie viel Verpackungsmaterial verbraucht die Firma für die Herstellung der Kartons?

Lösung:
Gesucht ist Verpackungsmaterial. Das heißt, du suchst den Oberflächeninhalt.
Der Karton besteht aus 2 Teilen. Dem unteren Teil und dem Deckel. Du kannst vernachlässigen, dass die Deckfläche ja eigentlich ein bisschen größer ist als die Grundfläche. Dazu stehen in der Aufgabe ja keine Größenangaben.
Also kannst du sagen: Der Karton ist mathematisch ein Würfel. Zu der Würfeloberfläche kommen noch die 2 cm hohen überstehenden Stücke von dem Deckel dazu.

Weiter geht’s mit der Rechnung:

Geschenke, Geschenke

Die Formel für den Oberflächeninhalt eines Würfels ist:

$$O=6*a^2$$

$$=6*10^2$$

$$=6*10*10$$

$$=600 \ cm^2$$

Es kommen 4 Streifen dazu, die 10 cm lang und 2 cm breit sind. Diese Streifen sind Rechtecke.

1 Streifen:

$$A=a*b$$

$$= 10*2$$

$$=20 \ cm^2$$

4 Streifen:

$$A=4*20 \ cm^2 = 80 \ cm^2$$

Ganzer Karton:

$$O=600 \ cm^2 + 80 \ cm^2 = 680 \ cm^2$$

Davon 100 000 Stück:

$$A = 100\ 000 * 680 \ cm^2 = 68\ 000 \ 000 \ cm^2$$

Bisschen groß die Zahl, wandle um:

$$68 \ 000 \ 000 \ cm^2 = 680 \ 000 \ dm^2 = 6800 \ m^2$$

Antwort: Die Firma benötigt 6800 m², um 100 000 Kartons herzustellen.