Vermischte Aufgaben Dezimalbrüche (Vorrangregeln)

Mathematik

Deutsch

Englisch

Rechenregeln

Rechnen geht nach bestimmten Regeln. Die gute Nachricht: Die Regeln, die du schon kennst, gelten ganz genau so auch für Dezimalbrüche.

Das sind die Vorrangregeln. Fast so wie im Straßenverkehr. :-)

Beispiele:

$$4,2:(0,7*2)=4,2:1,4=42:14=3$$

$$0,25*(4,0+0,4)=0,25*4,4=1,1$$

$$0,25*4,0+0,4=1,0+0,4=1,4$$

Vermischte Aufgaben Dezimalbrüche (Vorrangregeln)
Bild: Studio Schmidt-Lohmann

Ach ja, Potenzen gibt’s auch noch… Du kannst auch Dezimalbrüche potenzieren.

Potenzen rechnest du immer zuerst aus.

Beispiele:

$$5*1,2^2=5*1,44=7,2$$

$$(5*1,2)^2=6^2=36$$

$$5,6+4*1,1^2=5,6+4*1,21=5,6+4,84=10,44$$

Die Vorrangregeln:

Du kennst Potenzen als Produkte aus immer denselben Faktoren.
Für $$10*10*10$$ schreibst du $$10^3$$.

Eine Potenz sieht also immer so aus: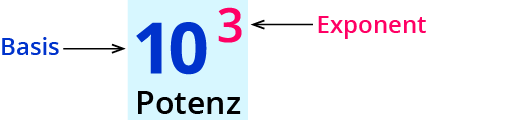

Vermischte Aufgaben Dezimalbrüche (Vorrangregeln)

Auch Vertauschungs- und Verbindungsgesetz gelten für Dezimalbrüche.

Regel	Beispiel
Vertauschungsgesetz
Beim Addieren kannst du die Summanden vertauschen. Das kann dir das Rechnen erleichtern.	$$1,2+2,9+1,8$$ $$=1,2+1,8+2,9$$ $$=5,9$$
Beim Multiplizieren kannst du die Faktoren vertauschen. Das kann dir das Rechnen erleichtern.	$$0,43,75$$ $$=0,453,7$$ $$=7,4$$
Verbindungsgesetz
Beim Addieren kannst du beliebig Klammern setzen oder weglassen. Das kann dir das Rechnen erleichtern.	$$5,6+2,3+1,7$$ $$=5,6+(2,3+1,7)$$ $$=5,6+4$$ $$=9,6$$
Beim Multiplizieren kannst du beliebig Klammern setzen oder weglassen. Das kann dir das Rechnen erleichtern.	$$1,20,80,5$$ $$=1,2(0,80,5)$$ $$=1,2*0,4$$ $$=0,48$$
Distributivgesetz
Wenn du eine Zahl mit einer Summe (Differenz) multiplizierst und wenn du diese Zahl mit den einzelnen Summanden multiplizierst, kommt das gleiche Ergebnis heraus. Das gilt auch für die Division.	$$1,5 * ( 2,4 + 0,6 ) $$ $$ =1,5 * 2,4 + 1,5 * 0,6$$ $$1,5 * ( 2,4 - 0,6 ) $$ $$= 1,5 * 2,4 - 1,5 * 0,6$$