Was ist eine Kugel?

Gegenstände, die kugelförmig sind (oder fast kugelförmig), kennst du schon jede Menge:

Und jetzt mathematisch:

Eine Kugel ist ein geometrischer Körper, den du erhältst, wenn du einen Kreis um seinen Durchmesser rotieren lässt.

Die Kugel hat einen Mittelpunkt. Alle Punkte der Oberfläche sind vom Mittelpunkt gleich weit entfernt. Der Abstand ist der Radius oder Kugelradius.

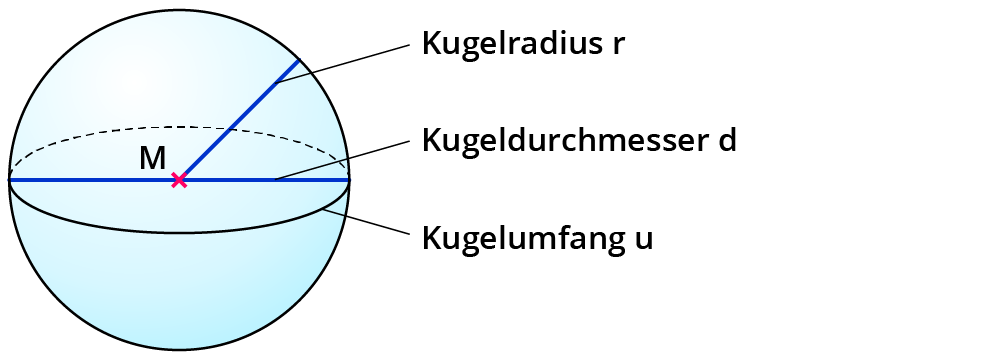
Was ist das Volumen einer Kugel?

Da die Kugel ein Körper ist, kann sie gefüllt werden.

Füllst du eine Kugel mit Wasser und misst dies in einem Messbecher, erhältst du das Volumen der Kugel. Das Volumen gibt dir an, wie viel Flüssigkeit in eine Kugel passt. Für Ballon und Fußball berechnest du, wie viel Luft du zum Füllen brauchst.

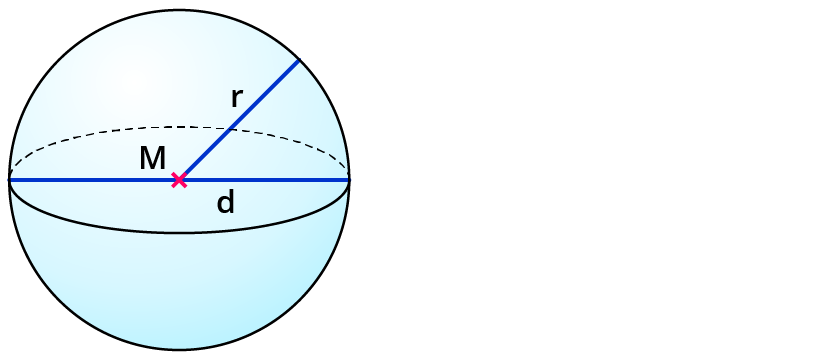
• r Radius
• d Durchmesser
• π Kreiszahl

Volumen einer Kugel berechnen

Gegeben ist eine Kugel mit d = 8 cm.

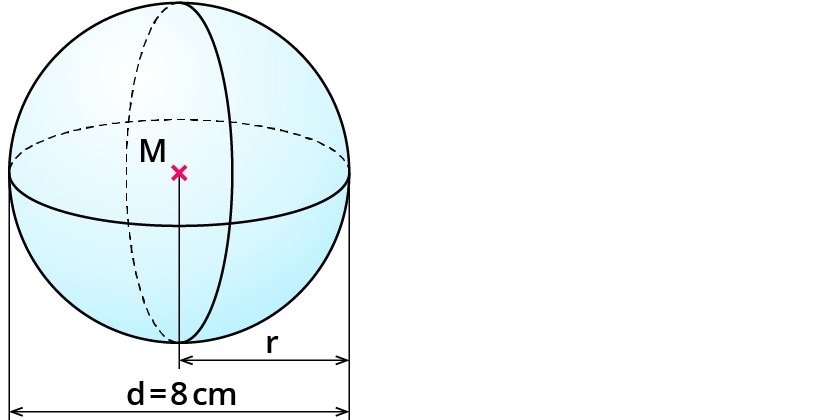
$$d = 2 * r$$

$$Leftrightarrow$$ $$d/2 = r$$

$$Leftrightarrow$$ $$(8  cm)/2 = r$$

$$Leftrightarrow$$ $$4$$ $$cm = r$$

Um das Volumen der Kugel zu berechnen, gehst du so vor:

$$V = 4/3pi * r^3$$

$$V = 4/3pi * (4$$ $$cm)^3$$

$$V = 4/3pi * 64 $$ $$cm^3$$

$$V = 268,08$$ $$cm^3$$

Trick für die Probe

Als Kontrolle, ob du richtig gerechnet hast, kannst du folgenden Trick verwenden:

Das Kugelvolumen ist ungefähr halb so groß wie das Volumen eines umbauten Würfels mit einer Kantenlänge so lang wie der Durchmesser d. Dies kannst du schnell im Kopf nachrechnen:

Kugelvolumen $$≈ 1/2$$ Würfelvolumen

$$V_K ≈ 1/2$$ $$V_W$$

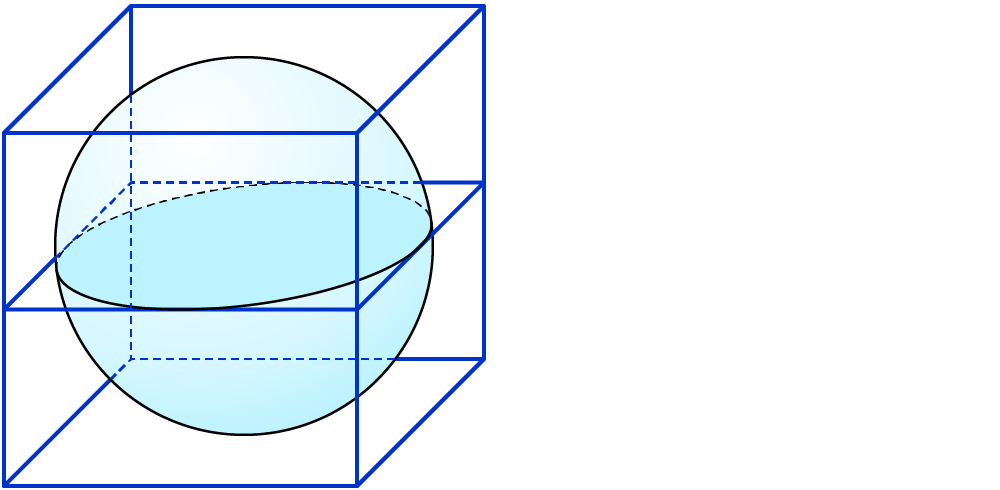
$$V_W = d^3$$

$$V_W = (8 \ cm)^3$$

$$V_W = 512 \ cm^3$$

Die Hälfte des Würfelvolumens sind $$256 $$ $$cm^3$$; $$268,08$$ $$ cm^3$$ sind ungefähr die Hälfte, du hast also richtig gerechnet.

Den Radius bei gegebenem Volumen berechnen

Gegeben ist eine Kugel mit einem Volumen von $$V = 855,63$$ $$cm^3$$.

Um den Radius der Kugel zu berechnen, gehe so vor:

1. Setze das gegebene Volumen in die Formel ein:

$$V = 4/3pi * r^3$$

$$855,63 $$ $$cm^3 =4/3pi * r^3$$

2. Löse die Formel nach $$r$$ auf:

$$855,63 $$ $$cm^3 =4/3pi * r^3$$  $$|*3/4$$ $$ |:pi$$

$$(855,63  cm^3*3)/(pi*4) = r^3$$   $$|root 3$$

$$root 3 ((855,63  cm^3*3)/(pi*4))=r$$

$$root 3 (204,27   cm^3)=r$$

$$5,89$$ $$cm$$ $$=$$ $$r$$

Du kannst auch erst die Formel nach r auflösen und dann das gegebene Volumen einsetzen:

$$V = 4/3pi * r^3$$  $$|*3/4$$ $$ |:pi$$

$$(V*3)/(pi*4) = r^3$$   $$|root 3$$

$$root 3 ((V*3)/(pi*4))=r$$

$$root 3 ((855,63  cm^3*3)/(pi*4))=r$$

$$root 3 (204,27   cm^3)=r$$

$$5,89$$ $$cm$$ $$=$$ $$r$$

Mit der Dichte rechnen

Für viele Aufgaben brauchst du die Dichte. Damit kannst du z. B. die Masse eines Körpers berechnen.

Die Dichte ist der Quotient Masse/Volumen. Mit Symbolen: $$rho = m/V$$. Die Einheit ist $$g/(cm^3)$$ oder $$(kg) /(m^3)$$.

Berechne die Masse einer Holzkugel mit $$4$$ $$cm$$ Durchmesser. Die Dichte von Holz beträgt etwa $$0,5 g/(cm^3)$$.

Berechne zuerst das Volumen:

$$r=2$$ $$cm$$

$$V = 4/3*pi * r^3 $$

$$V = 4/3*pi * (2  cm)^3$$

$$V ≈ 33,51$$ $$cm^3$$

Berechne die Masse:

$$rho = m/V$$ lässt sich umformen zu:

$$m=rho * V$$

$$m=0,5 g/(cm^3)*33,51 cm^3$$

$$m ≈ 16,76 \ g $$