Einleitung

Viele Anwendungen kannst du mithilfe des Satzes von Pythagoras berechnen.

Zeichne zuerst immer eine Skizze. Markiere den rechten Winkel und alle gegebenen Längen.
So siehst du auf den ersten Blick, welche Länge gesucht ist: eine Kathete oder die Hypotenuse.

Zur Erinnerung:

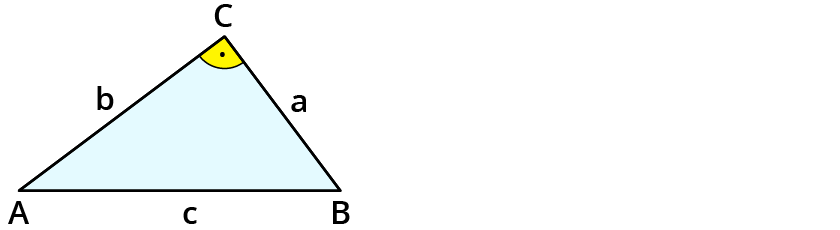
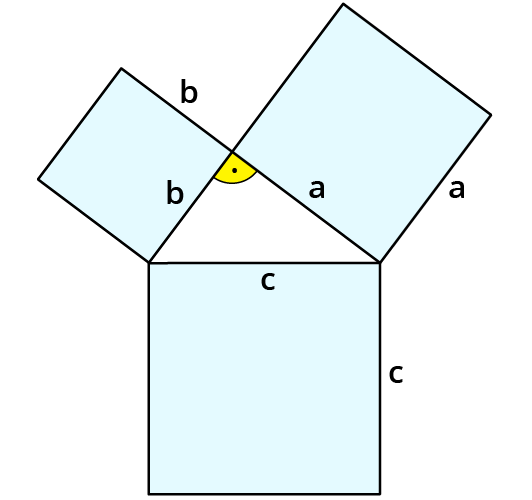
Der Satz des Pythagoras lautet

$$c^2 = a^2 + b^2$$,

wenn $$c$$ die Hypotenuse im rechtwinkligen Dreieck ist. $$a$$ und $$b$$ sind Katheten. Du rechnest mit dem Satz immer erst eine Fläche aus. Zu einer Länge gelangst du durch Wurzelziehen, z.B. $$c= sqrt (a^2 + b^2)$$.

Der Satz des Pythagoras lässt sich umstellen zu der Form

$$a^2 = c^2 - b^2$$

oder

$$b^2 = c^2 - a^2$$.

In jedem Fall wird von dem Hypotenusenquadrat das Kathetenquadrat abgezogen.

Die Leiter

Wie hoch reicht eine 4 m lange Leiter hinauf, wenn du sie 1,5 m entfernt von der Hauswand aufstellst?

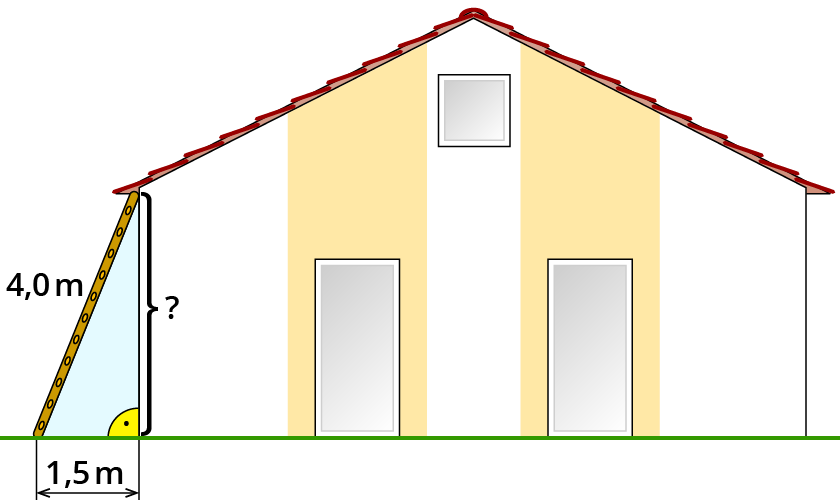
In dieser Aufgabe liegt ein rechtwinkliges Dreieck. Also kannst du den Satz von Pythagoras anwenden, um die fehlende Seite im Dreieck zu berechnen.

Skizze:

Du siehst, dass die Hypotenuse mit 4 m und eine Kathete mit 1,5 m gegeben sind.

Lösung:

$$a^2=c^2-b^2$$

$$a^2=4^2-1,5^2$$

$$a^2=16-2,25$$

$$a^2=13,75$$ $$|sqrt( )$$

$$a approx 3,7$$ $$m$$

Am Ende einer Anwendungsaufgabe kommt ein Antwortsatz.

Die Leiter reicht ca. 3,7 m an der Hauswand hinauf.

Das Spielfeld

Mathias läuft beim Training 10 x diagonal über das Feld mit den Maßen 100 m mal 50 m. Legt Mathias eine längere Strecke als 1 km zurück?

Skizze:

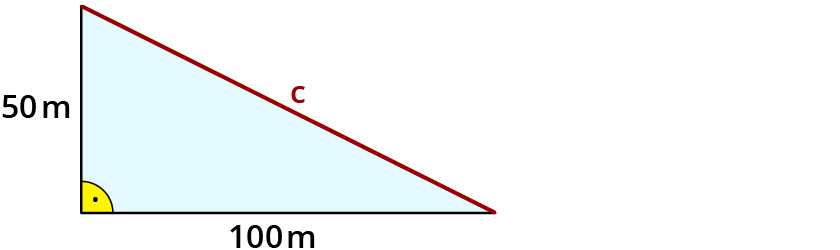
Du siehst, dass die Hypotenuse fehlt.

Lösung:

$$c^2=a^2+b^2$$

$$c^2=100^2+50^2$$

$$c^2=10000+2500$$

$$c^2=12500$$

$$c approx 111,8$$ $$m$$

Mathias läuft die Strecke 10 Mal.

$$111,8*10=1118$$ $$m$$

$$1$$ $$km$$ $$=1000$$ $$m$$

Antwortsatz: Mathias legt mehr als 1 km zurück.

Bild: iStockphoto.com (Jenny Hill)

Kombination von Aufgabentypen

Pythagorasaufgaben können auch mit anderen Feldern der Mathematik kombiniert werden.

Beispiel Trainingslauf

Der Trainer stellt frei, ob die Fußballer lieber 10 x diagonal über das Feld (50 m x 100 m) laufen wollen oder 4 x das Feld umrunden wollen. Um wie viel % ist der Diagonalenlauf (10 x) kürzer als die Feldumrundung (4 x)?

Lösung:

Diagonalenlauf:
$$111,8*10=1118$$ $$m$$

Umfang des Felds:
$$U_(Feld)=50+100+50+100=300$$ $$m$$

$$4$$ x Feldumrundung:
$$300*4=1200$$ $$m$$

$$rarr$$ Berechne den Prozentsatz: $$1118$$ $$m$$ von $$1200$$ $$m$$.

Prozentwert $$PW$$: $$1118$$ $$m$$

Grundwert $$GW$$: $$1200$$ $$m$$

Prozentsatz $$p$$: ?

$$p=(PW)/(GW) * 100 = 1118/1200 *100 approx 93,2 %$$

Der Weg entlang der Diagonalen ist $$6,8%$$ kürzer.