Exponentielles Wachstum
Wenn das Wachstum auch noch wächst
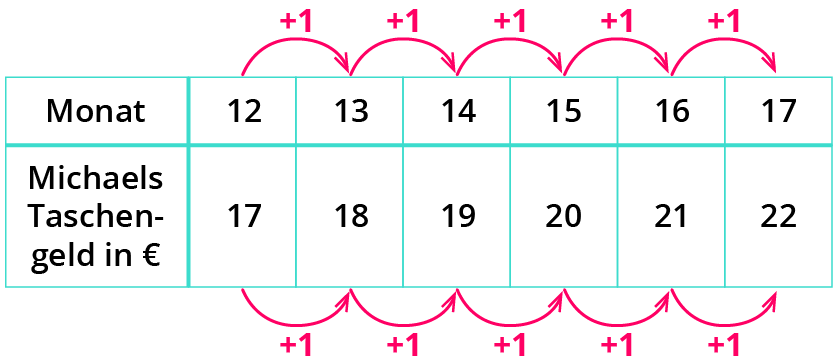
Michael und Peter sind Zwillinge und gerade 14 Jahre alt geworden. Es stehen die Verhandlungen für mehr Taschengeld an. Zur Zeit bekommen beide 5 €.
Michael schlägt seinem Vater vor, jeden Monat 1 € mehr zu bekommen. Peter hingegen möchte 10 % pro Monat mehr. Michael sagt: „Da habe ich immer mehr Geld als du, bis meine Ausbildung mit 16 beginnt.“ Peter sagt: „Du täuschst dich!“
Also wird gerechnet:
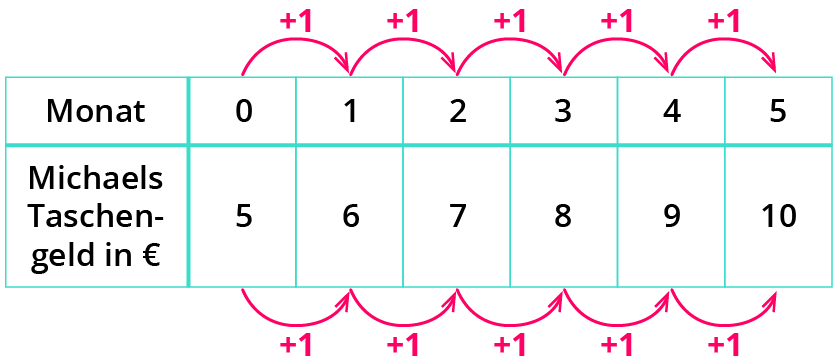
Michaels Taschengeld
Peters Taschengeld
Jeden Monat 10 % mehr heißt: 110 % des Vormonats. Kurz als Rechnung notiert: $$*$$1,1.
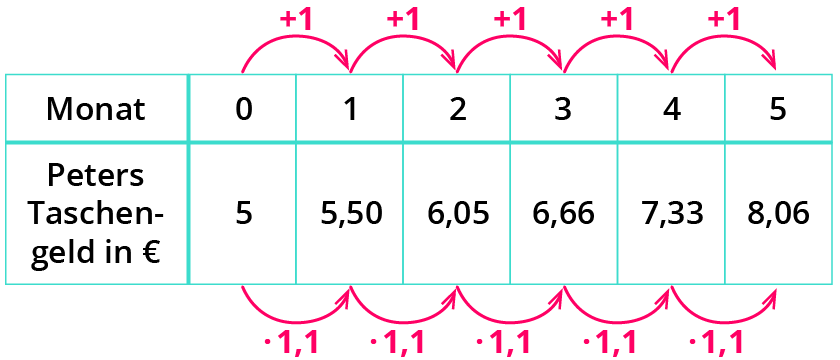
Tatsächlich scheint Michael recht zu behalten. Nach 5 Monaten hat er schließlich mehr Geld.
Ein Jahr später
Schon im zweiten Jahr ändert sich das Bild: Ab dem 14. Monat hat Peter mehr Geld als Michael. Und der Abstand zwischen Michaels und Peters Geldbetrag wird größer!
Michaels Taschengeld
Peters Taschengeld
Peters Taschengeld wächst schneller. Es wächst exponentiell!
Ein Wachstum, bei dem jeder Funktionswert durch Multiplikation des vorhergehenden Funktionswertes mit einem festen Faktor entsteht, heißt exponentielles Wachstum.
Wachstum mathematisch
Mathematiker hantieren ja gern mit x und y. Du ordnest den x Werten (Monaten) y-Werte (Taschengeld) zu.
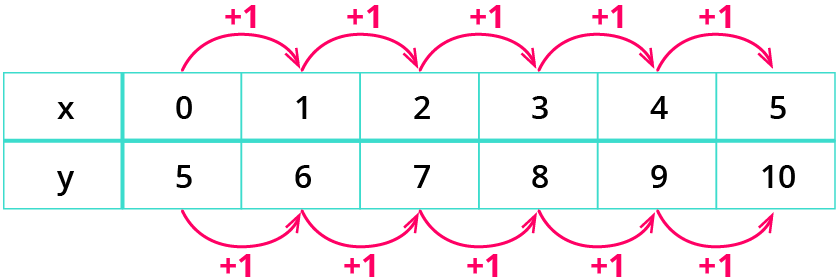
Michael bekommt von Monat zu Monat immer einen 1 € mehr. Die Wachstumsrate (Änderungsrate) bleibt gleich: 1 €. Das ist lineares Wachstum.
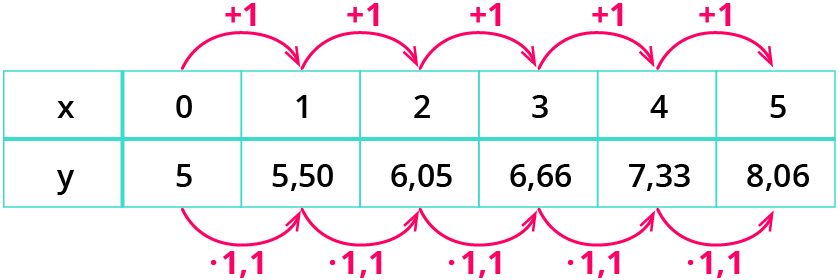
Die Änderungsrate von Peters Taschengeld verändert sich:
zu Beginn: 5,50 € $$-$$ 5 € $$=$$ 0,50 €
6,05 € $$-$$ 5,50 € $$=$$ 0,55 €
später:
19,10 € $$-$$ 17,40 € $$=$$ 1,70 €,
21 € $$-$$ 19,10 € $$=$$ 1,90 €
Michaels Taschengeld wächst viel schneller und sogar immer schneller. Die Wachstumsrate (Änderungsrate) steigt! Das ist so bei exponentiellem Wachstum.
Wieso heißt das „exponentielles Wachstum“?
Peters Taschengeld kannst du auch mit Potenzen berechnen, denn statt jeweils den Vorgänger mit 1,1 zu multiplizieren, geht es auch wie in der Tabelle:
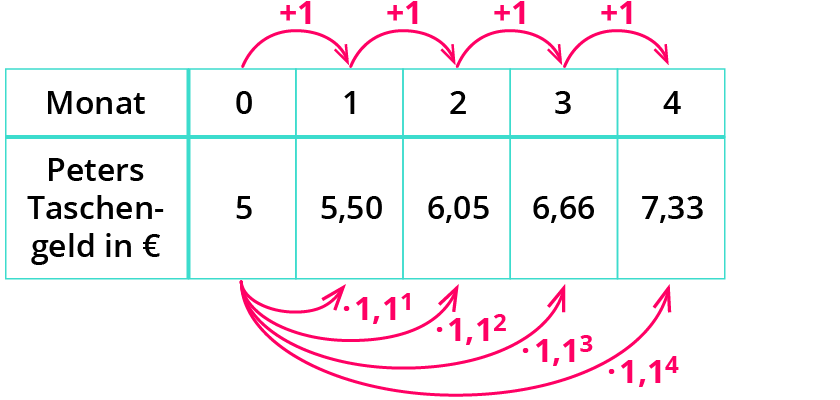
Der Exponent ist veränderlich: In den Exponenten setzt du die x-Werte ein.
Unter einer Änderungsrate versteht man die Menge, die zwischen zwei Zeiteinheiten oder Argumenten einer Funktion hinzukommt.
Exponentielles Wachstum genauer betrachtet
Betrachtest du noch einmal das Beispiel von Peter und Michael, so kannst du die Wachstumsraten und Graphen gegenüberstellen.
Lineares Wachstum
(Michaels Taschengeld)
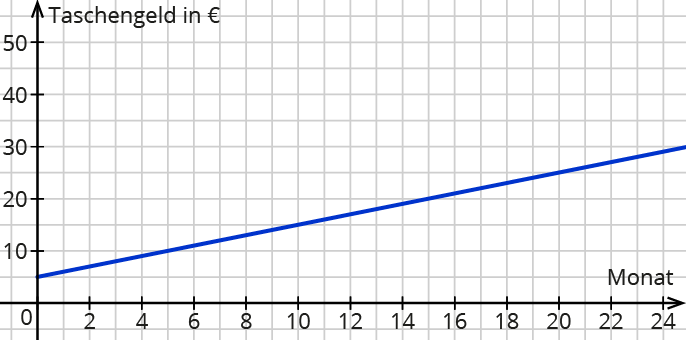
Der Graph ist eine Gerade mit y-Achsenschnittpunkt beim Startwert.
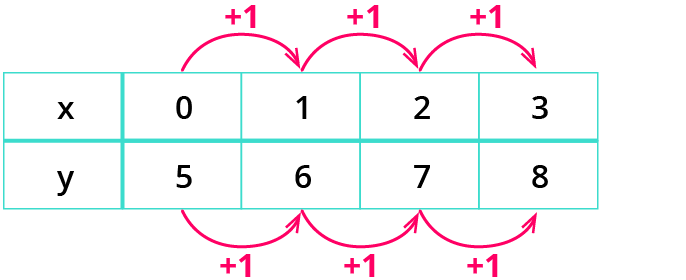Die Funktionswerte wachsen immer mit konstantem Summanden von +1.
Die Änderungsrate bleibt gleich.
Die Funktionsgleichung lautet $$f(x)=x+5$$.
Lineares Wachstum kannst du durch eine Funktion der Form $$f(x)=m*x+b$$ beschreiben.
Exponentielles Wachstum
(Peters Taschengeld)
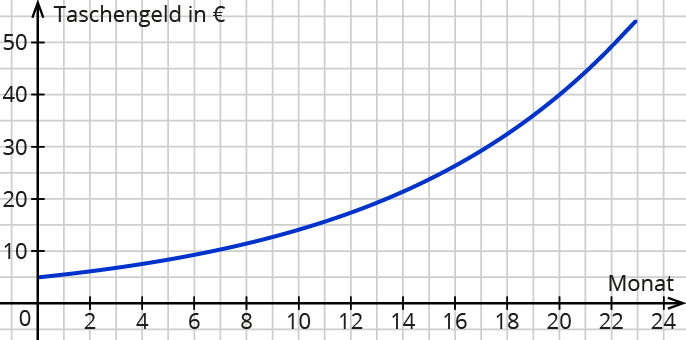
Der Graph verläuft stetig wachsend mit y-Achsenschnittpunkt beim Startwert.
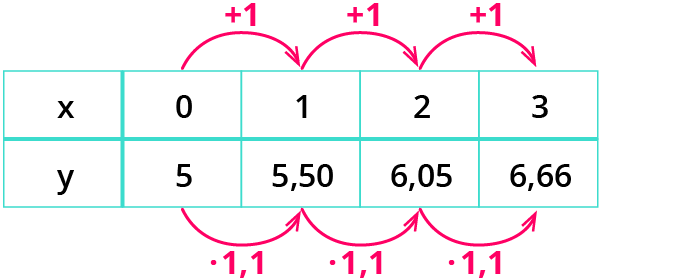Die Funktionswerte wachsen immer mit konstantem Faktor 1,1.
Die Änderungsrate nimmt zu. Sie beträgt erst 0,50€. dann 0,55 € dann 0,605 €.
Auch die Änderungsrate wächst mit dem Faktor 1,1.
Die Funktionsgleichung lautet $$f(x)=5 cdot 1,1^x$$.
Exponentielles Wachstum kannst du durch eine Funktion der Form $$f(x)=a*b^x$$ beschreiben.
$$b>0$$ und $$b != 1$$
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Wer behält recht?
Was bekommen Peter und Michael, wenn sie ihre Ausbildung beginnen?
Mit 16 Jahren werden die Brüder ihre Ausbildung beginnen. Das sind noch 24 Monate.
Wenn du die Funktionsgleichungen hast, kannst du ganz einfach das Taschengeld für beliebige Monate berechnen. Setze die Anzahl der Monate für x ein.
Michaels Taschengeld
Die Funktionsgleichung: $$f(x)=5€+x*1€$$
Der Wert, den du ausrechnest, heißt Funktionswert:
$$f(24)=5€+24*1€=29$$ $$€$$
Nach 24 Monaten erhält Michael also 29 €.
Peters Taschengeld
Die Funktionsgleichung: $$f(x)=5€*1,1^x$$.
Nach 24 Monaten bekommt er also:
$$f(24)=5€*1,1^24 =49,25$$ $$€$$
Peter bekommt also rund 20 € mehr.
Das stete Wachstum füllt das Konto.
Oma Greta hat für jeden ihrer Enkel ein Konto angelegt mit einem Startkapital von 1000 €. Auf das Konto werden 2 % Zinsen gezahlt, die Zinsen werden nicht abgehoben. Wenn die Enkel 18 sind, wird das Geld ausgezahlt. Wie viel Geld ist nach 18 Jahren auf dem Konto?
Vielleicht Kommt dir das bekannt vor? Du berechnest hier die Zinsen von den Zinsen, also die Zinseszinsen. Dazu brauchst du den Zinsfaktor: Bei 2 % Zinsen ist der Zinsfaktor 1,02.
So geht’s:
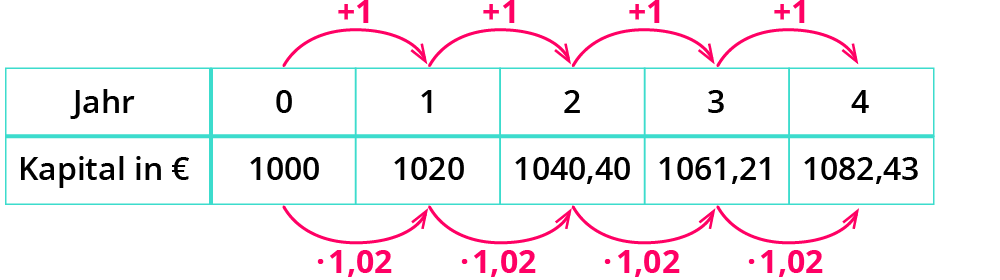
Zur Berechnung eines jeden Tabelleneintrages wird der vorangegangene Eintrag mit 1,02 multipliziert.
Werden auch Zinsen auf das schon verzinste Guthaben gezahlt, spricht man von Zinseszins. Für die Berechnung addiert man die 2 % Zinsen zu den 100 % des Kapitals. Somit errechnet man 102% des vorangegangenen Wertes. 102 % kannst du mit dem Zinsfaktor 1,02 berechnen.
Schritt für Schritt oder gleich das Ergebnis
Kemal ist Gretas Enkel und er möchte errechnen, wie viel Geld er am Ende auf dem Konto hat.
| Jahr | 1 | 2 | 3 |
| Kapital in € | 1020 | 1040,40 | 1061,21 |
Für die Tabelleneinträge stellt er folgende Rechnungen auf:
Nach einem Jahr bekommt er: $$1000€ cdot 1,02=1020 €$$
Nach zwei Jahren bekommt er: $$1020€ cdot 1,02=1040,40€$$
Ihm fällt auf, dass er für das zweite Jahr auch mit dem Startwert hätte rechnen können.
$$1000€ cdot 1,02 cdot 1,02 =1040,40€$$
Oder noch kürzer: $$1000€ cdot 1,02^2=1040,40 €$$
So wird die Rechnung ganz einfach:
| Nach einem Jahr: | $$ 1000 € cdot 1,02 =1020€$$ |
| Nach 2 Jahren: | $$1000 € cdot 1,02^2=1040,40 €$$ |
| Nach 3 Jahren: | $$1000 € cdot 1,02^3=1061,21 €$$ |
| … | … |
| Nach 18 Jahren: | $$1000 € cdot 1,02^18=1428,25 €$$ |
Das Kapitel mit Zinseszinsen nach $$n$$ Jahren mit Zinssatz p und Startkapitel $$K$$ berechnest du so: $$K(n)=K cdot q^n$$
($$q$$ ist der Zinsfaktor $$q=1+p/100$$.)
Das Kapitel mit Zinseszinsen wächst also auch exponentiell. Die Veränderliche (hier n) steht im Exponenten.
Multiplizierst du gleiche Faktoren, kannst das als Potenz schreiben: $$a cdot a cdot a cdot a =a^4$$
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Eigenschaften von exponentiellem Wachstum
Innerhalb der letzten Kapitel hast du die Wachstums- und Abnahmeprozesse kennengelernt.
| Name | lineares Wachstum | exponentielles Wachstum |
|---|---|---|
| Eigenschaft | Zahlenwerte ändern sich proportional zum Argument | Zahlenwerte ändern sich immer mit dem selben Faktor zum vorigen Wert |
| Funktions- gleichung | $$f(x)=m*x+n$$ | $$f(x)=a*b^x$$ $$a!=0;b >1$$ |
| Änderungsrate | fest | ändert sich |
| Berechnung | Zur Berechnung des nachfolgenden Funktionswertes wird immer die selbe Zahl zum Funktionswert hinzuaddiert. | Zur Berechnung des nachfolgenden Funktionswertes wird immer die selbe Zahl mit dem Funktionswert multipliziert |
| Funktions- graph | Gerade | Graph einer exponentiellen Funktion |
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
