Mit der bedingten Wahrscheinlichkeit rechnen
Zum Festival
Aus allen Kandidaten der Sek I und Sek II eines Gymnasiums für die Teilnahme an einem Festival soll ein Kandidat ausgewählt werden. Die Daten für die Wahl sind in einer Vierfeldertafel dargestellt.
Ereignis $$A$$: Sek I, Ereignis $$barA$$: Sek II,
Ereignis $$B$$: Mädchen, Ereignis $$barB$$: Junge
Das sind die Anzahlen für die einzelnen Kandidaten:
| $$B$$ | $$barB$$ | Summe | |
|---|---|---|---|
| $$A$$ | |||
| $$barA$$ | |||
| Summe |
Wie groß sind die Wahrscheinlichkeiten für die Ereignisse?
| $$B$$ | $$barB$$ | Summe | |
|---|---|---|---|
| $$A$$ | |||
| $$barA$$ | |||
| Summe |
Im Baumdiagramm sieht das so aus:
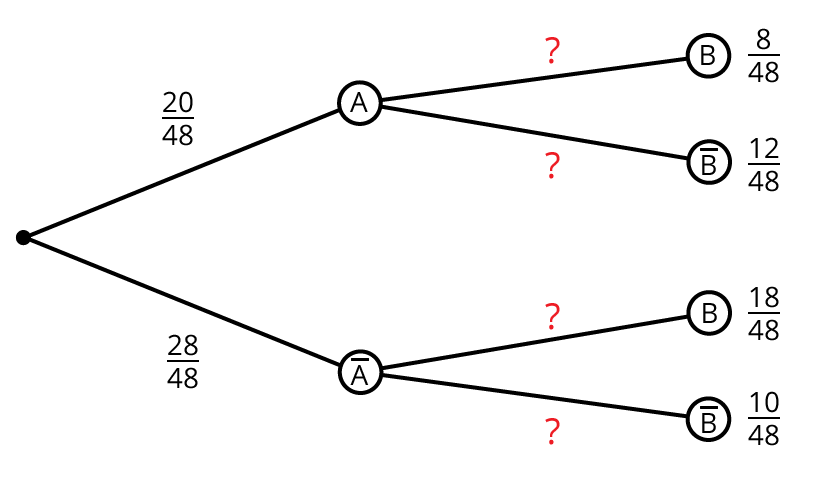
Und was ist mit den Wahrscheinlichkeiten in der Mitte? Klar, die kannst du berechnen.
Zum Beispiel die Wahrscheinlichkeit, dass ein Mädchen ausgewählt wird, mit der Voraussetzung, dass es in der Sek I ist. Das sind bedingte Wahrscheinlichkeiten.
Sek I ist die Sekundarstufe 1 (Klassen 5 bis 9 oder 10). Sek II ist die Sekundarstufe 2 (Oberstufe).

Bild: alamy images (Adrian Sherratt)
Das hier ist in England: das „Cheltenham Literature Festival“.
Zuerst die Theorie: Bedingte Wahrscheinlichkeiten
Das Baumdiagramm markiert ein Zufallsexperiment, bei dem das Ereignis B eintritt, nachdem das Ereignis A eingetreten ist.
Die Bezeichnung ist $$P(B|A)$$: Die Wahrscheinlichkeit von B unter der Bedingung, dass A eingetreten ist. Oder kurz: Die Wahrscheinlichkeit von B unter der Bedingung A.
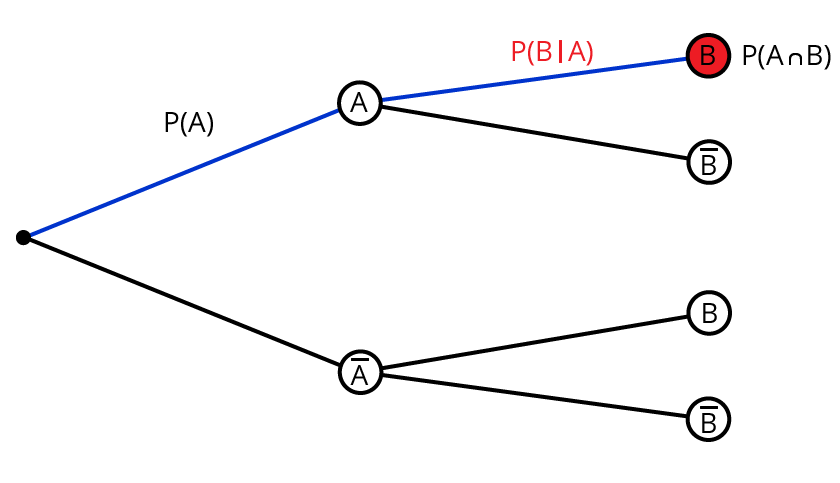
Erinnerst du dich an die erste Pfadregel für Baumdiagramme?
Hier gilt: $$ P(A) * P(B|A) = P(AcapB)$$
(mit $$ P(A) > 0$$).
Wenn du die Gleichung umstellst, hast du eine Gleichung, mit der du die bedingte Wahrscheinlichkeit berechnen kannst.
Für die bedingte Wahrscheinlichkeit gilt:
$$P(B|A) = frac{P(AcapB)}{ P(A)}, P(A) > 0$$
Eine andere Schreibweise für die bedingte Wahrscheinlichkeit ist $$P_A(B)$$.
Eine weitere Sprechweise ist: $$P(B|A)$$ ist die durch A bedingte Wahrscheinlichkeit von B.
Zurück zum Festival
Hier noch mal die Festival-Kandidaten:
Ereignis $$A$$: Sek I, Ereignis $$barA$$: Sek II
Ereignis $$B$$: Mädchen, Ereignis $$barB$$: Junge
| $$B$$ | $$barB$$ | Summe | |
|---|---|---|---|
| $$A$$ | |||
| $$barA$$ | |||
| Summe |
Nach der Wahl sickert durch, dass ein Mädchen gewählt wurde. Kurz darauf plaudert ein Mitglied der Wahlkommission aus, dass die Kandidatin aus der Sek II stammt.
Das ist der Pfad im Baumdiagramm:
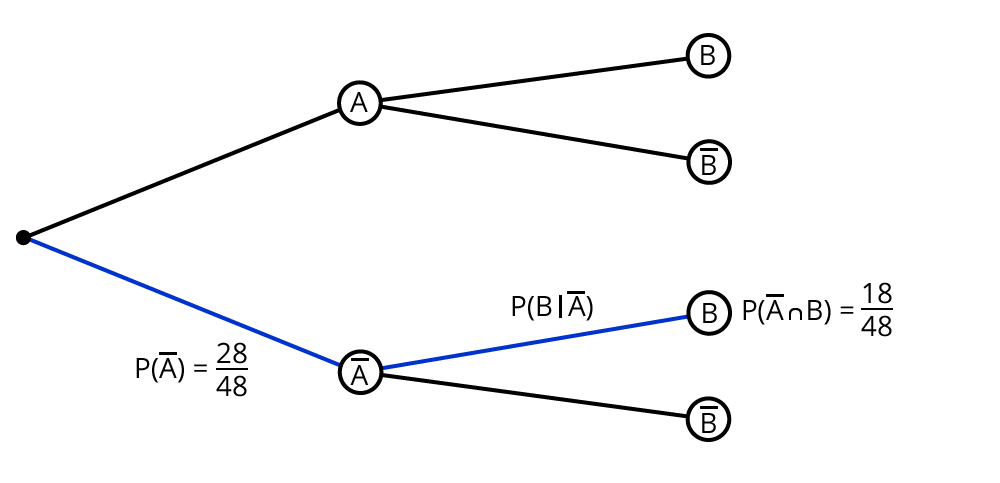
Die Wahrscheinlichkeit, dass der Kandidat ein Mädchen ist ($$B$$) unter der Bedingung, dass es aus der Sek II kommt ($$bar A$$), berechnest du so:
$$P(B|bar A) = frac{P(barAcapB)}{ P(barA)} = frac{18/48}{ 28/48}=18/28$$
Ohne die Zusatzinformation „Kandidat aus der Sek II“ gibt es 26 günstige und 48 mögliche Fälle, während es mit Zusatzinformation nun 18 günstige und nur noch 28 mögliche Fälle gibt.
Benutze diese Schreibweisen:
$$P(AcapB)$$ ist die Wahrscheinlichkeit von $$A$$ und $$B$$.
$$P(B|A) $$ ist die Wahrscheinlichkeit von $$B$$ unter der Bedingung $$A$$.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Umkehrung von Baumdiagrammen
Macht es eigentlich einen Unterschied, welche Merkmale (Merkmale $$A , barA$$ oder $$B, barB$$ ) du „zuerst“ nimmst?
Probier’s aus:
Gegeben ist diese Vierfeldertafel:
| $$B$$ | $$barB$$ | Summe | |
|---|---|---|---|
| $$A$$ | |||
| $$barA$$ | |||
| Summe |
Das Baumdiagramm:
Und umgekehrt
| $$A$$ | $$barA$$ | Summe | |
|---|---|---|---|
| $$B$$ | |||
| $$barB$$ | |||
| Summe |
Das Baumdiagramm:
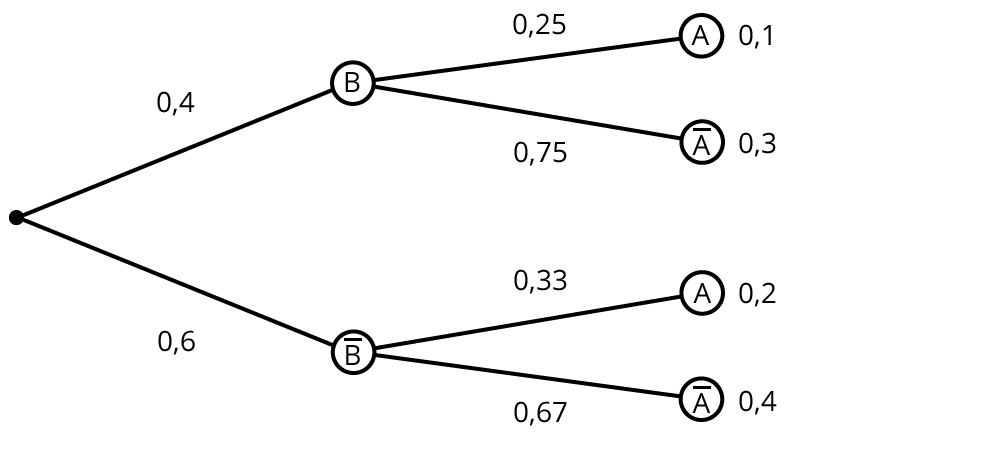
Das Vertauschen der Merkmale $$A ,barA$$ und $$B, barB$$ bei einem Baumdiagramm führt zu einander umgekehrten Baumdiagrammen.
Du siehst, dass sich die an den einzelnen Pfaden stehenden Wahrscheinlichkeiten im Allgemeinen unterscheiden. Dies ist darauf zurückzuführen, dass sie sich auf verschiedene Merkmale und damit auf verschiedene Teilgesamtheiten beziehen.
Da sich die Wahrscheinlichkeiten am Pfadende auf dieselbe Vierfeldertafel beziehen, stimmen sie bis auf die Reihenfolge überein.
Bedingte Wahrscheinlichkeiten verwendest du nicht nur, um von einer Bedingung oder Ursache $$A$$ auf eine Wirkung $$B$$ zu schließen, sondern auch, um mittels einer Wirkung $$B$$ auf eine Ursache $$A$$ zu schließen.
Beide Wahrscheinlichkeiten, $$P(A)$$ und $$P(B|A)$$, kannst du mit einem Baumdiagramm bzw. seiner Umkehrung berechnen.
Festival mit Umkehrung
Wie ist das mit der Umkehrung bei der Festival-Aufgabe?
Ereignis $$A$$: Sek I, Ereignis $$barA$$: Sek II
Ereignis $$B$$: Mädchen, Ereignis $$barB$$: Junge
| $$B$$ | $$barB$$ | Summe | |
|---|---|---|---|
| $$A$$ | |||
| $$barA$$ | |||
| Summe |
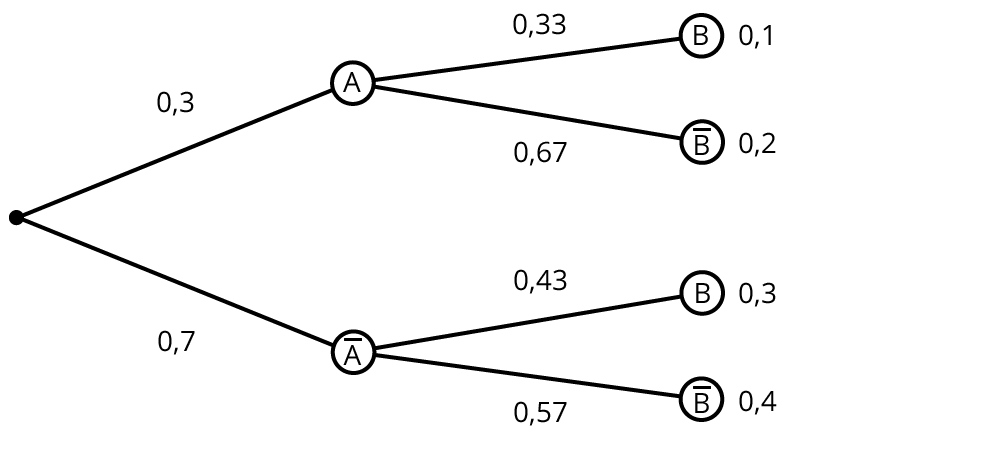
Folgende Wahrscheinlichkeiten kannst du ablesen:
- Die Wahl fällt auf einen Kandidaten aus der Sek II: $$P(barA) = frac {28}{48}$$
- Die Wahl fällt auf ein Mädchen: $$P(B) = frac {26}{48}$$
- Die Wahl fällt auf ein Mädchen aus der Sek II: $$P(barA cap B) = frac {18}{48}$$
Veränderte Bedingung
Nun wird zuerst bekannt, dass der Kandidat aus der Sek II stammt und dann, dass es ein Mädchen ist.
Du berechnest also die bedingte Wahrscheinlichkeit $$P(B|bar A)$$.
Hier ist das umgekehrte Baumdiagramm:
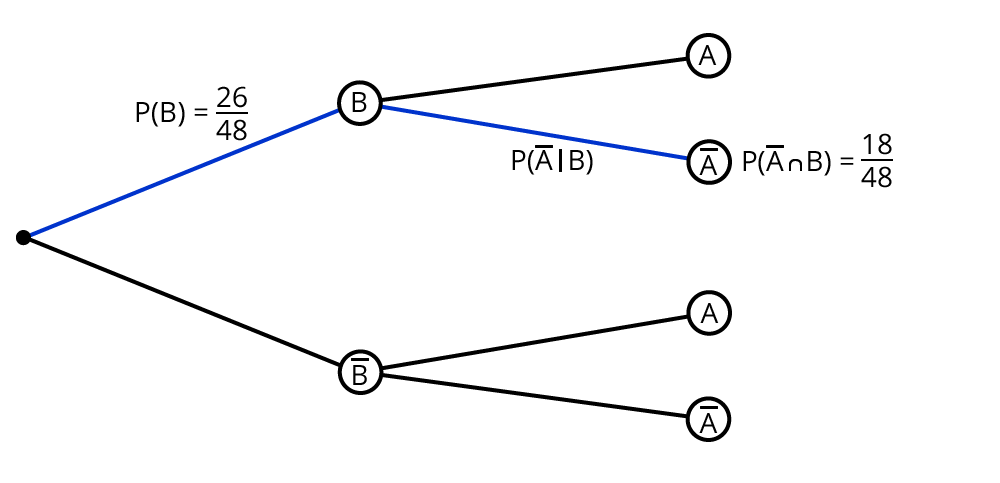
Die Wahrscheinlichkeit, dass der Kandidat aus der Sek II stammt ($$barA$$), unter der Bedingung, dass es ein Mädchen ist ($$B$$), berechnest du so:
$$P(barA|B) = frac{P(barAcapB)}{ P(B)} = frac{18/48}{ 26/48}=18/26$$.
Allgemein gilt für die bedingte Wahrscheinlichkeit:
$$P(B|A) = frac{P(AcapB)}{ P(A)}$$ und umgekehrt $$P(A|B) = frac{P(AcapB)}{ P(B)}$$ .
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



