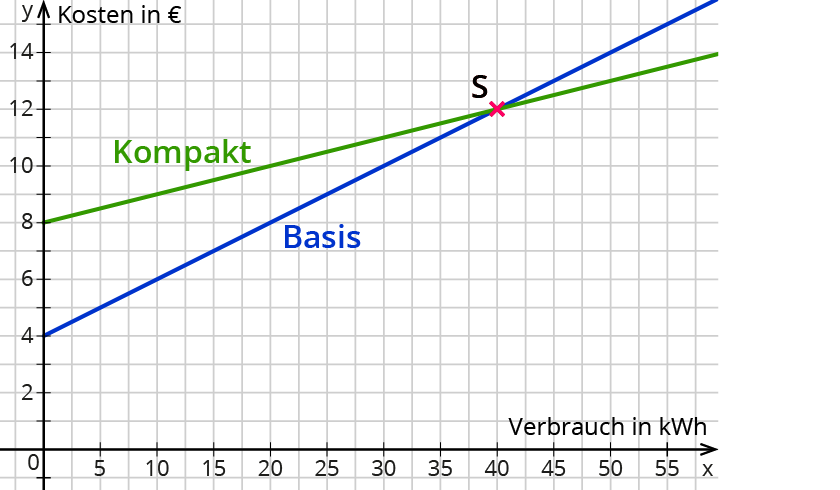
Gleichungssysteme mit leerer Lösungsmenge oder mit unendlich vielen Lösungen lösen
Die Lösungsmenge von linearen Gleichungssystemen
Für die Art der Lösungsmenge eines linearen Gleichungssystems gibt es drei Möglichkeiten:
genau eine Lösung
Beispiel: $$L={(2|3)}$$keine Lösung
Man sagt auch die Lösungsmenge ist leer.unendlich viele Lösungen
Hier lernst du die Fälle $$2$$ und $$3$$ kennen.
Fall 2: Lineare Gleichungssysteme mit leerer Lösungsmenge
Hat ein lineares Gleichungssystem keine Lösung, verlaufen die Graphen parallel zueinander.
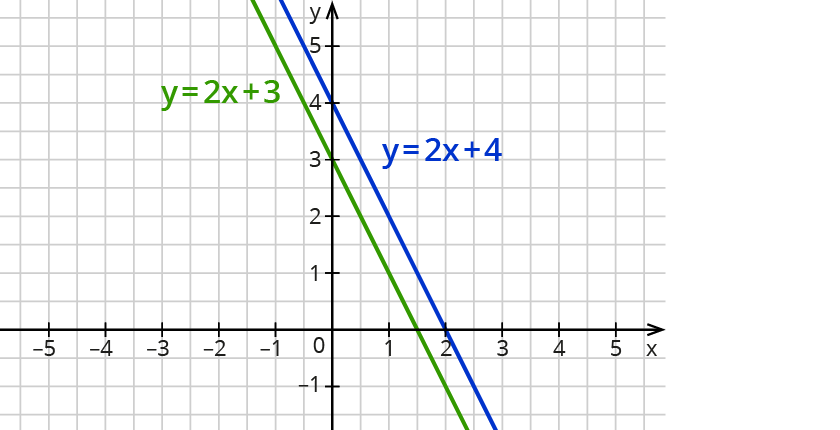
So stellst du rechnerisch fest, dass ein lineares Gleichungssystem keine Lösung hat:
$$I$$ $$10x+5y=15$$ $$|*2$$
$$II$$ $$-4x-2y=-8$$ $$|*5$$
$$I$$ $$20x+10y=30$$
$$II$$ $$-20x-10y=-40$$
$$I+II$$ $$0=-10$$
Die letzte Gleichung ist eine falsche Aussage. Du kannst daher kein Zahlenpaar ($$x|y$$) finden, das beide Gleichungen $$I$$ und $$II$$ erfüllt. Die Lösungsmenge ist also leer: $$L={$$ $$}$$
Du kannst selbst entscheiden, mit welchem Verfahren du die Lösungsmenge berechnest.
Für die leere Lösungsmenge $$L={}$$ ist auch diese Schreibweis möglich: $$L=O/$$.
Fall 3: Lineare Gleichungssysteme mit unendlich vielen Lösungen
Hat ein lineares Gleichungssystem unendlich viele Lösungen, so sind die Graphen identisch.
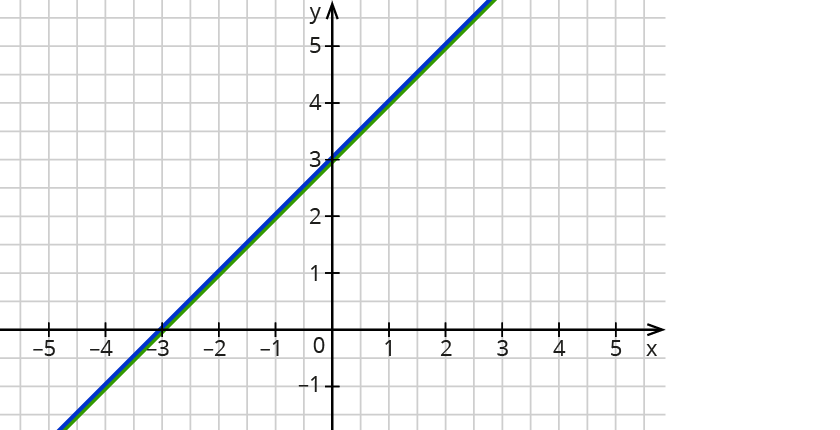
So stellst du rechnerisch fest, dass ein lineares Gleichungssystem unendlich viele Lösungen hat:
$$I$$ $$-2x+2y=6$$ $$|*3$$
$$II$$ $$3x-3y=-9$$ $$|*2$$
$$I$$ $$-6x+6y=18$$
$$II$$ $$6x-6y=-18$$
$$I+II$$ $$0=0$$
Die letzte Gleichung ist eine wahre Aussage. Daher löst jedes Zahlenpaar $$(x|y)$$, das eine der beiden Gleichungen erfüllt, das Gleichungssystem.
Stelle zur Angabe der Lösungsmenge eine der beiden Gleichungen nach $$y$$ um.
$$-2x+2y=6$$ $$|+2x$$ oder $$3x-3y=-9$$ $$|-3x$$
$$2y=2x+6$$ $$|:2$$ $$-3y=-3x-9$$ $$|$$ $$:$$$$(-3)$$
$$y=x+3$$ $$y=x+3$$
Die Lösungsmenge lautet: $$L={(x|y)$$ $$|$$ $$y=x+3}$$
Gesprochen heißt es: Die Lösungsmenge besteht aus den Zahlenpaaren $$(x|y) $$ für die gilt: $$y=x+3$$
Zahlenpaare, die das Gleichungssystem erfüllen, sind zum Beispiel: $$x=1$$ und $$y=1+3=4$$ also $$(1|4)$$
oder
$$x=3$$ und $$y=3+3=6$$ also $$(3|6)$$

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen