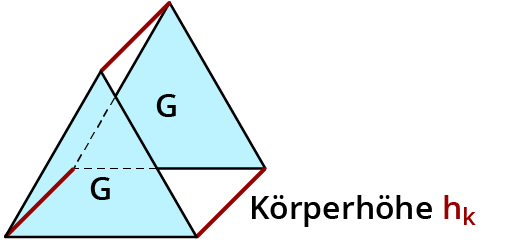
Zylinder untersuchen
Was ist ein Zylinder?
Ein Zylinder ist ein Körper. Dieser hat wie andere Prismen zwei Grundflächen und eine Mantelfläche. Beim Zylinder sind die Grundflächen Kreise.
Die Mantelfläche besteht aus einem Rechteck. Der Abstand zwischen den Grundflächen ist die Körperhöhe $$h_k$$.

Bild: stock.adobe.com/Willman, Dave
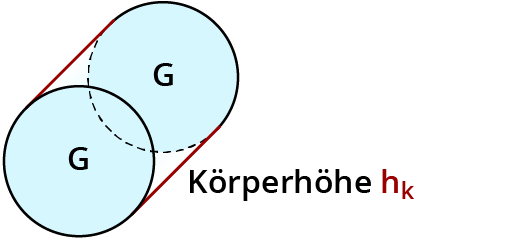 Grundfläche vorne und hinten
Grundfläche vorne und hinten
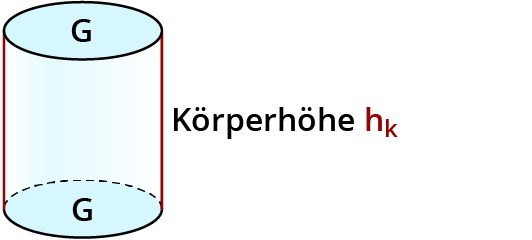 Grundfläche oben und unten
Grundfläche oben und unten
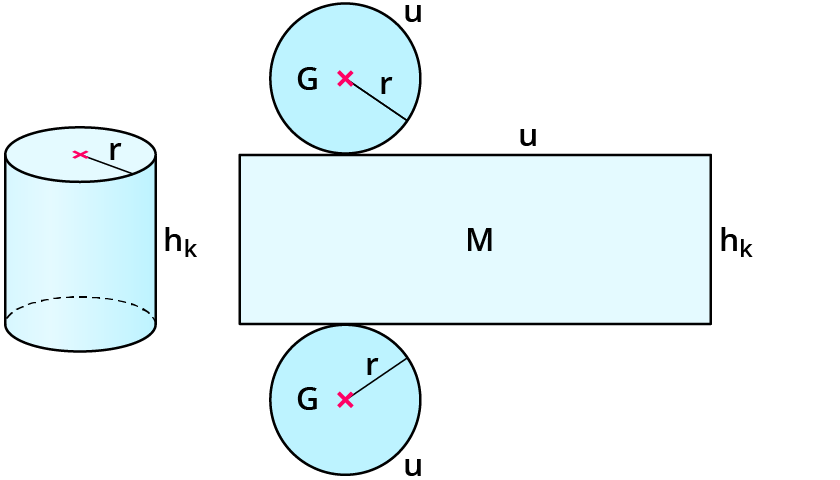
Das Netz eines Zylinders
Wenn du den Zylinder zu einem Netz ausklappt, kannst du alle äußeren Flächen gut erkennen:
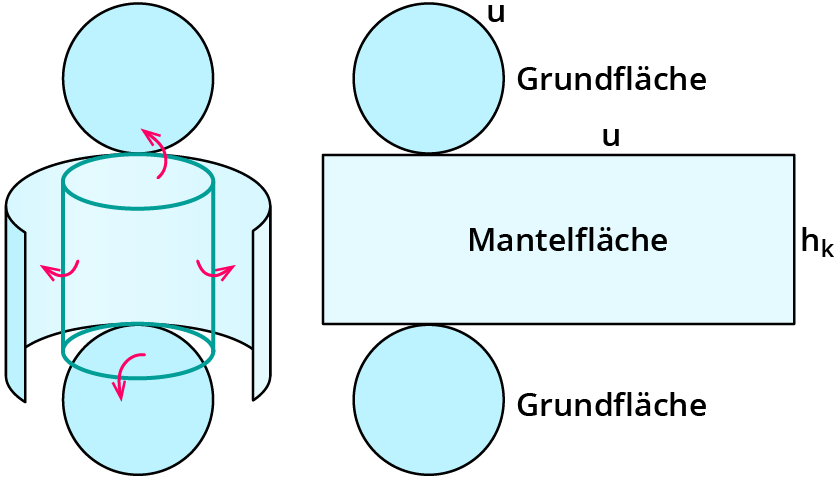
Du siehst die Mantelfläche und zweimal die Grundfläche. Man nennt diese äußeren Flächen des Zylinders seine Oberfläche.
Wenn du das Netz eines Zylinders zeichnest, ist es am übersichtlichsten, wenn du die Grundflächen oben und unten von der Mantelfläche zeichnest. Alle Flächen behalten dabei ihre Originalgröße. Die Mantelfläche hat die Seitenlängen: Umfang u des Kreises sowie die Körperhöhe $$h_k$$.
Die äußeren Flächen sind die Flächen, die du berühren kannst, wenn du den Zylinder in der Hand hältst.
Oberfläche eines Zylinders berechnen
Gegeben ist ein Zylinder mit den Längen $$r = 5,8\ cm$$, $$h_k = 5\ cm$$.
So berechnest du den Oberflächeninhalt eines Zylinders:
- Berechne die Grundfläche.
- Berechne die Mantelfläche.
- Berechne: Oberfläche $$= 2 *$$ Grundfläche $$+$$ Mantelfläche Kurzschreibweise: $$O = 2 * G + M$$
Beispiel

Um die Oberfläche zu berechnen, gehe so vor:
1. Berechne die Grundfläche.
$$G = π * r^2$$
$$G = π * (5,8\ cm)^2$$
$$G approx 105,68\ cm^2$$
2. Berechne die Mantelfläche.
Sie hat die Seitenlängen: Körperhöhe des Prismas $$h_k$$ und Umfang $$u$$ des Kreises.
Umfang des Kreises:
$$u = 2 * π * r$$
$$u = 2 * π * 5,8\ cm$$
$$u = 36,44\ cm$$
Mantelfläche:
$$M = u* h_k$$
$$M =36,44\ cm * 5\ cm$$
$$M = 182,2\ cm^2$$
3. Berechne die Oberfläche:
Oberfläche $$= 2 *$$ Grundfläche $$+$$ Mantelfläche
$$O = 2 * G + M$$
$$O = 2 * 105,68\ cm^2 + 182,2\ cm^2$$
$$O = 211,36\ cm^2 + 182,2\ cm^2$$
$$O = 393,56\ cm^2$$
Flächeninhalt eines Kreises:
$$G = π * r^2$$

- $$π$$ Kreiszahl
- r Radius
Umfang eines Kreises:
$$u = 2 * π * r$$
oder: $$u = π * d$$
weil: $$2 * r = d$$
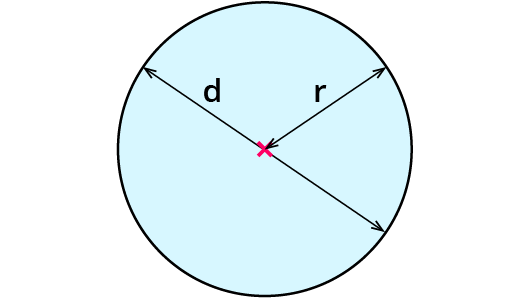
- $$d$$ Durchmesser
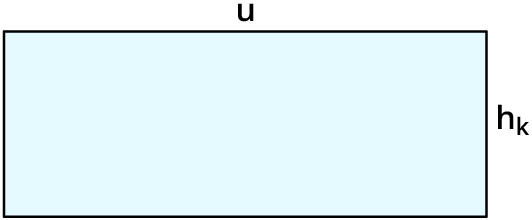
Flächeninhalt eines Rechtecks:
$$A=u*h_k$$
Das Schrägbild eines Zylinders
So zeichnest du ein Schrägbild:
Liegender Zylinder

1. Grundfläche in Originalgröße zeichnen
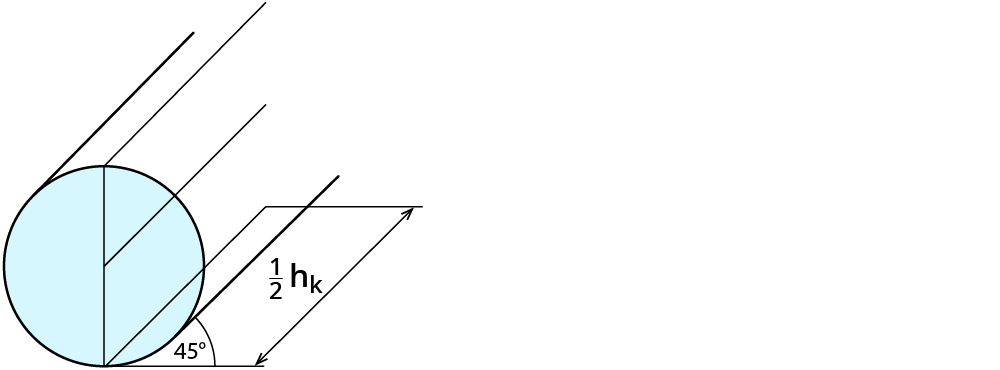
2. Senkrecht nach hinten laufende Kanten (Körperhöhe $$h_k$$) in halber Länge unter 45° zeichnen
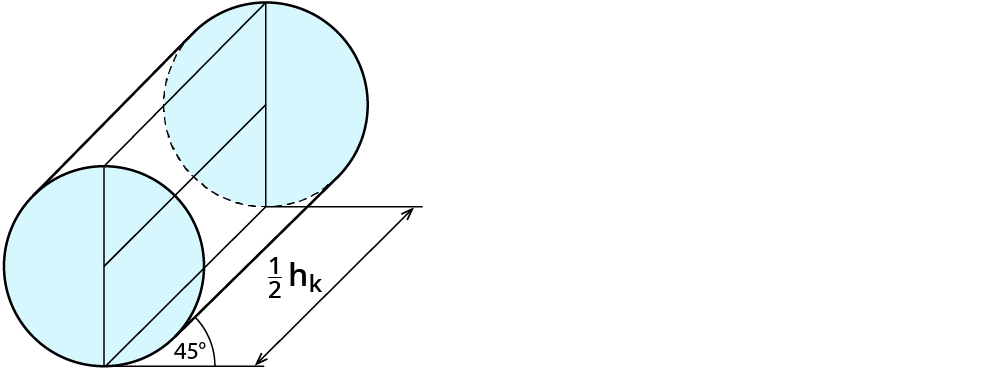
3. Die zweite Grundfläche ergänzen.
Das Schrägbild eines Zylinders
Stehender Zylinder

1. Die Grundfläche zeichnen: den waagerechten Durchmesser $$d$$ des Kreises in Originalgröße, den senkrechten Durchmesser in halber Länge zeichnen ($$d/2$$).

2. Die Körperhöhe $$h_k$$ in Originallänge im rechten Winkel zum waagerechten Durchmesser zeichnen.

3. Die zweite Grundfläche ergänzen.
Volumen eines Zylinders berechnen
Gegeben ist ein Zylinder mit den Längen $$r = 5,8\ cm$$, $$h_k = 5\ cm$$.

So berechnest du das Volumen eines Zylinders:
- Berechne die Grundfläche.
- Berechne das Volumen.
Volumen $$=$$ Grundfläche $$*$$ Körperhöhe
Kurzschreibweise: $$V = G * h_k$$
Um das Volumen zu berechnen, gehe so vor:
1. Berechne die Grundfläche.
$$G = π * r^2$$
$$G = π * (5,8\ cm)^2$$
$$G = π * 33,64\ cm^2$$
$$G = 105,68\ cm^2$$
2. Berechne das Volumen:
Volumen $$=$$ Grundfläche $$*$$ Körperhöhe.
$$V = G * h_k$$
$$V = 105,68\ cm^2 * 5\ cm$$
$$V = 528,4\ cm^3$$
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen