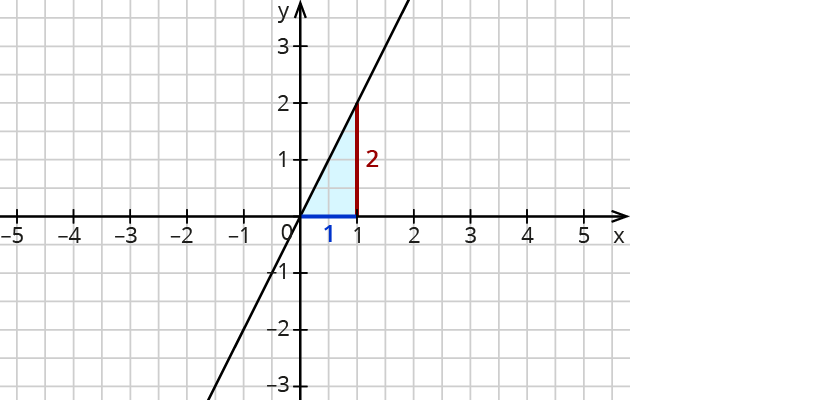
Proportionale Funktionen beschreiben
Proportionale Funktionen
Eine Zuordnung mit der Funktionsgleichung $$f(x)=mx$$ ist eine proportionale Funktion.
m ist dabei der Proportionalitätsfaktor.
Der Graph einer proportionalen Funktion ist eine Gerade durch den Koordinatenursprung.
Die Definitionsmenge einer proportionalen Funktion sind die Rationalen Zahlen $$QQ$$.
Zuordnungen, bei denen die Verdoppelung des Ausgangswerts („doppelt so viele Eier“) auch zu einer Verdoppelung des zugeordneten Werts („doppelt so viele €“) führt, heißen proportionale Zuordnungen oder Funktionen.
Rationale Zahlen sind positive und negative Brüche.
Wertetabellen zu proportionalen Funktionen erstellen
Lege für die Funktion $$f(x)=2x$$ eine aussagekräftige Wertetabelle an.
So gehst du vor:
- Schritt:
Überlege dir für welche x-Werte du eine Wertetabelle aufstellen sollst. Ist nichts vorgegeben, so nehme ein paar Werte größer und ein paar Werte kleiner Null
Wähle hier $$- 3, - 2, - 1, 0, 1, 2, 3$$ als x-Werte. - Schritt: Setze jeden einzelnen x-Wert in die Funktionsgleichung ein und berechne den entsprechenden y-Wert.
$$y=f( $$ $$-3$$ $$ )$$ $$=2*($$$$-3$$$$)=-6$$
$$y=f($$$$-2$$$$)=2*($$$$-2$$$$)=-4$$
$$y=f($$$$-1$$$$)=2*($$$$-1$$$$)=-2$$
$$y=f($$$$0$$$$)=2* $$$$0$$$$=0$$
$$y=f($$$$1$$$$)=2*$$$$1$$$$=2$$
$$y=f($$$$2$$$$)=2*$$$$2$$$$=4$$
$$y=f($$$$3$$$$)=2*$$$$3$$$$=6$$x y - 3 - 6 - 2 - 4 - 1 - 2 0 0 1 2 2 4 3 6
| x | y |
|---|---|
| - 3 | |
| - 2 | |
| - 1 | |
| 0 | |
| 1 | |
| 2 | |
| 3 |
Graph aus einer Wertetabelle zeichnen
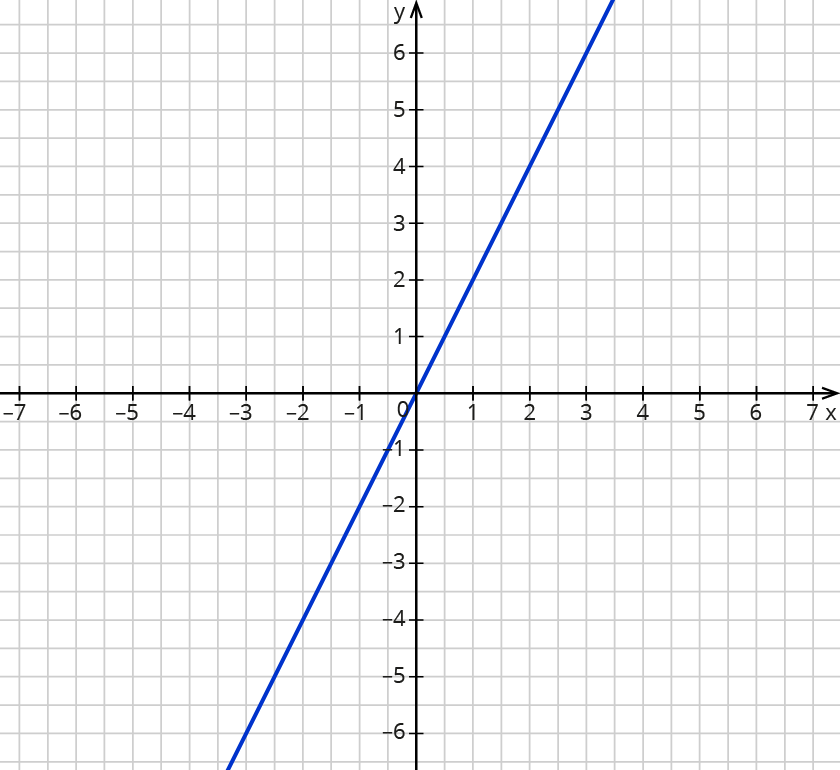
Trage die Punkte aus der Wertetabelle in ein Koordinatensystem ein und zeichne den Graphen der Funktion.
| x | y |
|---|---|
| - 3 | - 6 |
| - 2 | - 4 |
| - 1 | - 2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
Gehe so vor:
- Schritt: Zeichne ein Koordinatensystem und wähle eine günstige Achseneinteilung. Alle Punkte aus der Wertetabelle müssen eingetragen werden können.
Wähle 2 Kästchen als eine Einheit. - Schritt: Trage die Punkte aus der Wertetabelle in das Koordinatensystem ein.
- Schritt: Zeichne durch die Punkte eine Gerade.
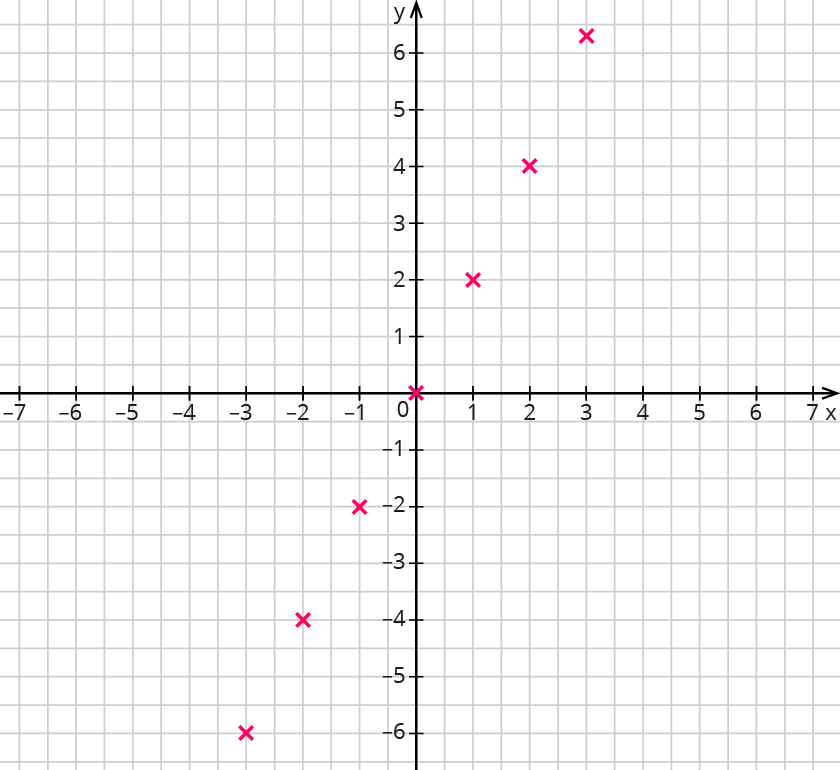
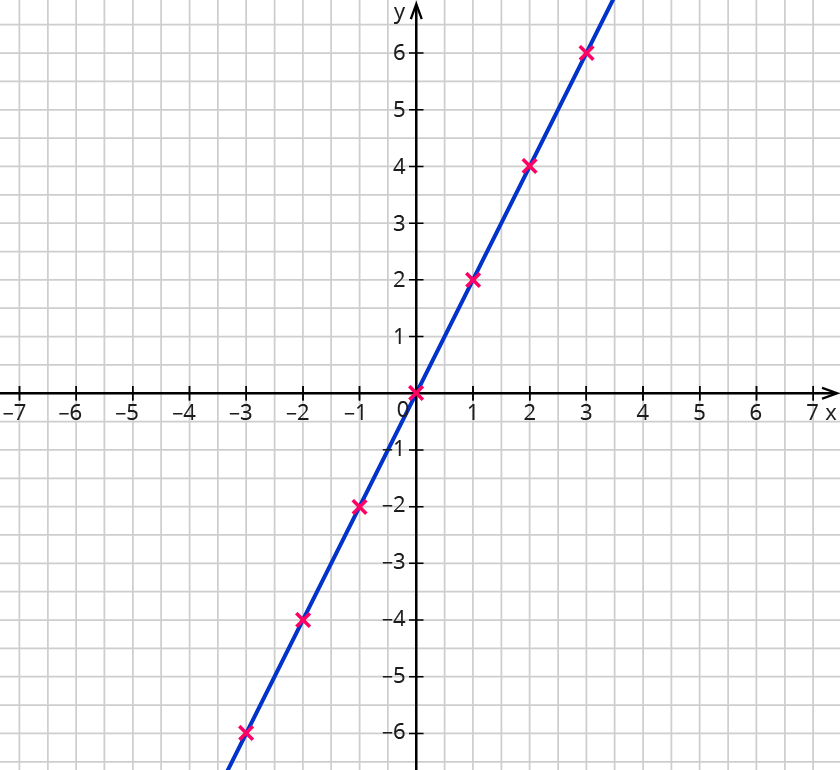
Eine Gerade ist schon durch 2 Punkte festgelegt. Wenn du nur den Graphen der proportionalen Funktion einzeichnen sollst, reichen 2 Punkte aus der Wertetabelle.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Funktionsgleichung aus Sachzusammenhang erstellen
Anna möchte im Supermarkt Süßigkeiten kaufen. Für 2 Tüten Süßigkeiten muss Anna 4 € bezahlen.
Gib die Funktionsgleichung für die proportionale Funktion Anzahl an Tüten $$rarr$$ Preis (in €) an.
Gehe so vor:
1. Schritt: Überlege, worum es in der Aufgabe geht.
Es geht um Tüten mit Süßigkeiten und deren Preis.
2. Schritt: Entnehme der Aufgabe ein gegebenes Wertepaar.
2 Tüten kosten 4 €.
3. Schritt: Berechne m. Bilde dazu den Quotienten $$y/x = m$$.
$$m= 4/2=2$$
4. Schritt: Setze m in die allgemeine Funktionsgleichung $$f(x)=mx$$ ein.
$$f(x)=2x$$
Die Zuordnungsvorschrift ordnet jedem x genau ein y zu: x $$rarr$$ y.
Den Quotienten nennt man auch Proportionalitätsfaktor.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen