Schnittpunkte zweier linearer Funktionen bestimmen
Schnittpunkte linearer Funktionen
Wenn 2 Graphen von linearen Funktionen sich schneiden, haben sie einen gemeinsamen Punkt.
Das ist der Schnittpunkt der beiden linearen Funktionen.
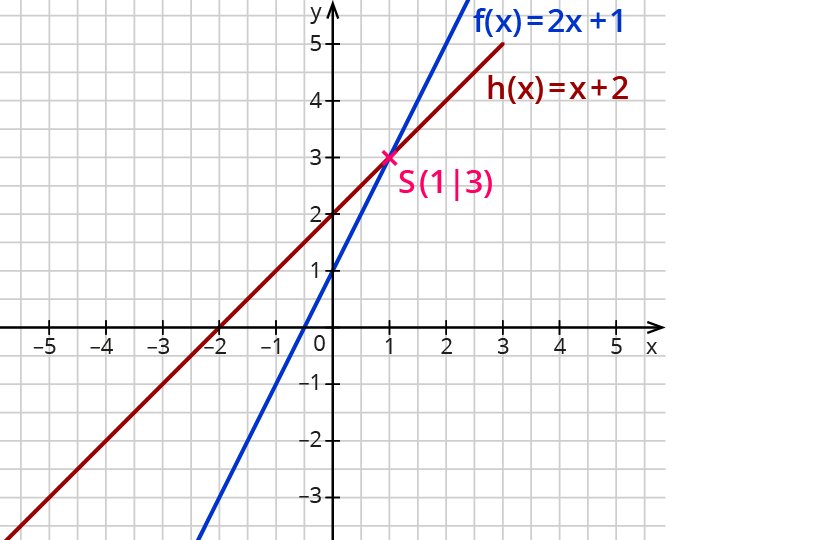
Hier die Funktionsgleichungen und der Schnittpunkt:
- $$f(x)= 2x+1 $$
- $$h(x)= x+2$$
- Schnittpunkt $$S(1|3)$$
Als gemeinsamer Punkt erfüllt der Schnittpunkt beide Funktionsgleichungen:
$$f(1)=2*1+1=3 $$
$$h(1)=1+2=3$$
Also ist der Punkt $$S (1|3)$$ der Schnittpunkt von $$f(x)$$ und $$h(x)$$.
Zwei lineare Funktionen schneiden sich maximal in einem Punkt.
Schnittpunkte bestimmen
Du kannst den Schnittpunkt von linearen Funktionen auf zwei Arten bestimmen:
- rechnerisch
- grafisch
Das grafische Bestimmen des Schnittpunktes kann ungenau sein, da du den Schnittpunkt manchmal nicht exakt ablesen kannst.
Durch eine Rechnung erhältst du immer den genauen Schnittpunkt.
Schnittpunkte grafisch bestimmen
Bestimme den Schnittpunkt von $$f(x)=4x$$ und $$h(x)=2x+2$$.
Gehe zum grafischen Bestimmen des Schnittpunktes so vor:
1. Schritt: Zeichne die Funktionen in ein Koordinatensystem ein.
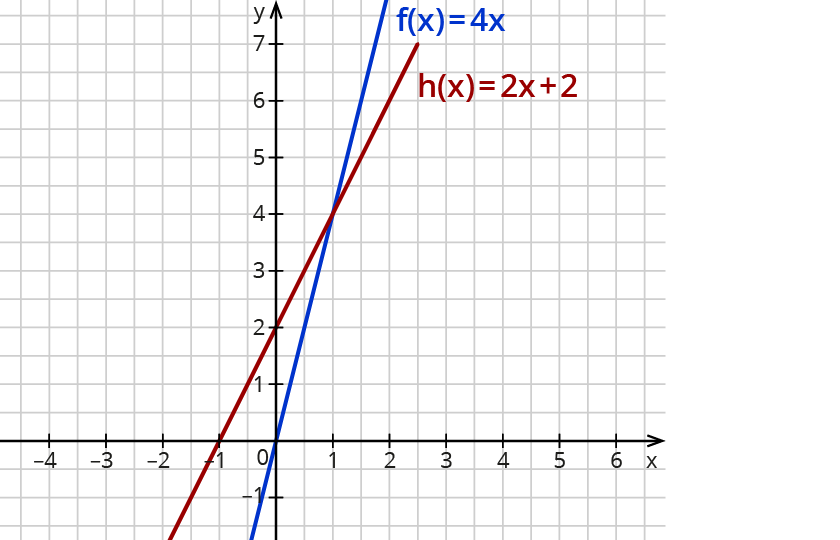
2. Schritt: Markiere den Schnittpunkt durch ein Kreuz und lies dessen Koordinaten ab.
Beschrifte den Schnittpunkt.
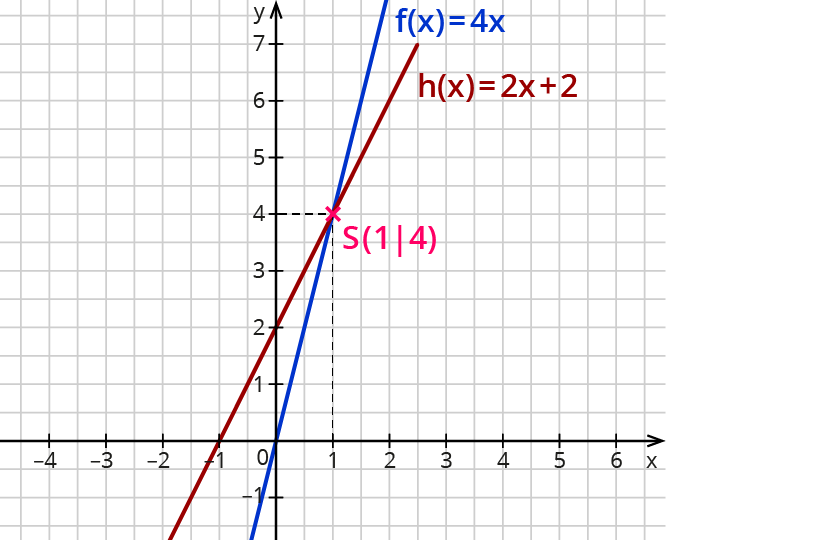
Die Koordinaten des Schnittpunktes lauten $$(1|4)$$.
$$S(x|y)$$;
erst $$x$$, dann $$y$$.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Schnittpunkte rechnerisch bestimmen
Bestimme den Schnittpunkt von $$f(x)=1/3 x +1$$ und $$h(x)=2x + 1/2$$.
Gehe folgendermaßen vor:
1. Schritt: Setze beide Funktionsgleichungen gleich.
$$f(x)=h(x)$$
$$1/3 x +1 = 2x + 1/2$$
2. Schritt: Löse die Gleichung nach $$x$$ auf.
$$1/3 x +1 = 2x + 1/2 | -1/2$$
$$1/3 x + 1/2 = 2x | -1/3 x$$
$$1/2 = 5/3 x | : 5/3$$
$$3/10 = x$$
$$x= 3/10 $$
Man teilt durch einen Bruch, indem man mit dem Kehrwert multipliziert.
Schnittpunkt rechnerisch bestimmen
3. Schritt: Bestimme $$y$$. Setze dazu $$x$$ in eine der beiden Funktionsgleichungen ein.
$$x= 3/10$$ einsetzen in $$h(x)$$
$$y = h(3/10 ) = 2*3/10 + 1/2$$
$$y= 11/10 $$
4. Schritt: Probe.
$$h(3/10 ) = 2*3/10 + 1/2 = 11/10$$
$$f(3/10)=1/3 *3/10 +1= 3/30 +1 = 1/10 + 10/10 = 11/10 $$
5. Schritt: Gib den Schnittpunkt an.
$$f(x)$$ und $$h(x) $$ schneiden sich im Punkt $$S (3/10| 11/10 )$$.
Tipp: Wähle die Funktionsgleichung geschickt aus. Oft ist das Berechnen von $$y$$ mit einer Funktionsgleichung einfacher.
$$S(x|y)$$;
erst $$x$$, dann $$y$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen