Lineare Funktionen in der Praxis

Alles viel zu theoretisch mit den Funktionen? Hier siehst du 3 Anwendungen:

Produktkosten

Eine Maschinenfabrik produziert die Ketten für Kettensägen.
Das Einrichten der einzelnen notwendigen Maschinen kostet 4500 €, die Herstellung jeder Kette 9 €.

Du erkennst, dass die Kosten der Ketten abhängig von der Anzahl der Ketten sind.

Diese Kosten sind variabel: Je mehr Ketten, desto höher die Kosten.

Der Einrichtungspreis der Maschinen ist fix. Er ändert sich nicht.

So heißt die Funktion $$k(x) = 9x + 4500$$

• $$x$$ Anzahl der Ketten
  
• $$k$$ Kosten

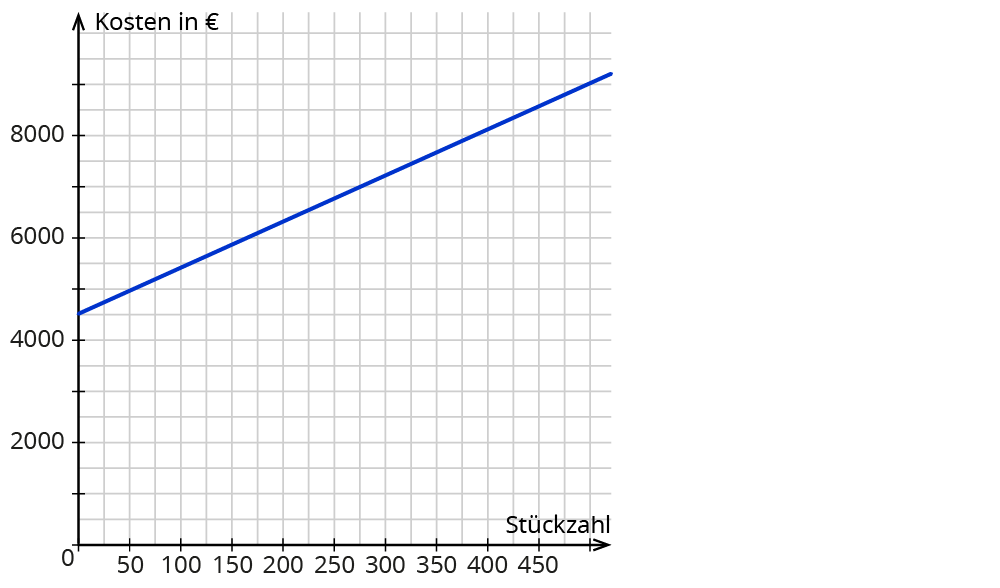
Das ist die Kostenfunktion zur Herstellung der Ketten.

Umsatz und Kosten

Für den Fabrikchef ist aber vor allem der Gewinn interessant.

Dazu berechnet er erstmal den Umsatz. Das ist das Geld, das er durch den Verkauf der Ketten einnimmt.

Nach zahlreichen Recherchen setzt der Chef den Verkaufspreis von 20 € pro Kette an.

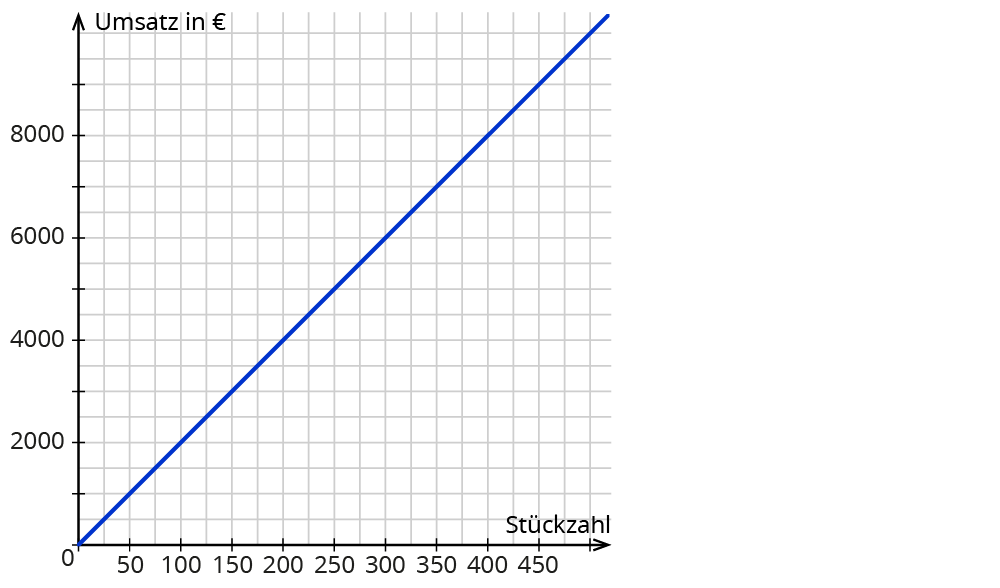
Hieraus ergibt sich die Funktion $$u(x) = 20x$$.

• $$x$$ Anzahl der Ketten
  
• $$u$$ Umsatz

Gewinn

Frage: Wie viele Ketten müssen hergestellt werden, damit die Firma einen Gewinn erzielt?

Zeichne beide Graphen in ein Koordinatensystem:

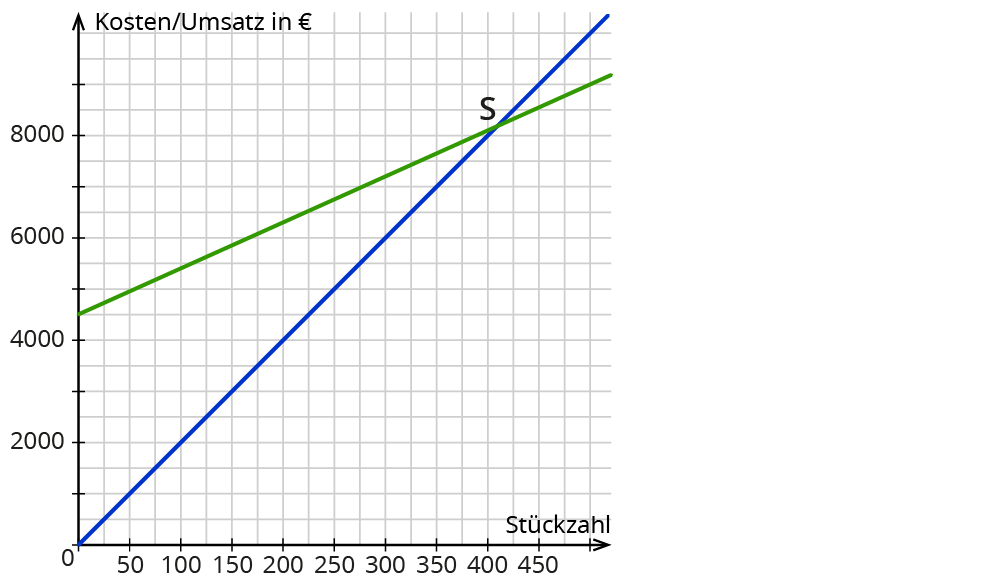
Du erkennst, liegt der Umsatz bei ungefähr 400 Stück über den Kosten.

Das heißt: Ab dieser Stückzahl erzielt das Unternehmen einen Gewinn.

Genau kannst du diese Grenze rechnerisch ermitteln:

$$9x + 4500 = 20x$$   $$| -9x$$
$$4500 = 11x$$   $$| :11$$
$$x = 409,1$$

Der errechnete Wert bedeutet, dass ab 410 verkauften Ketten der Umsatz größer ist als die Kosten: die Firma macht einen Gewinn.

Gewinnfunktion

Für den Gewinn ist auch eine Funktionsgleichung praktisch: Ziehe vom Umsatz die Kosten ab.

$$g(x) = u(x) – k(x)$$

$$g(x) = 20x – ( 9x + 4500 )$$

$$g(x) = 11x – 4500$$

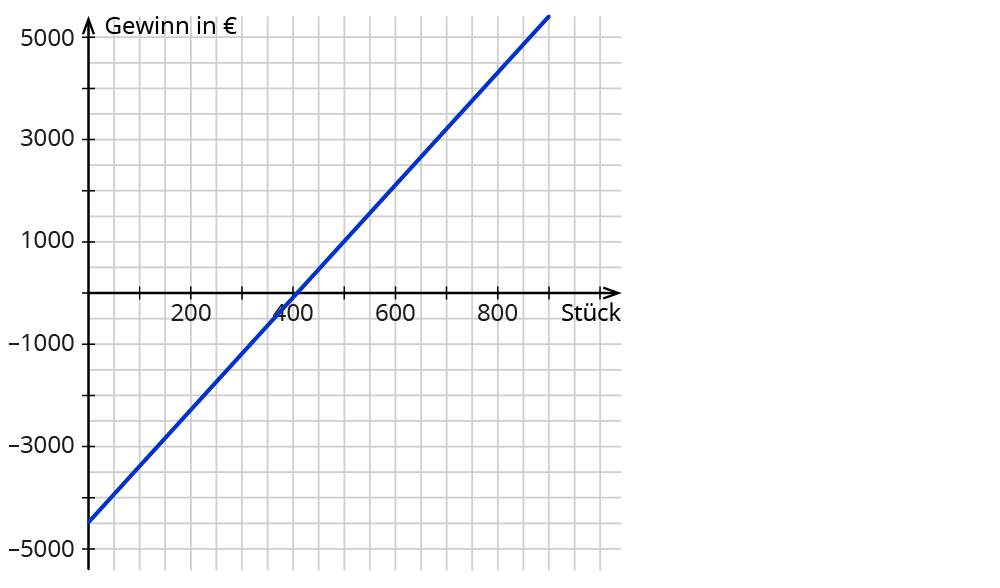
Du siehst, dass die Gerade bei etwas über 400 Stück die $$x$$-Achse schneidet.
Bei einer geringeren Stückzahl ist der Gewinn negativ (Verlust), danach positiv (Gewinn).

Die Vermutung liegt nahe, dass der Schnittpunkt bei $$x = 409,1$$ liegt.
Das ist der Schnittpunkt von $$u(x)$$ und $$k(x)$$ )

$$11x – 4500 = 0$$   $$ | +4500$$

$$11x = 4500$$   $$| :11$$

$$x = 409,1$$

Zweites Angebot

Bevor es zu einer endgültigen Entscheidung kommt, liegt noch ein zweites Kostenangebot vor. Der Einrichtungspreis für die Maschinen erhöht sich um 2500 € auf 7000 €, der Herstellungspreis für die einzelne Kette reduziert sich hingegen um 4 € pro Stück.

Somit ergibt sich die Kostenfunktion $$k_n(x) = 5x + 7000$$.

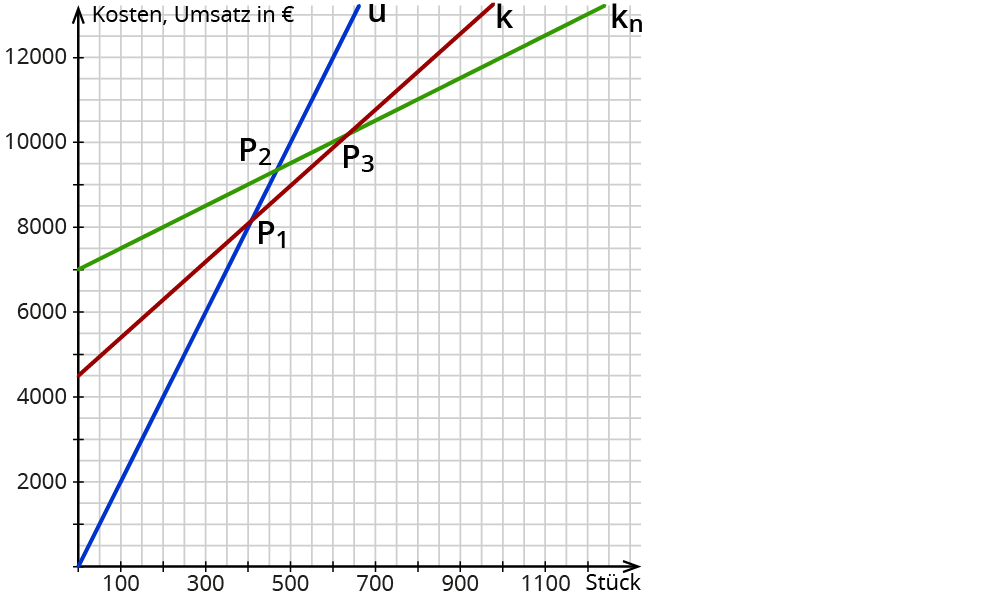
Interessant sind nun die drei Schnittpunkte

• $$P_1$$ ($$u$$ und $$k$$),
• $$P_2$$ ($$u$$ und $$k_n$$) und
• $$P_3$$ ($$k$$ und $$k_n$$).

Den ersten hast du bereits ermittelt ($$x = 409,1$$).
Er besagt, dass bei bestehenden Kosten ab 410 verkauften Ketten ein Gewinn erzielt wird.

Setzt du $$u = k_n$$, so erhältst du $$P_2$$.

$$20x = 5x + 7000$$   $$| -5x$$

$$15x = 7000$$   $$| :15$$

$$x = 466,67$$

Das bedeutet, dass ab einer Stückzahl von 467 ebenfalls ein Gewinn bei den neuen Produktionskosten erzielt wird.

Entscheidungen…

Für den Chef jedoch ist interessant, welche Produktionskosten einen höheren Gewinn einbringen.
Für diese Berechnung setzt du $$k = k_n$$.   $$(P_3)$$

$$9x + 4500 = 5x + 7000$$   $$| -4500$$

$$9x = 5x + 2500$$   $$| -5x$$

$$4x = 2500$$   $$| :4$$

$$x = 625$$

Das bedeutet, dass bei einer Stückzahl von über 625 die neuen Produktionskosten niedriger sind und somit einen höheren Gewinn gewährleisten.

Gewinnfunktionen

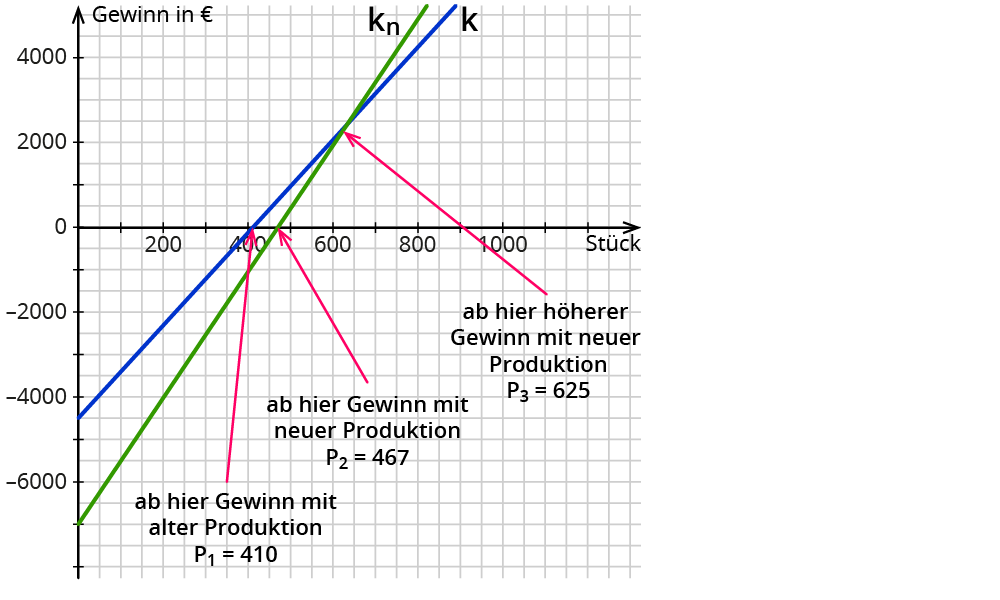
Diese Erkenntnis kannst du in den Gewinnfunktionen $$g$$ und $$g_n$$ verdeutlichen:

$$g(x) = 11x – 4500$$         (alt)

$$g_n = u - k_n$$
$$g_n(x) = 20x – ( 5x + 7000 )$$
$$g_n(x) = 15x – 7000$$       (neu)