Funktionsgleichung aus Graph ablesen

Eine lineare Funktion hat die Funktionsgleichung $$f(x)=m*x+b$$.

Bestimme die Funktionsgleichung von $$f$$ , indem du 2 Werte aus dem Graphen abliest:

• Steigung $$m$$
• $$y$$-Achsenabschnitt $$b$$

Schrittfolge zum Ablesen

Bestimme die Funktionsgleichung des Graphen:

1. Schritt: Lies den Schnittpunkt $$S(0|b)$$ mit der $$y$$-Achse ab.

$$S(0|-2)$$. Damit ist $$b=-2$$.

2. Schritt: Gehe von diesem Punkt aus nach rechts und dann nach oben oder unten, bis du beim Graphen ankommst.
Gehe 1 nach rechts und 4 nach oben. Damit ist $$m=4/1 = 4$$.

3. Schritt: Setze $$m$$ und $$b$$ in die allgemeine Funktionsgleichung $$f(x)=mx+b$$ ein.

$$b=-2$$ und $$m= 4$$ einsetzen: $$ f(x)= 4x-2$$ .

Übersicht: Steigung ablesen

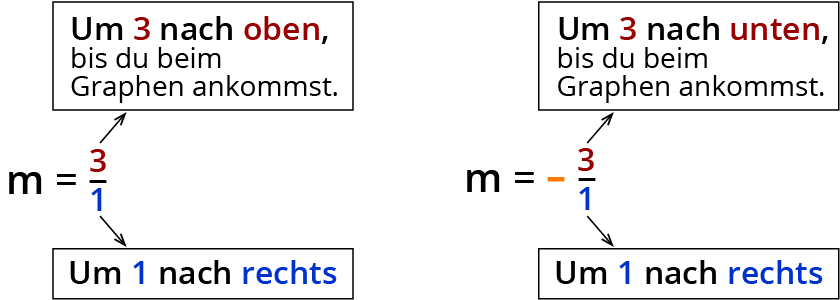
Beispiele:

1) nach rechts und nach oben gehen

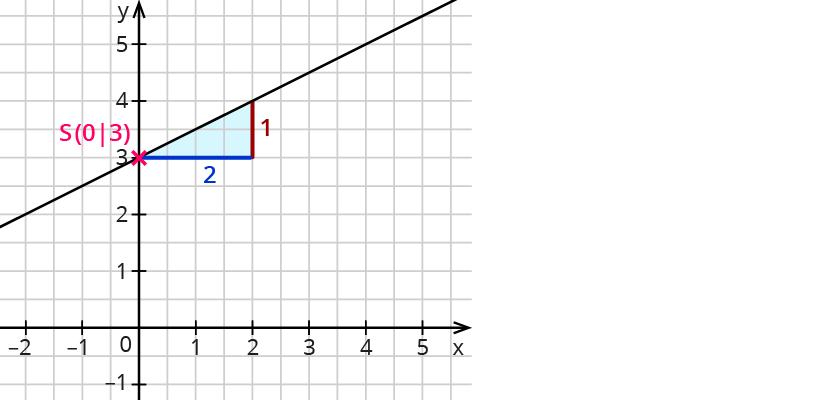
1. Schritt: Lies den Schnittpunkt des Graphen mit der $$y$$-Achse ab: $$S(0|3)$$. Damit ist $$b=3$$.

2. Schritt: Gehe von diesem Punkt aus um 2 nach rechts und um 1 nach oben. Damit ist $$m=1/2=0,5$$.

3. Schritt: Setze $$b=3$$ und $$m=0,5$$ in die allgemeine Funktionsgleichung ein: $$f(x)=0,5x+3$$.

Beispiele

2) nach rechts und nach unten gehen

Bestimme die Funktionsgleichung des Graphen.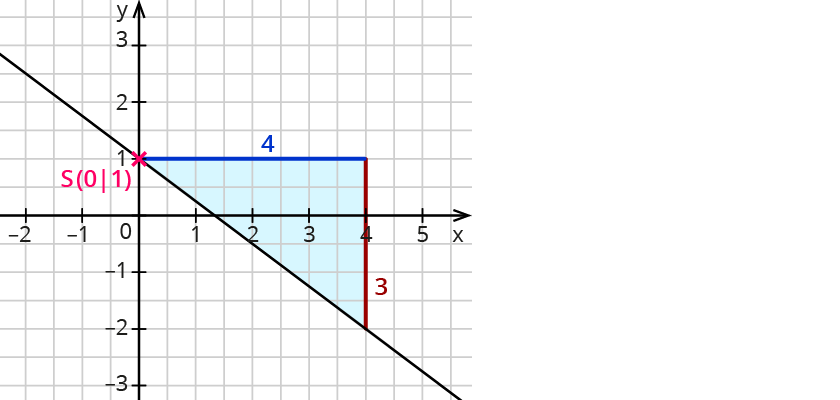

1. Schritt: Lies den Schnittpunkt des Graphen mit der $$y$$-Achse ab: $$S(0|1)$$. Damit ist $$b=1$$.

2. Schritt: Gehe von diesem Punkt aus um 4 nach rechts und um 3 nach unten. Damit ist $$m = - 3/4$$.

3. Schritt: Setze $$b=1$$ und $$m= - 3/4$$ in die allgemeine Funktionsgleichung ein:
$$f(x)= - 3/4x+1$$.

Eigene Funktionsgleichungen

Probier es jetzt einmal selbst aus! Verschiebe beide Punkte und beobachte die Veränderung von b und m.

Seid ihr zu zweit? Blende die Funktionsgleichung mit dem Häkchen aus und verändere die Gerade. Dein Partner/deine Partnerin soll nun die zugehörige Gleichung aufschreiben. Dann tauscht ihr.