Baumdiagramm - einstufiges Zufallsexperiment

Bei vielen Zufallsexperimenten kannst du dir mit diesen Bildern einen Überblick über die Ergebnisse machen. Das sind die Baumdiagramme.

Beispiel: Reißzweckenwurf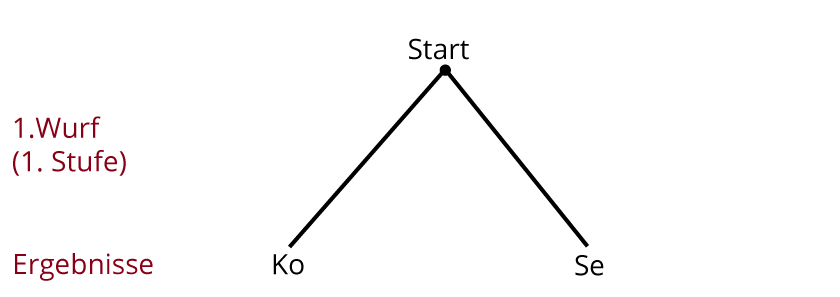

• Ko = Kopf
• Se = Seite

Die Reißzwecke wurde nur einmal geworfen. Das ist dann ein einstufiges Zufallsexperiment mit $$Omega$$ = {Ko, Se}.
Dieser Baum besteht aus nur einer Stufe, deren Zweige hier Pfade der Länge 1 bilden.

Ergebnis eines Zufallsexperiments

Jeder Ausgang eines Zufallsexperiments heißt Ergebnis. Die Menge aller Ergebnisse bildet die Ergebnismenge $$Omega$$.
Beispiel: Münzwurf: $$Omega$$ = {Wappen, Zahl}
Die Anzahl der Ergebnisse ist |$$Omega$$| = 2.

Baumdiagramm - mehrstufiges Zufallsexperiment

Zufallsexperimente wie das Werfen einer Reißzwecke kannst du mehrmals durchführen. Dann heißt das Zufallsexperiment mehrstufig.

Wenn du 2mal die Reißzwecke wirfst, sieht das Baumdiagramm so aus:

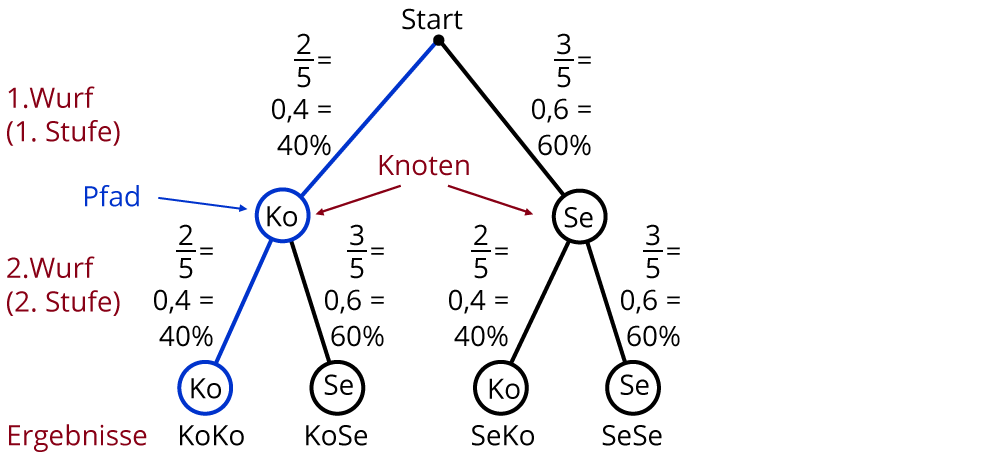
Es ist ein zweistufiges Experiment. Der Baum besteht aus zwei Stufen. Die Zweige sind Pfade der Länge 2. An den Pfaden stehen die Wahrscheinlichkeiten als Brüche, Dezimalzahlen oder Prozentzahlen.

Am Ende der Pfade stehen die Ergebnisse des mehrstufigen Zufallsexperiments.

Die Ergebnismenge lautet $$Omega$$ = {KoKo; KoSe; SeKo; SeSe} mit |$$Omega$$| = 4 als Anzahl der Ergebnisse.

Ereignis und Gegenereignis

Baumdiagramme können sehr groß werden. Du siehst hier ein zweistufiges Baumdiagramm.
Das Zufallsexperiment ist: Du würfelst zweimal hintereinander mit einem Würfel. Du willst wissen, wie groß die Chance für einen 6er-Pasch ist: E = {Pasch 6}, also das Auftreten von 2-mal 6.

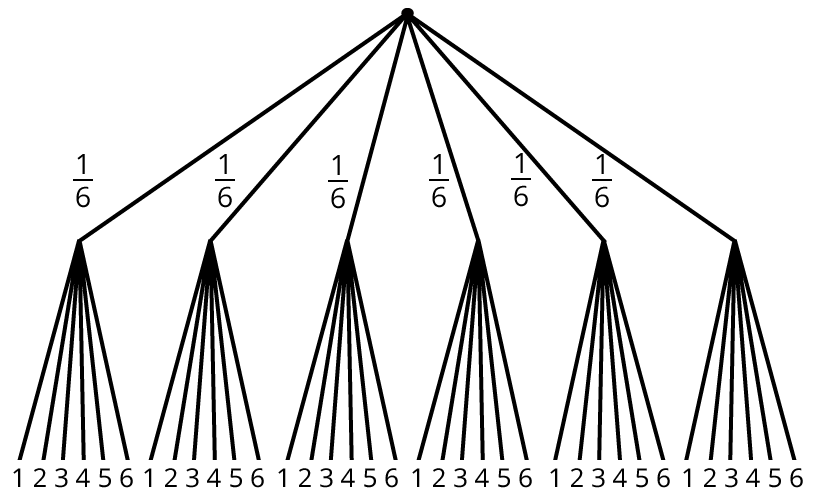
Wenn du ein Zufallsexperiment mit Ereignis und Gegenereignis beschreiben kannst, wird das Baumdiagramm viel übersichtlicher. Das Bild unten zeigt dir diese Möglichkeit für die Chance E = {Pasch 6} und $$bar E$$ = {kein Pasch 6}.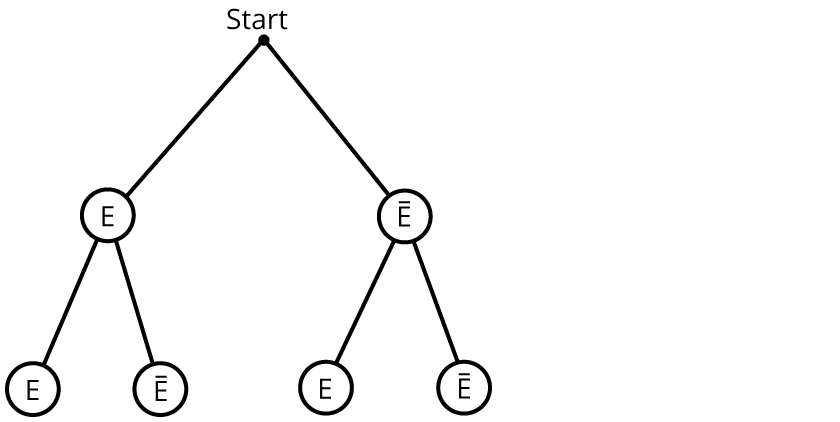

Ereignis und Gegenereignis

Es gibt Zufallsexperimente, bei denen nur interessiert, ob ein Ereignis $$E$$ eintritt oder nicht. Wenn $$E$$ nicht eintritt, so tritt das Gegenereignis $$bar E$$ ein. Beispiele:
Losverkauf: $$E$$ = {Treffer}, $$bar E$$ = {Niete} Würfelwurf: $$E$$ = {6}, $$bar E$$ = {1, 2, 3, 4, 5}
Regel: Es gilt $$p(E) + p(bar E) = 1$$

Dreistufige Baumdiagramme

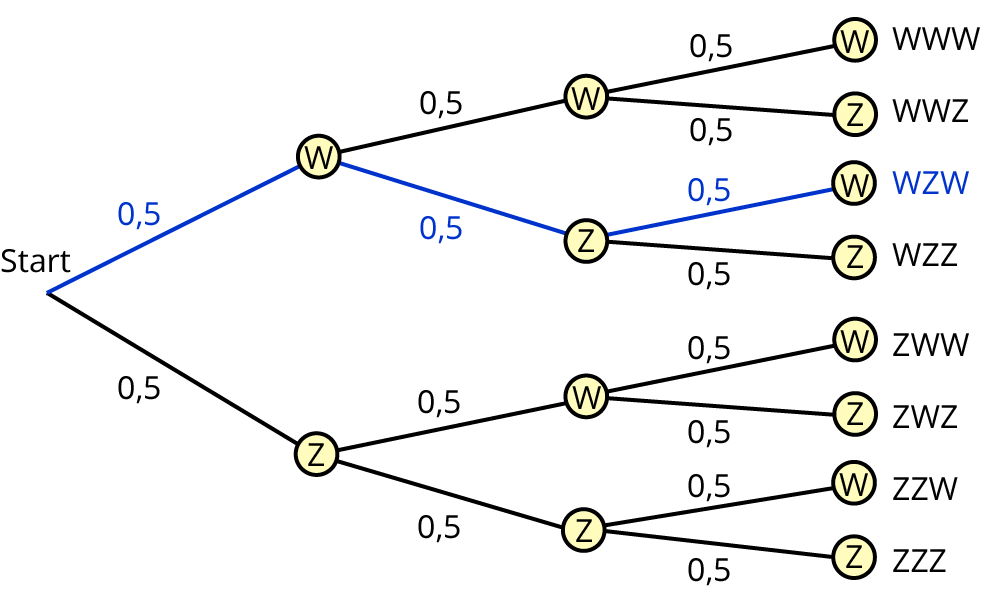
Du siehst hier ein Baudiagramm für einen dreifachen Münzwurf. Der Baum besteht aus drei Stufen. Zu jedem möglichen Ergebnis gehört ein Pfad, der am Start beginnt und über die zugehörigen Knoten bis zur letzten Stufe verläuft. Der blaue Pfad ist das Ergebnis WZW.

Hier gilt: $$Omega$$ = {WWW, WWZ, WZW, WZZ, ZWW, ZWZ, ZZW, ZZZ} mit |$$Omega$$| =8.

Baumdiagramme, Pfade und Wahrscheinlichkeiten

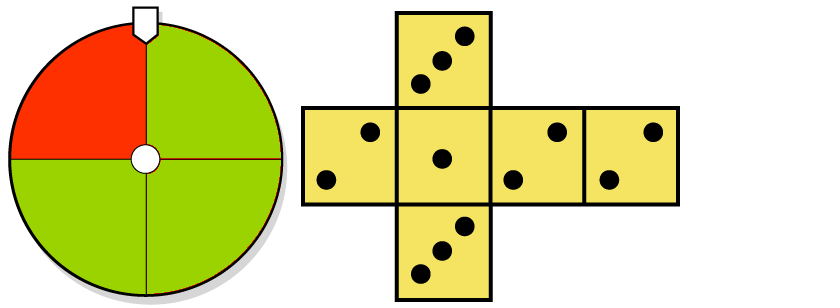
Das Zufallsexperiment setzt sich zusammen:

1. Glücksrad drehen
   Beim Glücksrad sind die Flächen rot und grün eingefärbt
2. Würfeln
   Würfel mit dem abgebildeten Netz trägt die Nummern 1, 2 und 3.

Es kommt hier nicht auf die Reihenfolge der einzelnen Ergebnisse an.

Die Baumdiagramme zeigen dir die möglichen Ergebnisse.
Bei diesem Zufallsexperiment ist egal, ob du erst das Glücksrad drehst oder erst würfelst. Die Wahrscheinlichkeiten für die Ergebnisse bleiben gleich.

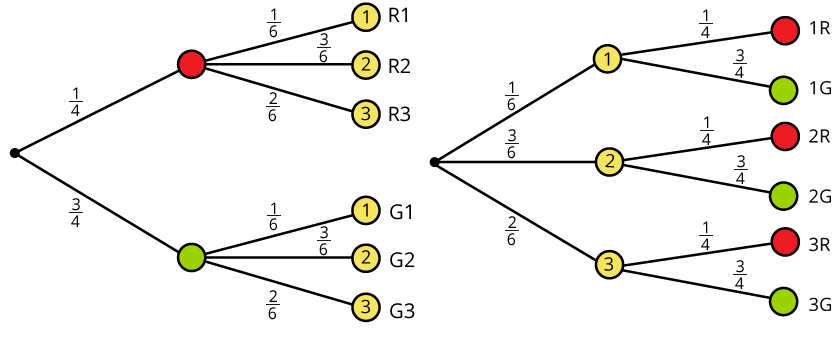
Wahrscheinlichkeiten

Linkes Baumdiagramm: Wahrscheinlichkeit für R 2 beträgt
3/6 von 1/4, also (3/6) $$*$$ (1/4) = 3/24 = 1/8

Rechtes Baumdiagramm: Wahrscheinlichkeit für 2 R beträgt
1/4 von 3/6, also (1/4) $$*$$ (3/6) = 3/24 = 1/8

Damit gilt: p(R 2) = p(2 R) = 1/8.

Baumdiagramm und Multiplikationsregel

Ein Kasten enthält 8 rote (R) Kugeln und eine grüne (G) Kugel. Firas zieht eine Kugel, notiert die Farbe und legt sie wieder zurück.

Das ist das Baumdiagramm für das dreistufige Zufallsexperiment.

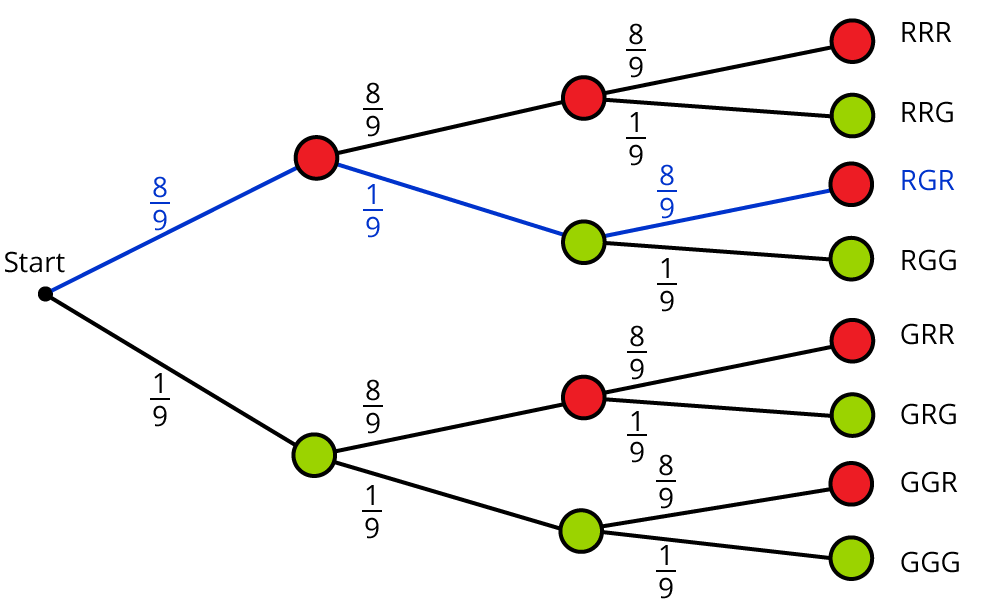
Das ErgebnisRGR wird, wie beim zweistufigen Zufallsexperiment der letzten Seite, aus dem Produkt der Wahrscheinlichkeiten längs des blauen Pfades berechnet: p(RGR) $$= \frac{8}{9} * \frac{1}{9} * \frac{8}{9} = \frac{64}{729}$$.

Diese Regel gilt für alle mehrstufigen Zufallsexperimente.