Genau - mindestens - höchstens

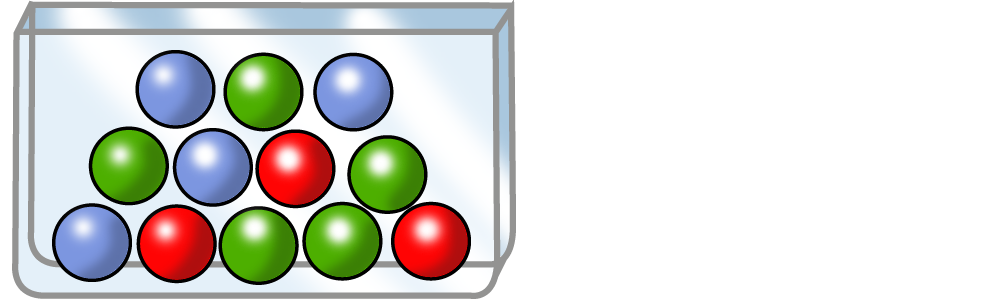
In einer Urne liegen vier blaue (B), fünf grüne (G) und drei rote (R) Kugeln.
Es sollen zwei Kugeln entnommen werden.
Dabei werden die nachfolgend angegebenen Ereignisse erläutert.
Um die Begriffe zu erklären, werden jeweils die Ergebnisse betrachtet, bei denen die dazugehörenden Ereignisse eintreten.

Genau

E: „genau eine Kugel ist rot“
E = {BR, GR} - es ist genau nur eine rote Kugel unter den zwei möglichen vorhanden.

Mindestens

F: „mindestens eine Kugel ist blau“
F = {BB, BR, BG} - unter den zwei Kugeln muss sich eine blaue Kugel befinden, es können aber auch zwei blaue Kugeln sein.

Höchstens

G: „höchstens eine Kugel ist grün“
G = {BG, RG, BB, RR, RB} - unter den zwei Kugeln darf sich nur eine grüne Kugel befinden, es können aber auch keine grünen Kugeln auftreten.

Baumdiagramm - Ergebnisse und Ereignis

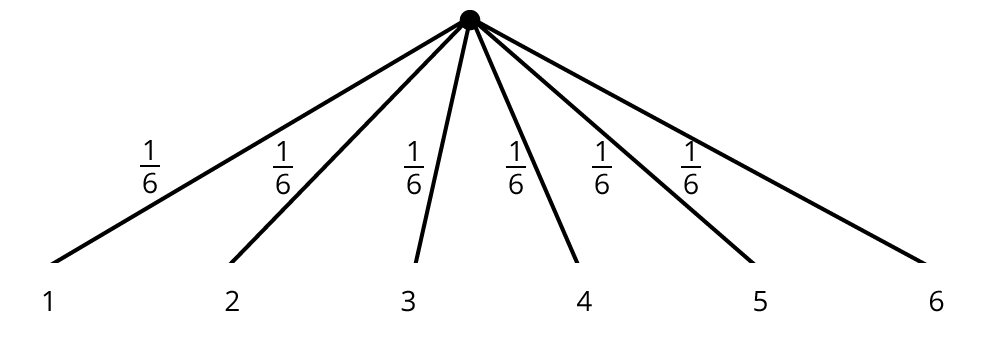
Ergebnis

Du siehst hier ein Baumdiagramm für einen Würfelwurf. Es gibt 6 mögliche Ergebnisse: Die Augenzahlen 1 bis 6. Damit liegt die Ergebnismenge $$Omega$$ fest: $$Omega = {1, 2, 3, 4, 5, 6}$$.

Ereignis

Interessiert nur das Werfen einer ungeraden Zahl, so lässt sich das Ereignis E: „ungerade Zahl“ durch die Ergebnismenge E = {1, 3, 5} darstellen.

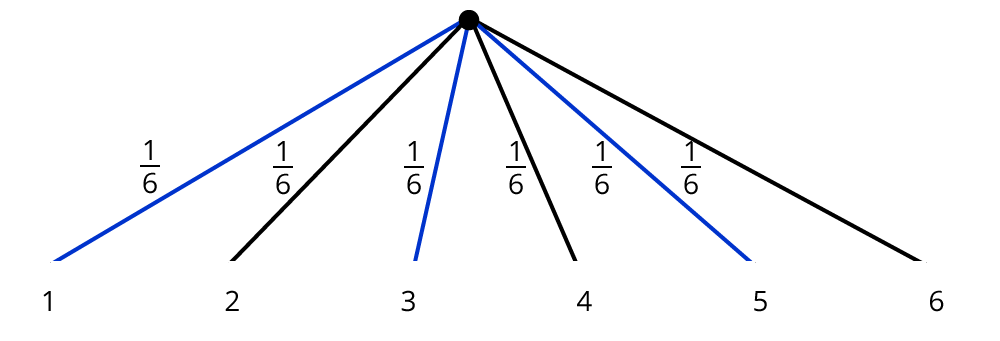
Das Ereignis E ist eine Teilmenge von $$Omega$$.

Baumdiagramm und Summenregel

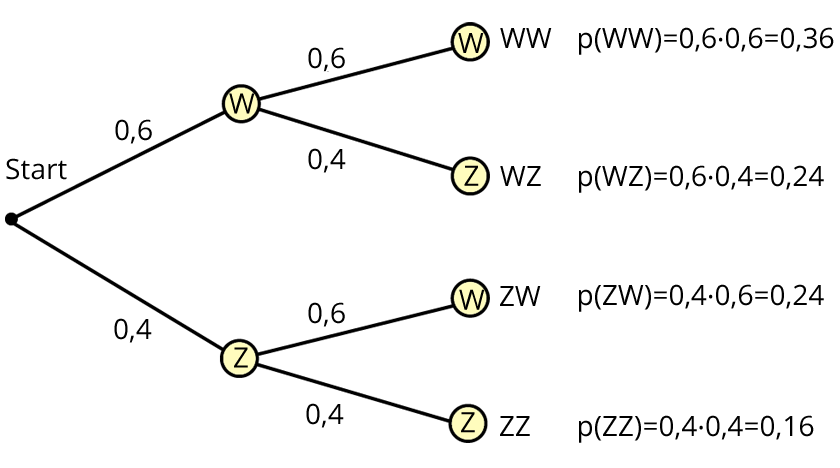
Beispiel: Eine gezinkte Münze wird zweimal geworfen.
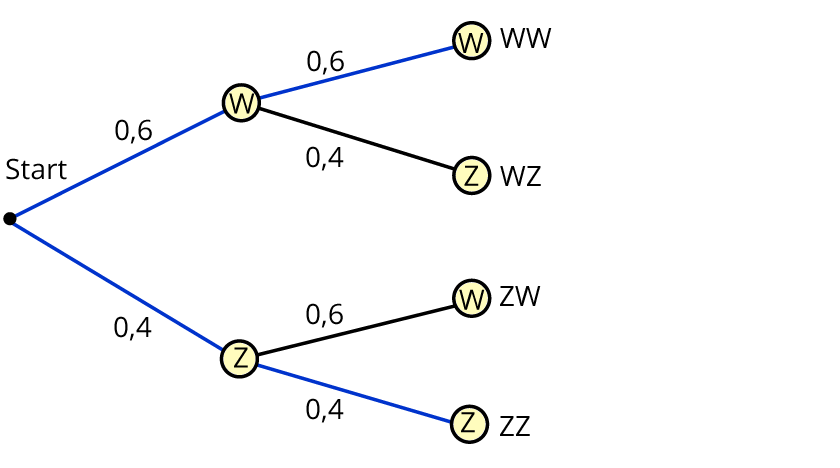
Du siehst im zweistufigen Baumdiagramm die Ergebnismenge
$$Omega = {$$WW, WZ, ZW, ZZ$$}$$.

Wahrscheinlichkeit für Wappen: p(W) = 0,6
Wahrscheinlichkeit für Zahl: p(Z) = 0,4

Zu jedem Ergebnis gibt es einen Pfad. Die Pfadwahrscheinlichkeiten ergeben sich aus der Produktregel.
Beispiel: p(WW) = 0,6 $$*$$ 0,6 = 0,36

Das Ereignis E: „gleiche Seite oben“ besteht aus den beiden Ergebnissen
WW und ZZ: E = {WW, ZZ}.

Wahrscheinlichkeit für Ereignis E:
p(E) = p(WW) + p(ZZ) = 0,36 + 0,16 = 0,52

Produktregel

Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt
der Wahrscheinlichkeiten längs eines Pfades.
Beispiel: p(WW) = 0,6 $$*$$ 0,6 = 0,36

Summenregel - Ereignis und Gegenereignis

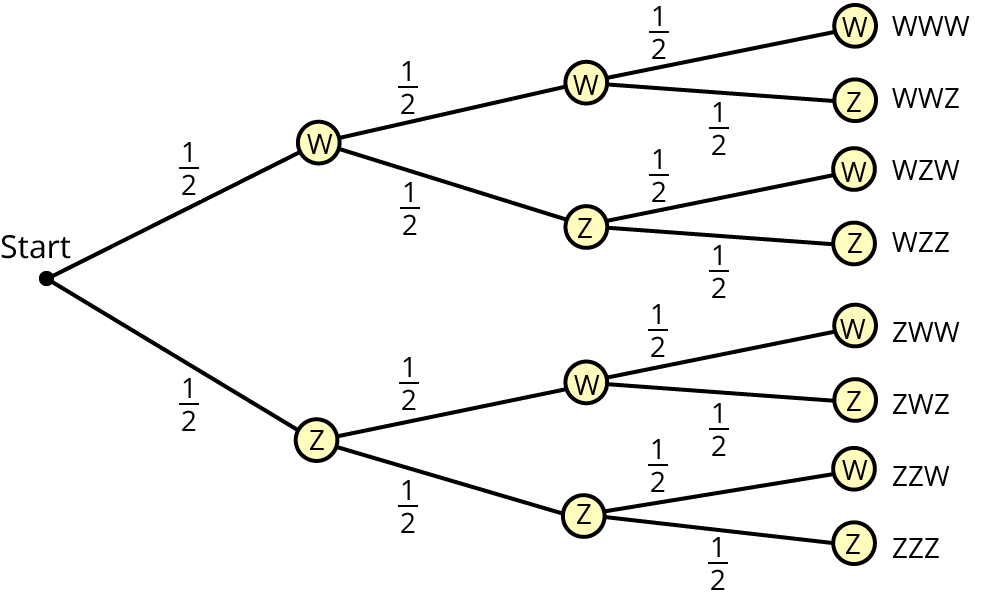
Du siehst das Baumdiagramm für einen dreifachen Würfelwurf mit einer normalen Münze.
$$Omega = {$$WWW, WWZ, WZW, WZZ, ZWW, ZWZ, ZZW, ZZZ$$}$$.

Berechne die Wahrscheinlichkeit für
E: „mindestens einmal fällt Wappen (W)“.

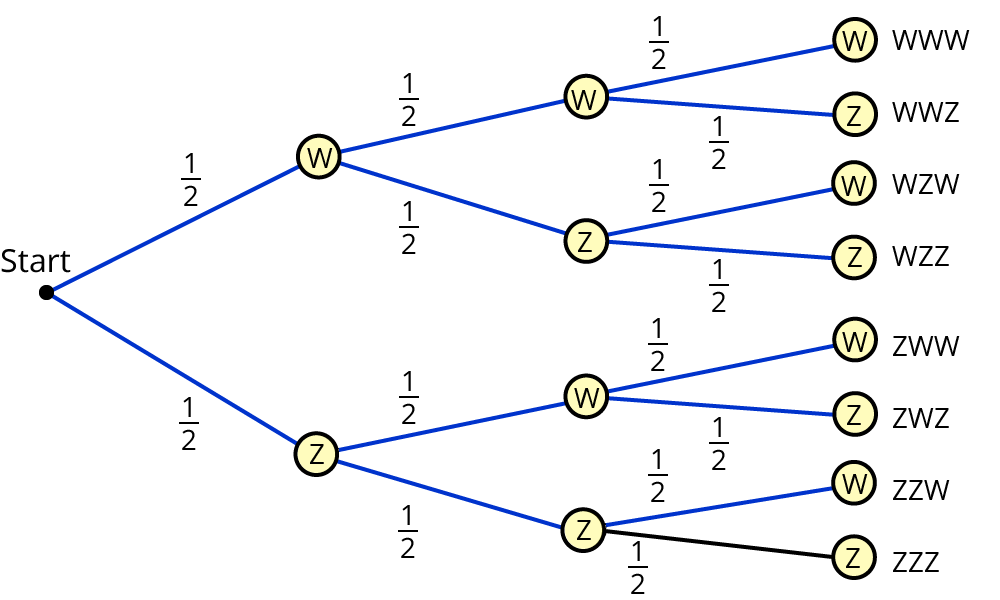
Damit wäre $$E = {$$WWW, WWZ, WZW, WZZ, ZWW, ZWZ, ZZW$$}$$.

Lösung mit der Summenregel:
p(E)=p(WWW)+p(WWZ)+p(WZW)+p(WZZ)+p(ZWW)+p(ZWZ)+p(ZZW)

$$= 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8$$

$$= 7/8$$
Beachte: p(WWW) = $$1/2 * 1/2 * 1/2$$= $$1/8$$

Lösung mit dem Gegenereignis:
$$p(E) = 1 - p( bar E )= 1 -1/8 = 7/8$$
Manchmal ist es schneller, die Wahrscheinlichkeit mit dem Gegenereignis auszurechnen.
$$bar E$$: „kein Wappen“