Erwartungswerte berechnen
Glücksrad

Tom und Ida spielen mit dem Glücksrad. Es hat gerade Taschengeld gegeben. Tom schlägt Ida ein Spiel vor:
„Wenn du das Rad drehst und es kommt GRÜN (G), gibst du mir 50 Cent, kommt ROT (R), gebe ich dir 20 Cent.“
Was meinst du, sollte sich Ida auf dieses Spiel einlassen?
Du siehst die Wahrscheinlichkeit für die Farben im Glücksrad. Wenn Tom und Ida etwa 100mal drehen, wird Tom 40mal 50 Cent, also 2000 Cent oder 20 € von Ida erwarten. Ida hingegen wird von Tom 60mal 20 Cent, also 1200 Cent oder 12 € erwarten können.
Das Spiel lohnt sich für Ida nicht.
Was steckt dahinter? Hier kommt der Blick auf die Mathematik.
Das Spiel mit dem Glücksrad ist ein Zufallsexperiment. Das Interesse richtet sich oft auf den Gewinn (G) oder den Verlust (V). Der Verlust wird oft als negativer Gewinn bezeichnet und hat als Vorzeichen ein Minuszeichen.
Der Erwartungswert

Wird ein Zufallsexperiment durchgeführt, so nimmt eine für dieses Experiment festgelegte so genannte Zufallsgröße mit einer bestimmten Wahrscheinlichkeit p(X) einen Wert an.
Zufallsgrößen werden meist mit X, Y oder Z bezeichnet.
Die Zuordnung der Werte der Zufallsgrößen zu ihren Wahrscheinlichkeiten wird Wahrscheinlichkeitsverteilung genannt.
Der Erwartungswert E(X) der Zufallsgröße X ist der Wert, der bei der mehrfachen Durchführung eines Zufallsexperiments im Durchschnitt zu erwarten ist.
Die Berechnung erfolgt durch Multiplikation der Werte der Zufallsgröße mit ihren Wahrscheinlichkeiten und der anschließenden Addition der Ergebnisse.
In unserem Beispiel ist der Erwartungswert, also der durchschnittliche Gewinn pro Spiel 8 Cent für Tom.
Zufallsgröße:
X: Gewinn oder Verlust pro Spiel
(in Cent)
Wahrscheinlichkeitsverteilung von X:
| Wert von X (in Cent) | 50 | -20 |
| p(X) | 0,4 | 0,6 |
Erwartungswert von X:
E(X) = 50 $$*$$ 0,4 + (-20) $$*$$ 0,6 = 8
Abzocke am Spielautomat

Ein Spielautomatenbesitzer wirbt bei einem Einsatz von 1 € pro Spiel mit nachfolgendem Gewinnplan. Mathematisch ist das die Wahrscheinlichkeitsverteilung :
| Gewinn in € | 0 | 0,10 | 0,30 | 1,50 |
|---|---|---|---|---|
| Wahrscheinlichkeit | 0,3 | 0,4 | 0,2 | 0,1 |
Was meinst du? Ist das ein faires Spiel? Berechne dazu den Erwartungswert:
Zufallsgröße X: Gewinn bzw. Verlust pro Spiel
Erwartungswert von X:
E(X) = 0 $$*$$ 0,3 + 0,10 $$*$$ 0,4 + 0,30 $$*$$ 0,2 + 1,50 $$*$$ 0,1 = 0,25
Bei dem Einsatz von 1 € pro Spiel ist der Erwartungswert, also der durchschnittliche Gewinn 25 Cent. Der Besitzer gewinnt damit pro Spiel etwa 75 Cent. Ein solches Spiel ist nicht fair, es ist reine Abzocke - hüte dich vor solchen Spielautomaten.
Jedes Los gewinnt!
Auf einer Wohltätigkeitsveranstaltung, an der 100 Personen teilnehmen, kauft jeder Teilnehmer ein Los. Der erste Preis beträgt 200 €, der zweite Preis 100 € und der dritte Preis 50 €. Die restlichen Preise betragen 1 €.
Berechne den Erwartungswert.
Zufallsgröße X: Gewinn
Wahrscheinlichkeitsverteilung:
| Zufallsgröße X | 200 | 100 | 50 | 1 |
|---|---|---|---|---|
| p(X) | $$1/100$$ | $$1/100$$ | $$1/100$$ | $$97/100$$ |
Erwartungswert: $$E(X) = 200 * 1/100 + 100 * 1/100 + 50 * 1/100 + 1 * 97/100 = 4,47$$
Der durchschnittliche Gewinn beträgt pro Los 4,47 €. Der Veranstalter müsste einen Lospreis von 4,47 € verlangen, damit die Kosten gedeckt sind. Der Losverkauf dient einem guten Zweck. Er wird deutlich mehr verlangen und den Gewinn diesem Zweck zuführen.
Bei einem Lospreis von 10 € und 100 verkauften Losen entsteht z.B. ein Gewinn von (10 €$$-$$4,47€) $$*$$100 = 553 €.
Urnenexperiment als Glücksspiel
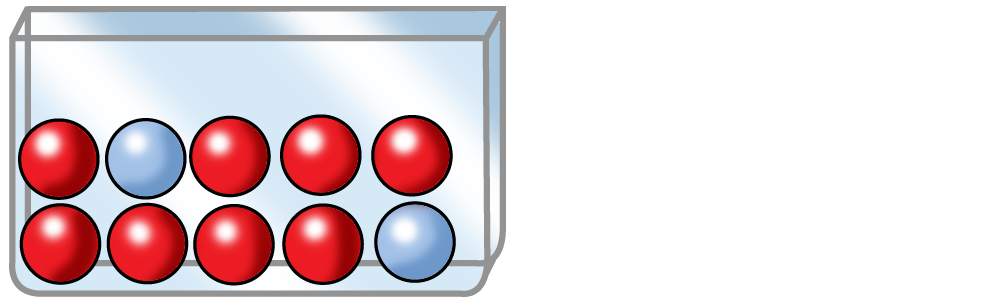
Eine Urne enthält 8 rote (R) Kugeln und 2 blaue (B) Kugeln. Zieht Tom eine blaue Kugel, gewinnt er 10 €. Sein Einsatz beträgt 5 €. Lohnt sich dieses Spiel für Tom?
Berechne den Erwartungswert des Gewinns von Tom pro Spiel.
Zufallsgröße X: Gewinn / Verlust pro Spiel
Wahrscheinlichkeitsverteilung :
| X | 10 | -5 |
|---|---|---|
| p(X) | $$2/10 = 1/5$$ | $$8/10 = 4/5$$ |
Erwartungswert:
$$E(X) = 10 * 1/5 + (-5) * 4/5 = 10/5 - 20/5 = -10/5 = -2$$
Der Erwarungswert ist negativ. Tom verliert pro Spiel 2 €.
Ein Spiel mit E(X) < 0 - aber auch mit E(X) > 0 - nennt man unfair.
Bei einem Einsatz von 2,50 € folgt ein Erwartungswert von $$E(X) = 10 * 1/5 + (-2,50) * 4/5 = 10/5 - 10/5 = 0$$
Ist E(X) = 0, so wird ein solches Spiel als fair bezeichnet.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen


