Anwendungsaufgaben mit Zufallsexperimenten
Argumentieren
Mathe ist mehr als Rechnen. Hier siehst du ein paar Beispiele, wie du mit Mathe argumentierst und Anwendungsaufgaben löst.
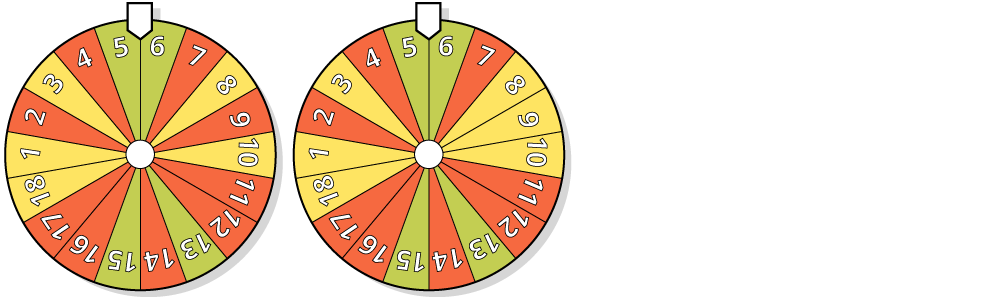 Für welches Glücksrad ist die Wahrscheinlichkeit, beim Drehen ein rotes Feld zu erhalten größer?
Für welches Glücksrad ist die Wahrscheinlichkeit, beim Drehen ein rotes Feld zu erhalten größer?
Antwort: beim linken Glücksrad
Begründung:
Die Anzahl der roten Felder im linken Glücksrad ist größer als die entsprechende Anzahl im rechten Glücksrad.
Daraus leitest du ab, dass auch die Wahrscheinlichkeit für das linke Glücksrad größer ist, beim Drehen ein rotes Feld zu erhalten.
$$p(li) = \frac{9}{18}=0,5 > p(re) = \frac{8}{18}approx0,44$$
Modellierung
Nach einer Wahl zum Schulsprecher wurden 160 Schülerinnen und Schüler befragt, wen sie gewählt haben. Die Tabelle zeigt das Ergebnis der Befragung:
| Kandidaten | Tom | Sven | Ida |
|---|---|---|---|
| abs. Häufigkeit | 40 | 24 | 96 |
Welche der Modellreihe könnte bei geeigneter Beschriftung die geschilderte Anwendungssituation richtig beschreiben?
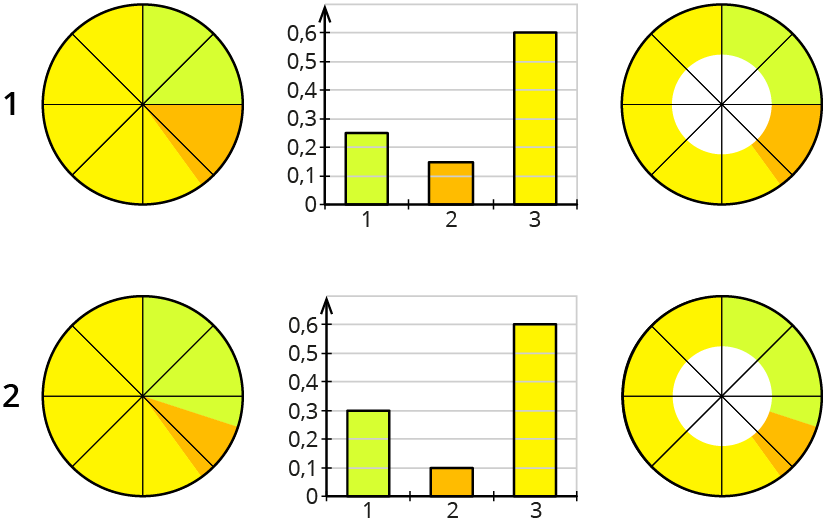
Antwort: Modellreihe 1.
Begründung:
folgt aus der Erweiterung der Tabelle und dem Vergleich mit den Modellen:
| Kandidaten | Tom | Sven | Ida |
|---|---|---|---|
| abs. Häufigkeit | 40 | 24 | 96 |
| rel. Häufigkeit | 25 % | 15 % | 60 % |
| Mittelpunktswinkel | 90° | 54° | 216° |
Modellieren
Ein mathematisches Modell besteht aus einer oder mehrerer Funktionen, Graphen, Tabellen, Gleichungen oder Ungleichungen, die eine Anwendungssituation beschreibt.
Modellierung - Fortsetzung
Hier eine allgemeine Schrittfolge, die ein richtiges Modellieren unterstützt:
Schritt 1: Aufgabe erfassen
Analysiere den Aufgabentext. Beantworte die Frage: Worum geht es?
Wenn es geht, skizziere die Anwendungssituation.
Bestimme Gegebenes und Gesuchtes.
Schritt 2: Aufgabe in die mathematische Sprache übersetzen
Lege fest, was die Variablen sind.
Übertrage gegebene Größen auf das Modell.
Stelle, falls notwendig, Gleichungen auf. Einheiten brauchst du nicht mitzuschreiben.
Schritt 3: Vergleichen - Lösen - Anpassen
Beantworte die Frage: Passt das Ergebnis zu den Aussagen des Modells? Suche Begründungen für deine Antwort.
Schritt 4: Formuliere die Antwort in einem Antwortsatz.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Ziegenproblem
 In einer Fernsehshow hat ein Kandidat die Chance ein Auto zu gewinnen, das hinter einer der drei Türen versteckt ist. Hinter den anderen beiden Türen stehen als Symbol für Niete Ziegen. Der Kandidat wählt z.B. Tür 1. Der Showmaster weiß, wo das Auto steht und öffnet Tür 3. Nun fragt er den Kandidaten, ob er bei seiner Wahl bleibt oder wechseln will.
In einer Fernsehshow hat ein Kandidat die Chance ein Auto zu gewinnen, das hinter einer der drei Türen versteckt ist. Hinter den anderen beiden Türen stehen als Symbol für Niete Ziegen. Der Kandidat wählt z.B. Tür 1. Der Showmaster weiß, wo das Auto steht und öffnet Tür 3. Nun fragt er den Kandidaten, ob er bei seiner Wahl bleibt oder wechseln will.
Wechseln lohnt sich!
Diese Aussage hat es in sich. Viele Menschen haben über das „Ziegenproblem“ nachgedacht.
Mithilfe von Spielkarten und einem Würfel könnt auch ihr das Problem lösen. Es werden Spielkarten präpariert und gewürfelt. Einer ist Showmaster und einer würfelt. Kommt eine gerade Zahl wird gewechselt, anderenfalls nicht.
In einer Tabelle werden die Ergebnisse notiert.
Hier eine Beispieltabelle für 100 Spielrunden:
| Anzahl der Gewinne beim Wechsel | 67 | 67 % |
|---|---|---|
| Anzahl der Gewinne beim Bleiben | 33 | 33 % |
Aus der Beispieltabelle könnt ihr entnehmen: Wechseln lohnt sich.
Viel Spaß beim Spielen.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen