Schriftlich dividieren

… ist gar nicht so einfach. Wenn du fit mit dem kleinen Einmaleins und der schriftlichen Subtraktion bist, wirst du das aber gut hinkriegen.

So geht’s:

Noch ein paar Beispiele zum Angucken

Beispiel: 858 $$:$$ 3

Du teilst durch eine einstellige Zahl.
Guck zuerst, wie oft die 3 in die 8 (die erste Ziffer von 858) passt. Suche die nächste Zahl kleiner als 8, die durch 3 teilbar ist. 6 $$:$$ 3 $$=$$ 2. Subtrahiere die 6 von 8.

Wie oft passt die 3 in 25? Suche die nächste Zahl kleiner als 25, die teilbar durch 3 ist. 24 $$:$$ 3 $$=$$ 8. Subtrahiere die 24 von 25.

Wie oft passt die 3 in die 18? Oh, das geht auf. 18 $$:$$ 3 $$=$$ 6.

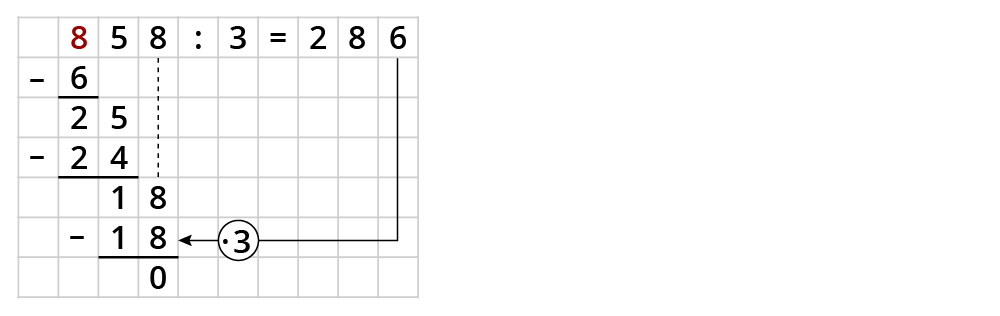
Wenn du ganz unten eine Null hast und oben keine Ziffern mehr zum Herunternehmen sind, hast du fertig gerechnet.

Mach immer eine Probe mithilfe der Multiplikation! Hier: 286 $$*$$ 3.

Die erste Ziffer ist zu klein

Beispiel: 272 $$:$$ 8

Die 8 passt überhaupt nicht in die 2. Dann nimmst du die ersten beiden Ziffern und guckst, wie oft die 8 reinpasst. Suche die nächste kleinere Zahl von 27, die durch 8 teilbar ist. Das ist 24.

Und die Probe:

Division durch eine mehrstellige Zahl

Beispiel: 3174 $$:$$ 23

Urgks, ungemütlich mit den großen Zahlen. Das Prinzip ist aber das gleiche.

Die 23 passt nicht in die 3, nimm also gleich die 31. Suche die nächstkleinere Zahl, die durch 23 teilbar ist. Das ist 23.
23 $$:$$ 23$$=$$1.

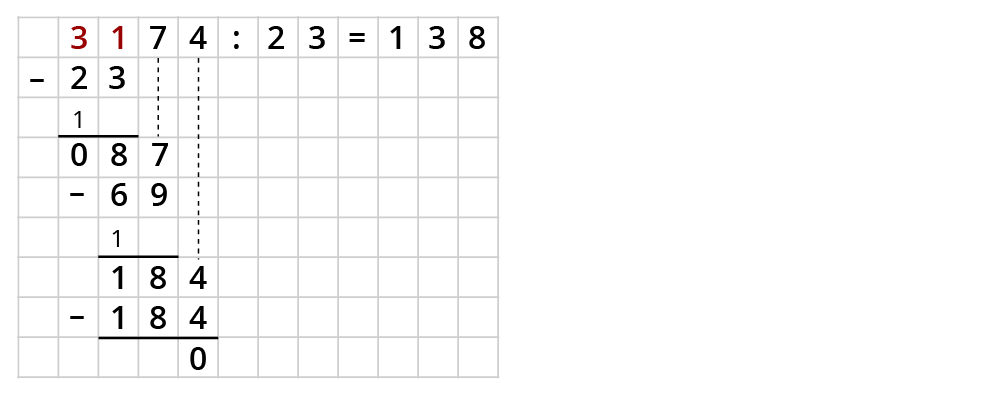
Probe nicht vergessen:

Schriftliche Division mit Rest

Bis jetzt hast du die Division bei Aufgaben durchgeführt, in denen der Divisor genau in den Dividenden gepasst hat. Das ist aber nicht immer so. Es gibt Aufgaben, da bleibt ein Rest.

Beispiel zum Einstieg:

20$$:$$6$$=$$3 Rest 2
(18 ist durch 6 teilbar. 18$$:$$6$$=$$3)

Beispiel schriftliche Division: 583 $$:$$ 7

Rechne wie immer. Aber am Schluss kommt nicht 0, sondern es bleibt eine 2 stehen.

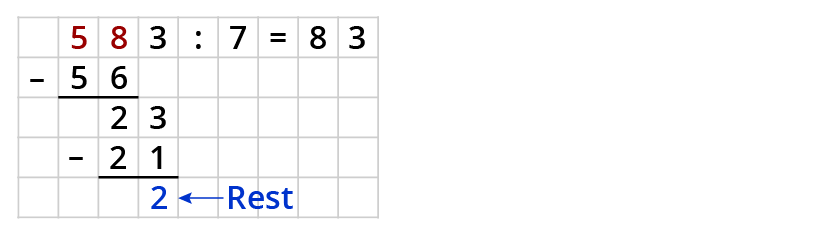
So schreibst du das Ergebnis dann auf:

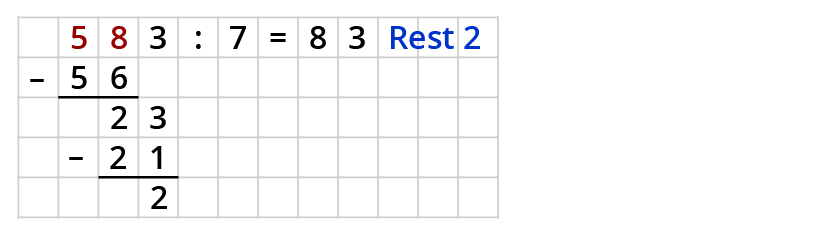
Probe:

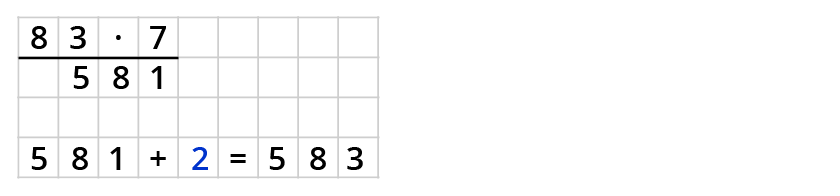
Bei der Probe multiplizierst du zuerst den Quotienten ohne Rest mit dem Divisor. Dann addierst du den Rest zum Ergebnis.