Multiplizieren und Dividieren

Reicht nicht Plus- und Minusrechnen?

Die Multiplikation ist ja schließlich eine wiederholte Addition.
5 · 4 heißt ja: 5+5+5+5.
Bei beiden Wegen kommt 20 raus.

Bei kleinen Zahlen ist egal, welchen Weg du nimmst.

Aber hier wirst du froh sein, dass es die Multiplikation gibt:
Die 29 Schüler der Klasse 5c sollen 3 € für’s Kino mitbringen. Die Klassensprecherin sammelt das Geld ein. Wie viel muss sie am Ende haben?

3 € · 29 geht viel schneller als 3+3+3+3+3+… und das 29-mal.☺

Aber es gibt auch noch viel mehr zu entdecken als „nur“ das Rechnen! Hier geht’s erst mal um natürliche Zahlen. Das sind die Zahlen, die du ganz normal zum Abzählen nimmst: 0, 1, 2, 3,… Alles andere kommt später.

Darstellung der Multiplikation

Auf dem Zahlenstrahl

Du kannst die Multiplikation am Zahlenstrahl darstellen.

Beispiel:

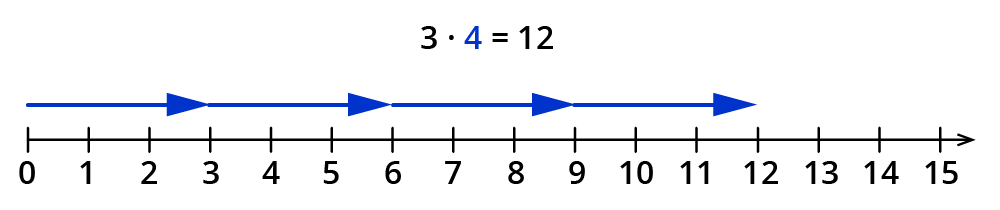
Der Multiplikationsoperator

Die Multiplikation kannst du auch mit einem Multiplikationsoperator darstellen. Dazu verwendest du Pfeile:

Beispiel:

Fachbegriffe

Die Zahlen, die multipliziert werden, heißen Faktoren und das Ergebnis einer Multiplikation heißt Produkt.

Multiplikation im Kopf

Wenn du im Kopf multiplizierst, hast du 2 Möglichkeiten.

Beispiel: $$28*4$$

1. Möglichkeit: Multipliziere erst die Zehner und dann die Einer. Addiere die Ergebnisse.

$$20*4 = 80$$

$$8*4=32$$

$$80+32=112$$

2. Möglichkeit: Du ergänzt hier den ersten Faktor auf volle Zehner und subtrahierst die Ergänzung hinterher.

$$30*4=120$$

Ergänzung: $$2*4 =8$$

$$120-8=112$$

Die Division

Bei der Division heißt das Ergebnis Quotient. Die Zahl, die zu dividieren ist, heißt Dividend. Die Zahl, durch die dividiert wird, heißt Divisor.

Der Divisionsoperator

Die Division kannst du auch mit einem Divisionsoperator darstellen. Dazu verwendest du Pfeile.

Beispiel:

Im Zusammenhang

Die Multiplikation ist die Umkehrung der Division und die Division ist die Umkehrung der Multiplikation.

Beispiele:

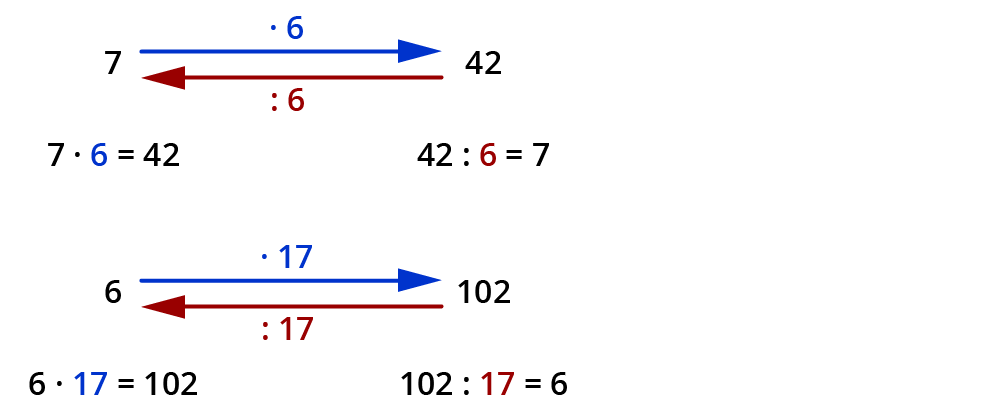
Division im Kopf

Die Division ist die schwierigste Rechenart. Da hilft nur üben, üben, üben.☺

Wenn du im Kopf dividierst, hast du 2 Möglichkeiten.

Beispiel: $$176:8$$

1. Möglichkeit: Suche eine runde Zahl kleiner als 176, die durch 8 teilbar ist. Teile den Rest auch durch 8 und addiere die Ergebnisse.

$$80:8 =10$$

Noch besser: $$160$$

$$160:8 = 20$$

$$176-160=16$$

$$16:8=2$$

$$20+2=22$$

Also: $$176:8 =22$$

2. Möglichkeit: Du ergänzt die erste Zahl zu einer runden Zahl, die durch 8 teilbar ist. Teile die Ergänzung auch durch 8 und ziehe das Ergebnis vom ersten Ergebnis ab.

$$240:8=30$$

Ergänzung: $$240-176=64$$

$$64:8=8$$

$$30-8=22$$

Also: $$176:8=22$$

Die Null

Die Null ist eine besondere Zahl. Da gibt es ein paar Regeln, die du immer wieder brauchst.

Multiplikation

Multiplizierst du eine Zahl mit 0, kommt als Ergebnis 0 raus.
$$25*0=0$$
Mathematisch ausgedrückt: Ist ein Faktor gleich Null, so ist das Produkt gleich Null.

Division

• Null geteilt durch irgendwas ist immer Null.
  
  $$0:25=0$$
  (Wenn du nichts auf 25 Leute verteilst, bekommt jeder nichts.)
  
  Oder prüfe mit der Umkehroperation:
  $$0*25$$ ist ja gleich Null. Das passt.

• Durch „Null“ kannst du nicht dividieren!
  
  Wieso nicht?
  Probier’s aus: Was könnte bei $$34 : 0$$ rauskommen?
  
  Angenommen, $$34:0=0$$, dann muss die Umkehrung gelten: $$0*0=34$$. Das kann nicht sein. Bei $$22:0=0$$ müsste dann $$0*0=22$$ sein. Das geht nicht.
  
  Angenommen, $$34:0=34$$, dann muss die Umkehrung gelten: $$34*0=34$$. Das widerspricht der Regel oben, dass irgendwas mal 0 gleich 0 ist. Geht auch nicht.
  
  Mathematiker sagen: Die Division durch 0 ist nicht definiert. Du kannst dir merken, dass die Division durch 0 nicht möglich ist.