Vermischte Aufgaben mit Flächen
Flächen
Flächen kennst du sicher aus deinem täglichen Leben in vielen Bereichen. Etwa die Fläche deine Zimmers in $$m^2$$ oder die Größe eines Fußballplatzes in $$ha$$, oder?
 Bild: iStockphoto.com (gerenme ); iStockphoto.com/Aksonov, Dmytro
Bild: iStockphoto.com (gerenme ); iStockphoto.com/Aksonov, Dmytro
In dieser Lerneinheit geht es um etwas kompliziertere Aufgaben, bei denen du manchmal auch Wissen aus anderen mathematischen Bereichen anwenden musst. Das kann zum Beispiel der Satz des Pythagoras sein, der Strahlensatz oder sogar der Sinus.
Aber keine Panik: Sollte das der Fall sein, bekommst du in den Aufgaben Hinweise dazu!
Das weißt du bestimmt noch:
$$1 $$ $$cm^2$$ $$ =100$$ $$mm^2$$
$$1 $$ $$dm^2$$ $$=100$$ $$cm^2$$
$$1 $$ $$m^2$$ $$=$$ $$100$$ $$dm^2$$ $$= 10000$$ $$cm^2$$
$$1$$ $$a$$ $$= 100$$ $$m^2$$
$$1 $$ $$ha$$ $$= 100$$ $$a$$ $$= 10000$$ $$m^2$$
$$1 $$ $$km^2$$ $$= 100$$ $$ha$$
Grundwissen und Formeln
Hier sind die wichtigsten Formeln für Flächeninhalte. Die kennst du bestimmt (fast) alle:
| Figur und Formel | Grafik |
|---|---|
| Quadrat $$A=a*a$$ | 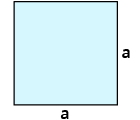 |
| Rechteck $$A=a*b$$ | 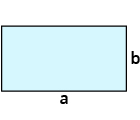 |
| Dreieck $$A=(g*h)/2$$ | 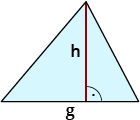 |
| Parallelogramm $$A=g*h$$ | 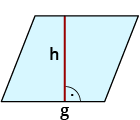 |
| Trapez $$A=(a+c)/2*h$$ | 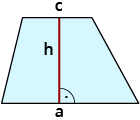 |
Das Formelzeichen für eine Fläche ist $$A$$ und kommt vom englischen $$area$$ (=Fläche).
Noch mehr Formeln
Jetzt geht es rund!
| Figur und Formel | Grafik |
|---|---|
| Kreis $$A=pi*r^2$$ | 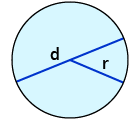 |
| Kreisring $$A_(KR)=pi*(r_a^2-r_i^2)$$ | 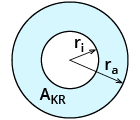 |
| Kreisausschnitt $$A_(KA)=pi*r^2*alpha/360$$ | 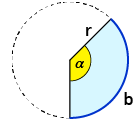 |
Einige Flächengrößen:
Dicker Bleistiftpunkt: $$1$$ $$mm^2$$
Kleiner Fingernagel: $$1$$ $$cm^2$$
Innenfläche Hand: $$1$$ $$dm^2$$
Tür / Singlebett: $$2$$ $$m^2$$
- Tennisplatz (Einzel): $$2$$ $$a$$
- Fußballplatz:$$0,7$$ $$ha$$
- Insel Neuwerk: $$3$$ $$km^2$$
Die Oberfläche von Körpern
| Körper und Formel | Grafik |
|---|---|
| Quader $$O=2ab+2ac+2bc$$ (Würfel $$O=6a^2$$) | 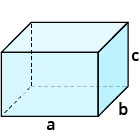 |
| Zylinder $$O=2*pi*r^2$$ $$+2*pi*r*h_k$$ | 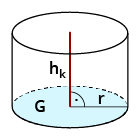 |
| Pyramide $$O=a^2+2*a*h_a$$ | 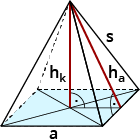 |
| Kegel $$O=pi*r^2+pi*s*r$$ | 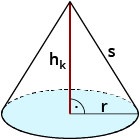 |
| Kugel $$O=4*pi*r^2$$ | 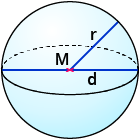 |
Das Formelzeichen für die Oberfläche eines Körpers ist das $$O$$.
So gehst du beim Rechnen vor
Vier Schritte fürs Lösen einer Aufgabe:
- Aufgabe erfassen: Was wird gesucht, was ist gegeben? Skizze anfertigen!
- Gleichung aufstellen. Einheiten weg!
- Gleichung lösen.
- Checken, ob die Lösung Sinn macht!
Tipps und Tricks
Bei allen geometrischen Aufgaben solltest du immer eine Zeichnung anlegen. Diese muss auch nicht besonders sauber aussehen (außer in Klassenarbeiten).
Wenn du Probleme beim Umformen einer Gleichung hast, ist es oft sinnvoll, die Aufgabe mit ganz einfachen Zahlen zu rechnen. Dann weißt du meistens, was zu tun ist.
Vertraue nie blind dem Ergebnis des Taschenrechners. Überlege dir, ob dein Ergebnis sinnvoll ist und zur Aufgabenstellung passt.
Beispiel: Es kann nicht sein, dass deine Körperoberfläche $$O = 2 ha$$ ist, dann wärst du ja größer als ein Fußballplatz!
Eine gerechnete Beispielaufgabe
Aus einem quadratischen Stück Blech der Größe $$20$$ x $$20 $$ $$cm^2$$ werden vier Kreise wie auf dem Bild ausgestanzt.
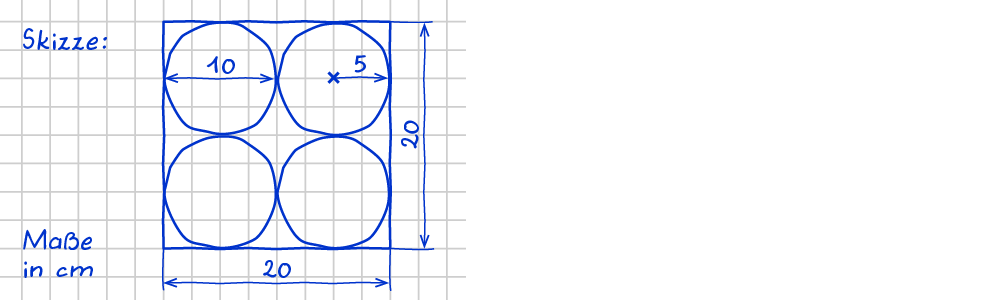
Wie viel Prozent beträgt der Abfall an dem Stück Fläche?
Runde auf Ganze.
1. Aufgabe erfassen: Was wird gesucht, was ist gegeben? Skizze anfertigen!
Gesucht:
Fläche außerhalb der vier Kreise.Gegeben:
Seitenlänge des Quadrats: $$a=20$$ $$cm$$
Die Seitenlänge des Quadrats verrät uns direkt den Flächeninhalt des Quadrats:
$$A_Q=a^2=20$$ $$cm^2=400$$ $$cm^2$$
2. Gleichung aufstellen. Einheiten weg!
Die Seitenlänge des Quadrats enstspricht 2 mal dem Durchmesser des Kreises, also viermal dem Radius:
$$20=4*r$$Fläche der Kreise:
1 Kreis: $$A_K=pi*r^2$$
4 Kreise: $$A_(4K)=4* pi*r^2$$gesuchte Fläche: $$A=A_Q-A_(4K)=400-A_(4K)$$
3. Gleichung lösen.
Aus $$20=4*r$$ folgt $$r=5$$
einsetzen in die Formeln:
$$A_(4K)=4* pi*r^2$$
$$A_(4K)=4* pi*5^2=4* pi*25 approx 314,16$$
$$A=400-A_(4K)=400-314,16=85,84$$
4. Checken, ob die Lösung Sinn macht!
$$85,84/400=0,2146=21,46%$$
$$85,84$$ entspricht etwa einem Fünftel der Quadratfläche ($$400$$). Schauen wir uns die Skizze an, kommt es ungefähr hin.
Antwortsatz: Der Abfall an dem Stück beträgt $$21,46%$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



