Vektoren
Vektoren
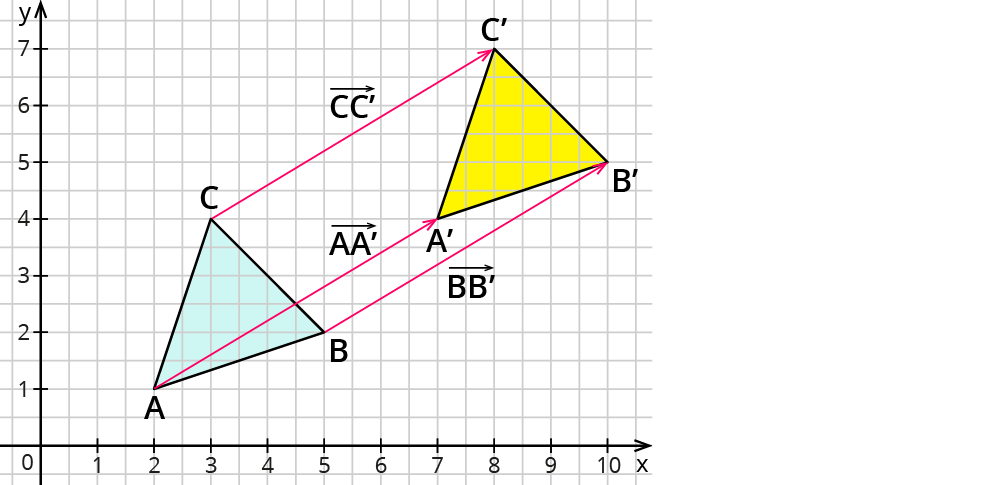
Du siehst im Bild ein Dreieck, bei dem die Eckpunkte durch Pfeile ein Stückchen verschoben wurden. Hast Du Dich schon einmal gefragt, wie diese Verschiebungspfeile eigentlich bezeichnet werden?
Von Pfeilen und Vertretern
Die Abbildung zeigt eine Parallelverschiebung des Dreiecks $$ABC$$ zum Dreieck $$A’B’C’$$. Zu dieser Verschiebung gehört eine Menge paralleler, gleich langer und gleich gerichteter Pfeile. Würdest Du die Pfeile übereinander legen, wäre nur noch ein Pfeil zu sehen.
Dieser Pfeil (der eigentlich eine ganze Menge von Pfeilen bezeichnet!) heißt Vektor $$vec v$$.
Es gilt also $$vec v ={vec{\A\A’}, vec{BB’}, vec{\C\C’},…}$$
Der Vektor $$vec v$$ ist somit eine Abkürzung für eine Menge von gleichgearteten Verschiebungspfeilen!
Um den Vektor darzustellen, greifst Du Dir nun einfach einen Pfeil dieser großen Menge, z.B. $$vec {\A\A’}$$, heraus. Dieser Pfeil heißt Repräsentant oder auch Vertreter des Vektors $$vec v$$, oder eben einfach nur „Vektor $$vec {\A\A’}$$“.
Eigenschaften eines Vektors
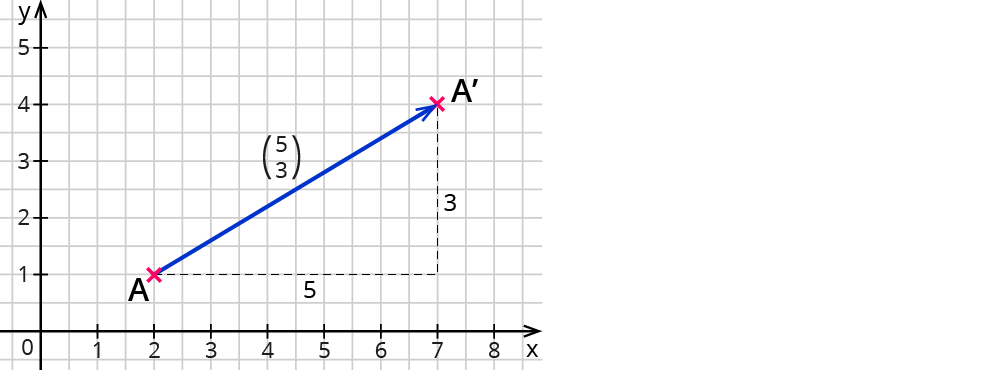
Die Länge und die Richtung des Vektors $$vec {\A\A’}$$ lässt sich einfach mit Hilfe des Koordinatensystems darstellen. Du weißt schon, dass eine Verschiebung in der Ebene einen Punkt $$A$$ auf den Punkt $$A’$$ abbildet - genau das gibt der Vektor auch an!
Du erhältst z.B. den Vektor $$vec {\A\A’}$$, indem du vom Punkt $$A(2|1)$$ aus
5 Einheiten nach rechts und 3 Einheiten nach oben
gehst. So kommst du zum Punkt $$A’(7|4)$$. Damit wird Punkt $$A$$ auf Punkt $$A’$$ abgebildet!
Um eine kürzere Schreibweise zu erhalten, schreiben Mathematiker diese Angaben als ein Zahlenpaar der Form:
$$((5),(3))$$ (lies einfach „5 3“).
Die erste Zahl heißt auch $$x$$-Koordinate, die zweite Zahl $$y$$-Koordinate des Vektors $$vec v$$. Du kannst also jeden Vektor in der Ebene schreiben als
$$vec v = ((v_x),(v_y))$$,
Die Zahlen $$v_x$$ und $$v_y$$ heißen die Koordinaten des Vektors $$vec v$$.
Koordinaten mit Minuszeichen
Natürlich läuft ein Pfeil nicht immer von links unten nach rechts oben, sondern kann in verschiedene Richtungen zeigen.
Zeigt ein Pfeil bzw. Vektor nach links oder nach unten, so wird dies durch ein Minuszeichen markiert.
Dabei gibt die obere Zahl eine Verschiebung nach rechts (+) oder links (–) und die untere Zahl eine Verschiebung nach oben (+) oder nach unten (–) an.
Beispiele:
$$((-5),(3))$$ 5 Einheiten nach links, 3 nach oben
$$((5),(-3))$$ 5 Einheiten nach rechts, 3 nach unten
$$((-5),(-3))$$ 5 Einheiten nach links, 3 nach unten.
Beachte, dass das Pluszeichen als Vorzeichen in der Mathematik in der Regel nicht notiert wird - als Rechenzeichen muss es notiert werden.
Hier siehst du vier Vektoren mit unterschiedlichen Vorzeichen der Koordinaten: 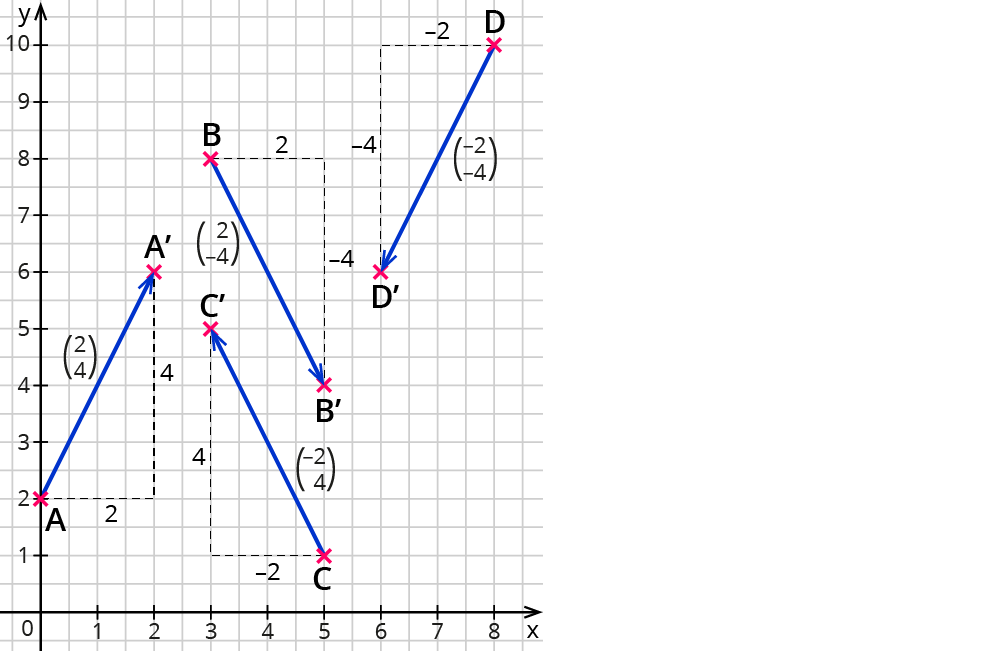

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Ablesen von Vektoren
Wenn du die Koordinaten der Vektoren bestimmen sollst, musst du nachzählen, wie viele Längeneinheiten du von einem Punkt ausgehend nach rechts/links bzw. oben/unten gehen musst, um zu den entsprechenden Bildpunkten zu gelangen.
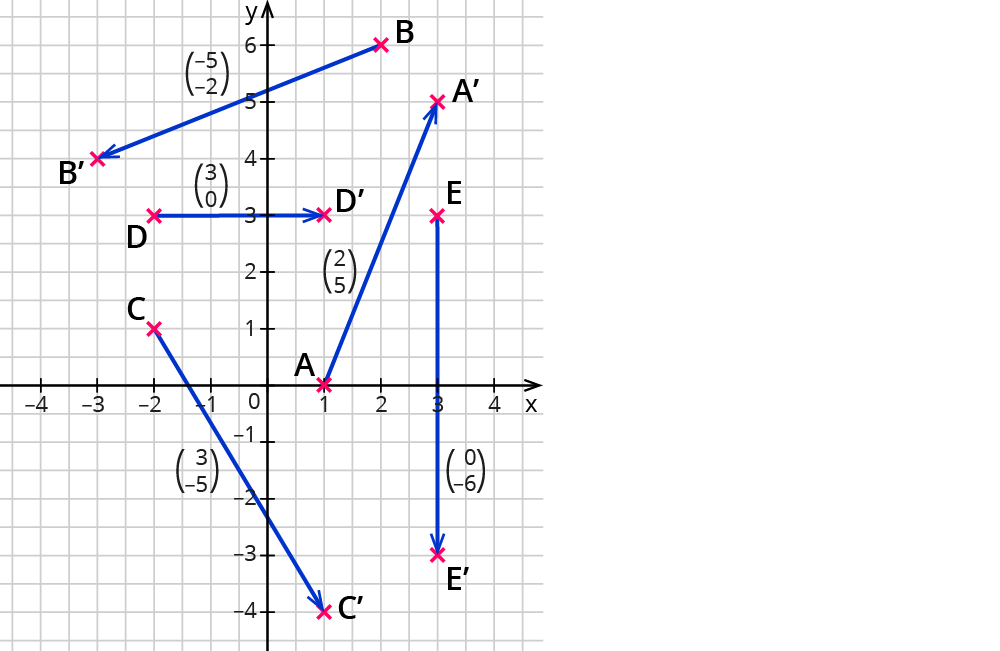
In dem Beispiel geht ein Pfeil von $$A$$ nach $$A’$$, und zwar 2 Einheiten nach rechts und 5 Einheiten nach oben, also
$$vec{A A’}=((2),(5))$$.
Kommst du auch bei den anderen Vektoren auf die richtigen Werte?
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



