Kongruenzabbildungen mithilfe von Vektoren
Sind die Dreiecke kongruent?
Dreiecke sind kongruent, wenn sie deckungsgleich sind.
Sie stimmen dann in Form und Größe überein.
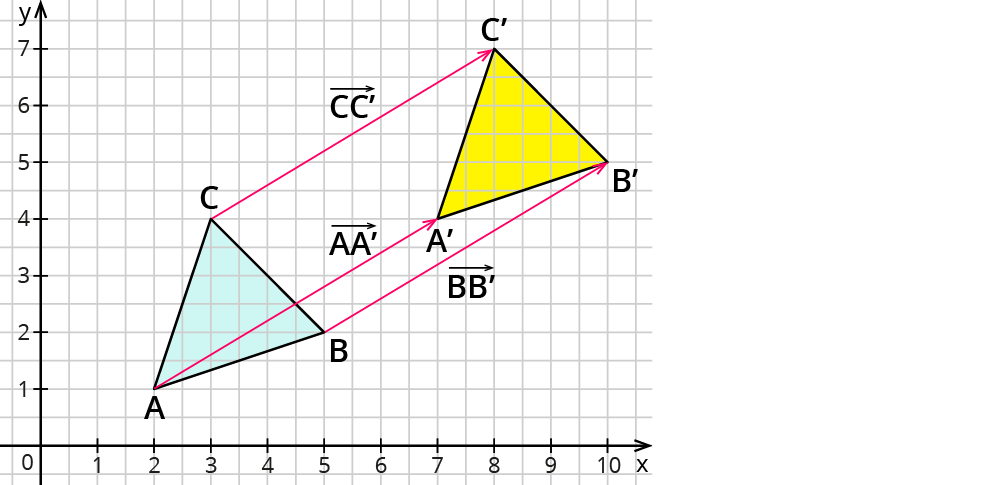
Untersuchung der Dreiecke $$ABC$$ und $$A’B’C’$$
Es gibt verschiedene Möglichkeiten herauszufinden, ob Dreiecke kongruent zueinander sind. Eine Möglichkeit ist, sich die Verschiebungspfeile $$vec {\A\A’}, vec {BB’}, vec {\C\C’}$$ anzuschauen:
$$vec {\A\A’} = ((5-2),(3-1))=((3),(2))$$, $$vec {\B\B’} = ((8-5),(4-2))=((3),(2))$$ und
$$vec {\C\C’} = ((6-3),(5-3))=((3),(2))$$.
Alle drei Verschiebungspfeile haben dieselben Koordinaten, sind also Repräsentanten des Vektors $$vec v=((3),(2))$$. Dreieck $$A’B’C’$$ ist somit aus dem Dreieck $$ABC$$ durch eine Verschiebung hervorgegangen. Da eine Verschiebung eine Kongruenzabbildung ist, sind die Dreiecke kongruent.
In Kurzform folgt: $$ Delta ABC ~=Delta A’B’C’$$.
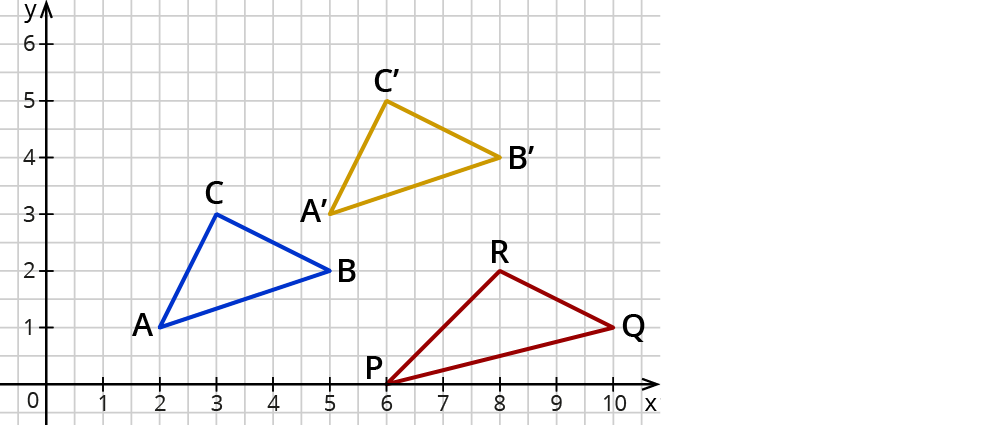
Untersuchung der Dreiecke $$ABC$$ und $$PQR$$
Hier haben die Verschiebungspfeile die Koordinaten
$$vec {\AP} = ((6-2),(0-1))=((4),(-1))$$, $$vec {BQ} = ((10-5),(1-2))=((5),(-1))$$ und
$$vec {CR} = ((8-3),(2-3))=((5),(-1))$$.
Du siehst sofort, dass die drei Verschiebungspfeile hier nicht gleich sind. Außerdem kannst Du erkennen, dass die Seitenlängen von $$[AB]$$ und $$[PQ]$$ unterschiedlich sind. Die Dreiecke $$ABC$$ und $$PQR$$ sind also nicht deckungsgleich und somit nicht kongruent.
Kongruenz und Vektoren
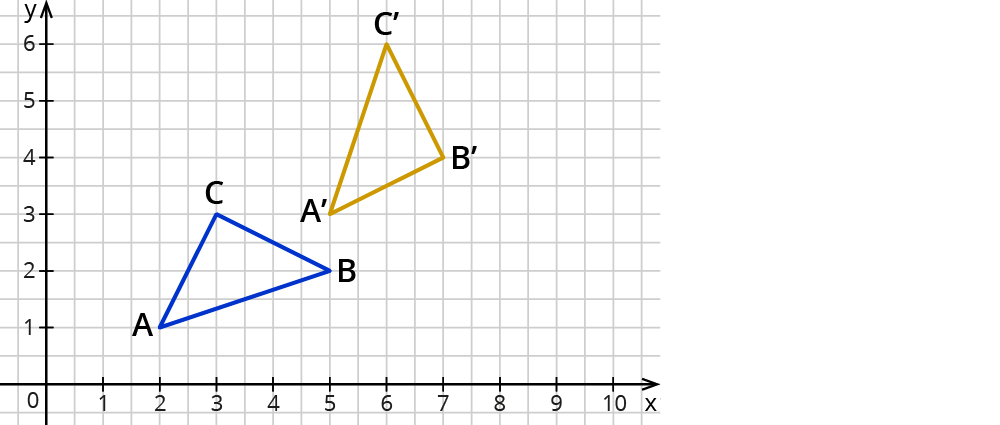
Reicht es auch aus, sich nur die Verschiebungspfeile anzuschauen, um eine Kongruenzabbildung zu erkennen? Schau dir dazu die zwei Dreiecke in der Abbildung an.
Berechnest du die Verschiebungspfeile $$vec {\A\A’}, vec {BB’}, vec {\C\C’}$$, erhältst du folgendes Ergebnis:
$$vec {\A\A’} = ((5-2),(3-1))=((3),(2))$$, $$vec {\B\B’} = ((7-5),(4-2))=((2),(2))$$ und
$$vec {\C\C’} = ((6-3),(6-3))=((3),(3))$$.
Es entstehen drei unterschiedliche Verschiebungspfeile.
Ist damit gezeigt, dass die beiden Dreiecke nicht kongruent sind?
Vergleiche die Seitenlängen der Dreiecke. Was vermutest du?
Richtig: Da alle drei Seitenlängen übereinstimmen, sind die Dreiecke nach dem Kongruenzsatz SSS kongruent!
Parallele und gleich lange Strecken
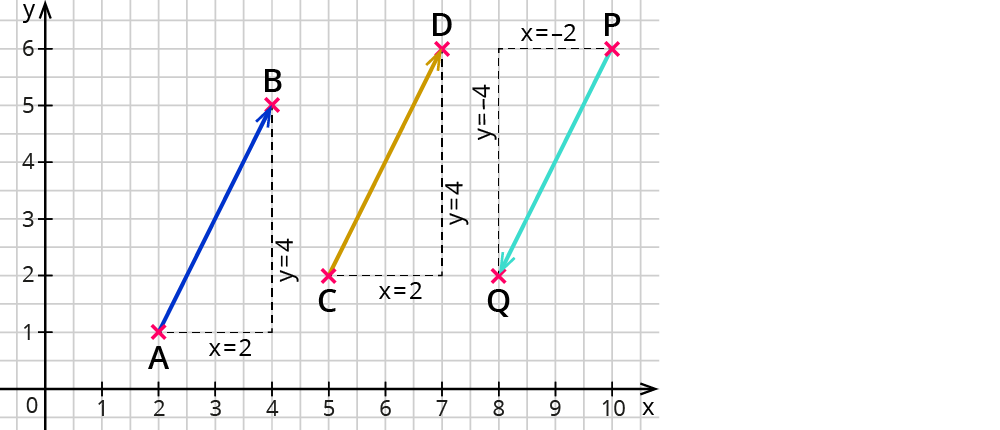
Du kannst Vektoren auch dazu benutzen, Strecken miteinander zu vergleichen. Wie kannst du hier Ähnlichkeiten erkennen?
Beispiel
Die Abbildung zeigt drei gleich lange Strecken, die parallel zueinander verlaufen. Die zugehörigen Vektoren lauten:
$$vec {\AB} = ((4-2),(5-1))=((2),(4))$$ , $$vec {\CD} = ((7-5),(6-2))=((2),(4))$$ und
$$vec {PQ} = ((8-10),(1-5))=((-2),(-4))$$.
Die Vektoren $$vec {\AB}$$ und $$vec {\CD}$$ haben die gleichen Koordinaten , hier $$vec {\AB} = ((2),(4)) = vec {\CD}$$. Sie repräsentieren denselben Vektor und sind somit gleichlang und parallel.
Was ist mit dem Vektor $$vec {PQ}$$? Genau: er ist der Gegenvektor sowohl zu $$vec {\AB}$$ als auch zu $$vec {\CD}$$. Damit zeigt er zwar in die andere Richtung, ist aber trotzdem parallel und gleichlang!
Zwei Strecken $$[AB]$$ und $$[CD]$$ bzw. $$[AB]$$ und $$[PQ]$$ sind gleich lang und verlaufen parallel zueinander, wenn ihre zugehörigen Vektoren entweder die gleichen Koordinaten besitzen oder entgegengesetzte Vorzeichen aufweisen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Gleich lange Strecken
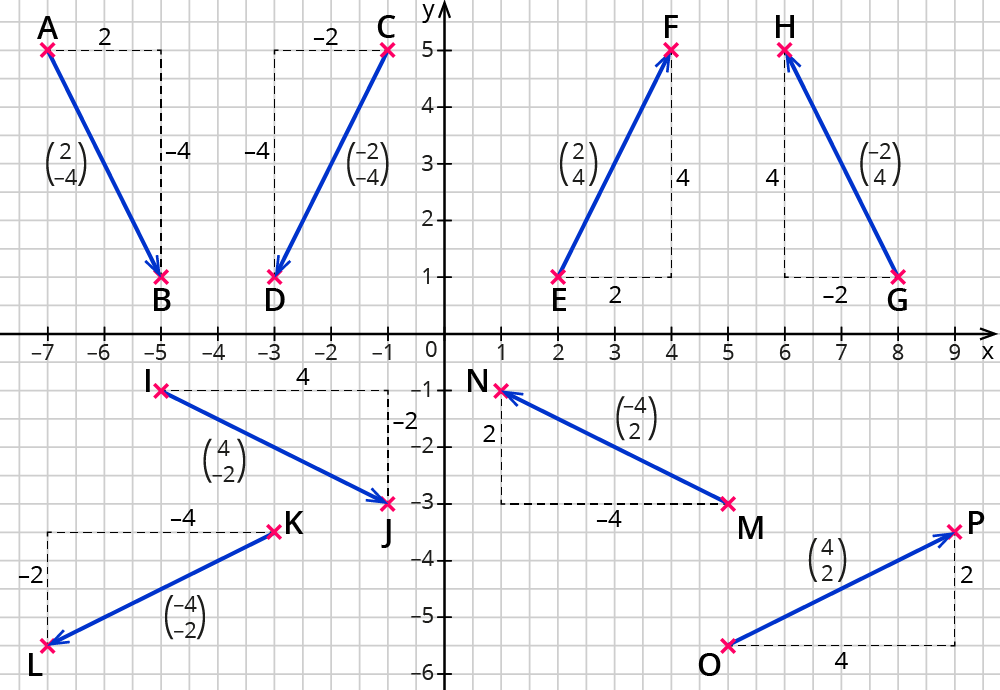
Die Abbildung zeigt acht verschiedene Vektoren. Welche Gemeinsamkeiten fallen Dir auf?
- Die Vektoren scheinen alle gleichlang zu sein.
- In den Koordinaten kommt immer die $$2$$ und $$4$$ vor, in verschiedener Reihenfolge und unterschiedlichem Vorzeichen.
Das ist kein Zufall: Du verschiebst hier jeden Vektor einmal um zwei Einheiten und einmal um vier Einheiten, also um die gleiche Strecke. Somit sind alle diese Vektoren tatsächlich gleich lang!
Dieses Ergebnis kannst du auch verallgemeinern:
Wenn die Koordinaten zweier Vektoren ohne Berücksichtigung der Vorzeichen gleich sind, dann sind die zugehörigen Strecken gleich lang.
Beispiele
Aus $$vec (RS)=((5),(-8))$$ und $$vec (PQ)=((8),(5))$$ folgt $$bar (RS) = bar(PQ)$$.
Aus $$vec (ST)=((-3),(9))$$ und $$vec (UV)=((-3),(7))$$ folgt $$bar (ST) != bar(UV)$$.
Beispiele zum Steckenvergleich

Die Abbildung zeigt wieder die acht verschiedenen Vektoren gleicher Länge. Kannst du weitere Gemeinsamkeiten finden?
Parallele und gleich lange Strecken
Einige Vektoren „passen“ genau übereinander, auch wenn sie verschiedene Koordinaten haben.
Vergleiche zum Beispiel $$vec {\AB}=((2),(-4))$$ mit $$vec {GH}=((-2),(4))$$. Da $$((2),(-4))=-((-2),(4))$$ gilt, sind $$vec {\AB}$$ und $$vec {GH}$$ Gegenvektoren zueinander. Damit sind die zugehörigen Strecken $$bar (AB)$$ und $$bar (GH)$$ gleich lang und parallel.
Welche anderen Gegenvektoren findest du außerdem?
Weitere Beispiele
Mit diesem Wissen kannst du auch parallele und gleich lange Vektoren erkennen, die nicht skizziert sind. Vergleiche den Vektor $$vec{AB}=((1),(2))$$ jeweils mit
- $$vec {CD}=((1),(-2))$$: gleich lang, aber nicht parallel.
- $$vec {EF}=((2),(-2))$$: weder gleich lang noch parallel.
- $$vec {GH}=((-1),(-2))$$: gleich lang und parallel.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen